基于PCK视角的数学原理的教学设计——以勾股定理为例

范芬瑞，韩龙淑

一、数学原理的教学有待进一步加强

数学原理是数学概念具有某种性质或者数学概念之间具有某种关系的判断，数学公式、法则、性质、公理、定理等统称为数学原理。数学原理是中学数学知识结构的核心，在数学教学中占有重要的地位。［1］

勾股定理是著名的数学定理，勾股定理在数学发展史上具有重大的意义，它的证明是论证数学的发端；勾股定理还导致了无理数的发现，拓宽了人们对数的认识。

勾股定理的教学一般在八年级,正是学生发展数学推理论证能力的重要阶段，也是具体形象思维向抽象思维过渡的时期。勾股定理的教学是难点，让学生能够在思路上比较“自然地”想到证明方法有一定的困难。［2］人教版、北师大版、苏教版三个版本的数学教材对勾股定理内容的呈现有所不同。在“一标多本”的大背景下，教师如何整合各版本教材的特色并创造性地运用教材尤为必要。以勾股定理作为数学原理的案例，从PCK的“3W+3H”视角对勾股定理的内容进行教学设计。

二、基于PCK的数学原理的教学设计思路

（一）PCK的“3W+3H”框架

学科教学知识是《中学教师专业标准》中专业知识维度的核心要素。学科教学知识（Pedagogical Content Knowledge）简称PCK，由美国学者舒尔曼首先提出，他认为PCK是教师的教学经验、学科内容知识和教育学的整合。之后格罗斯曼对PCK进行了阐释，包括：教学目的、学生经验和潜在困难、课程内容与其他内容的联系、教学策略和表征知识。［3］

教学设计包括教学内容分析、教学目标分析、学情分析、教学方法与媒体、教学过程、教学评价等，是教师PCK水平的集中反映。鉴于目前教师对“为什么教学”新内容缺乏足够的认识，致使新学习内容产生的必要性和教学价值体现不够，学生未能感悟到学习新知识的现实需要和数学需要，不易形成认知和情感的内在学习需求，本研究中把“为什么教学”单独列为PCK的一个要素，将PCK的要素梳理为六个维度，分别是教学内容的价值（Why）、教学内容（What）、教学目标（Where）、学生的现实（How）、教学策略（How）和教学评价（How），简称“3W+3H”。

（二）基于PCK的“3W+3H”视角进行勾股定理的内容解析

教学内容即教学什么（What），重在挖掘数学本质和数学学科核心素养。勾股定理是对直角三角形性质三边之间数量关系的进一步研究，可理解为勾股定理的代数意义：在直角三角形中，两条直角边的平方和等于斜边的平方。勾股定理的几何意义是：以斜边为边长的正方形的面积等于以两直角边为边长的正方形面积之和。通过勾股定理的学习培养了学生数学核心素养中的直观想象、数学抽象和逻辑推理素养。

教学目标（Where），即三维目标的整合。《义务教育数学课程标准》（2011年版）对勾股定理的教学要求是探索，即要求学生在数学活动中发现并能理性认识勾股定理。经历勾股定理的论证过程，培养合情推理和演绎推理的能力，感悟数形结合和从特殊到一般的思想，感知数学思维的严谨性。在探索活动中，培养对数学的探索精神和理性精神，体验获得结论的快乐。［4］(P34)

学生的现实（How），指学生已有的知识、经验、方法和思维基础。学生学习勾股定理之前熟悉“认识三角形”的内容，比如“在三角形中两边之和大于第三边、两边之差小于第三边”。学习勾股定理时，学生可以通过观察，动手操作和动脑思考“在特殊的三角形——直角三角形中，三边有什么特殊关系呢”来发现勾股定理。其难点是获得理性认识，激发学生的求知欲。

教学策略即如何教学（How），依据教学目标中过程性目标动词“探索”的含义为发现勾股定理并获得理性认识，因此勾股定理的教学采用启发性讲授和发现教学法等教学方法的综合，运用PPT和板书等辅助教学。教学策略包括让学生经历猜想、直观感知和推理论证过程。

教学评价即教学的如何（How），通过当堂检测、课后作业测验等评价学生对勾股定理的掌握情况和教师的教学是否达到教学目标。

三、基于PCK视角的勾股定理的教学设计

（一）创设疑难情境提出问题

从垂直于地面的电线杆上拉一条钢绳到地面，若钢绳在电线杆的固定点距离地面8m，在地面的固定点距离电线杆底部6m，那么钢绳需要多长？

通过实际问题创设疑难情境，启迪学生并分析问题。已知直角三角形中的两直角边长分别为8m和6m，求斜边的长。显然是已知直角三角形两直角边求斜边的问题。用现实问题激发了学生的学习兴趣,体现了数学知识的应用价值。这也正是PCK中教学内容的价值（Why）维度中现实需要的体现。

（二）理性探究与直观感知相结合

运用启发性提示语：从构成三角形的基本条件“两边之和大于第三边”入手，启发学生思考直角三角形作为特殊三角形其三边之间是否还有进一步的关系。研究问题时我们常常从特殊到一般，直角三角形中哪个三角形较特殊呢？自然过渡到考虑腰为1的特殊直角三角形。

结果显示，死亡凸显组中，高自尊者在职业认同及其职业行为、职业期望两个维度上均显著高于低自尊者，二者在职业承诺、职业价值观、职业情感、职业认知四个维度上无显著差异，详见表 9。

问题1：图1已知RtΔABC,∠C=90°，两直角边长为1，猜想三边之间有什么关系？

图1

引导学生根据已有知识，推出等腰直角三角形斜边上的高是斜边的一半，再利用三角形的面积相等即：，即斜边的平方等于2。

课标中勾股定理的教学目标为探索，即不仅知道勾股定理，还要知道勾股定理是怎么来的，以及与一般三角形的区别和联系并获得理性认识。要求学生通过推理对勾股定理进行发现和猜想。学生已有的知识是任意三角形中两边之和大于第三边。那么直角三角形的三边有没有其他特殊关系呢？选用简单又特殊的直角三角形——直角边为1的等腰直角三角形对勾股定理进行探究。通过计算得到该三角形斜边的平方为2，已知两直角边都为1，从而引导学生1+1=2可能是直角边平方和与斜边平方的关系。从易到难，让学生体会可以从特殊问题入手来预测一般问题。这一设计依据PCK理论中教学目标（Where）和数学自身发展需要（Why）的两个维度，再结合学生的现实（How）设计问题。

问题2：对于一般的直角三角形是否也具有这种特殊关系呢？图2中直角三角形三边的平方分别为多少？是否符合上述猜想？请数方格验证。

图2

选用直角边为2的等腰直角三角形和直角边分别为3和4的一般直角三角形，通过数方格直观感知的方法对上述猜想简单验证。同时也将“从特殊到一般”的数学思想方法贯穿于其中。这两个问题的设计是基于PCK中的教学策略（How）维度。

通过理性探究和直观感知活动，学生已经发现：直角三角形两直角边的平方和等于斜边的平方。如果用a，b和c分别表示直角三角形的两直角边和斜边，那么a2+b2=c2。

（三）分解拼补图形论证勾股定理

对于某些特殊的直角三角形可以通过数方格的方法进行验证，而面积不能补成整格的用数方格方法已经不够了，对于任意直角三角形如图3，又该如何说明其两直角边的平方和等于斜边的平方呢？由数方格方法受阻的启发使分解拼补图形的思路自然而然、水到渠成。

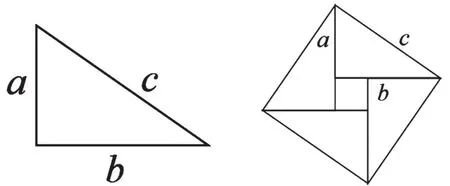
图3

引导学生受数方格的启发使用勾股弦图对勾股定理进行证明。通过计算发现：弦图中大正方形的面积等于四个全等的直角三角形面积加上小正方形的面积之和，从而推出勾股定理。这种证明方法在数方格方法的基础上更加符合课标要求，对思维层次的要求也更高。设计中渗透着数学“构造思想”和“数形结合”思想，是PCK中教学策略（How）的体现。

（四）回到问题情境，解决实际问题

数学新知识的产生源于情境，最终还要回到情境。学生根据勾股定理求钢索的长度的过程既是对新学内容的巩固，也是对学生勾股定理掌握程度的检测。这一过程正是体现了PCK中的应用价值。

（五）巩固强化把握数学原理的本质

问题3：在RtΔABC中,∠C=90°,∠A,∠B,∠C,的对边分别为 a，b，c 已知a=6,b=8.求 c；已知b=15,c=25.求a；已知a=3,c=9.求b。

问题4：如图4，图中的三角形全部是直角三角形，四边形全部是正方形，其中最大的正方形的边长是7cm,请计算A，B，C，D四个正方形的面积之和是多少？

图4

设计问题3强化对勾股定理的理解，问题4考查勾股定理的几何意义。在学生探究并证明勾股定理之后，及时巩固强化对勾股定理本质属性的理解。这是教学评价即教学的如何（How）的设计。

（六）形成系统化的知识结构网络

学习过程是学生原有认知结构中的有关知识与新学习内容相互作用，形成新的认知结构的过程，因此数学教学要使学生形成组织良好的数学认知结构。回顾本节课学习的主要内容并进行系统归纳，重在引导学生构建数学知识结构网络体系（如图5所示）。有利于完善学生的数学思维品质。

依据PCK的“3W+3H”框架对勾股定理进行教学设计，旨在说明数学原理的教学设计仅仅凭经验远远不够，需要一定的理论基础并有意识地运用其指导教学设计。教师运用PCK理论指导数学教学设计时应注意：对PCK的“3W+3H”核心要素的分析要全面与透彻，增加对数学新知识产生的必要性的分析与设计、突出数学问题的本质、注重构建数学知识结构网络等，从而激发学生数学学习的情感，丰富学生的数学认知结构网络，使学生拥有数学的眼光，学会数学思考，提升数学核心素养。

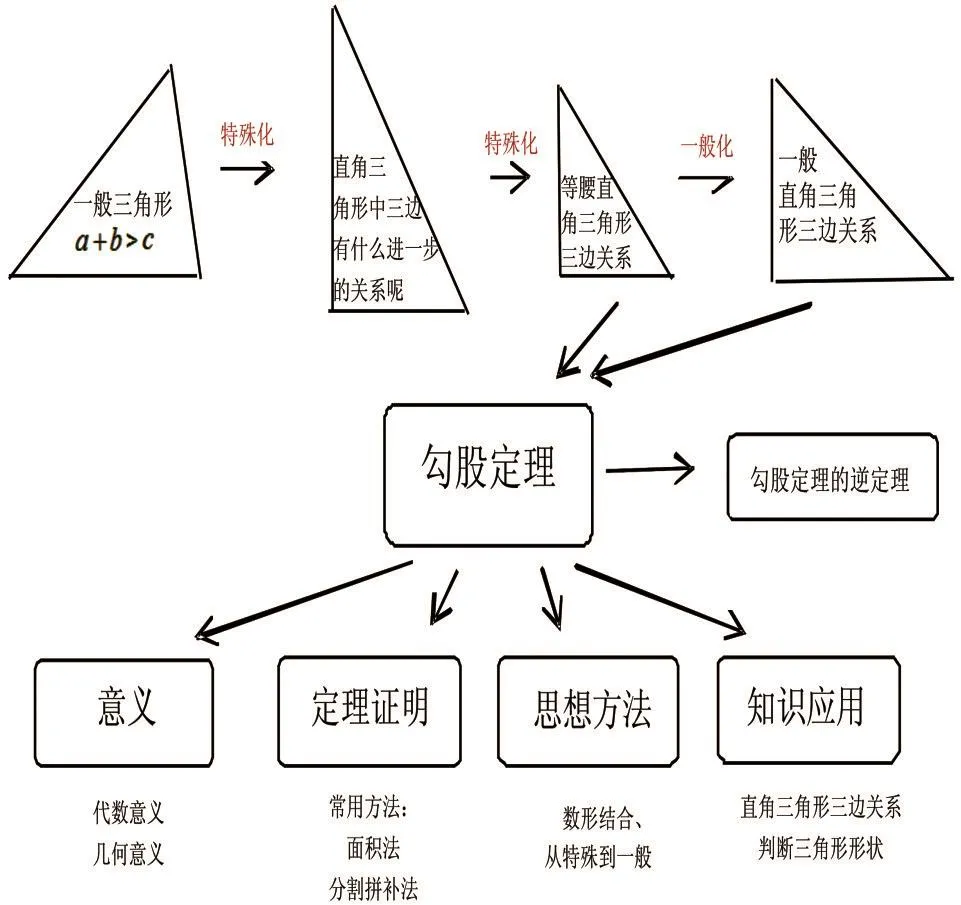
图5 勾股定理知识结构网络体系图