基于安全概略的可撤销掌纹模板生成算法

李亚楠，张雪锋

西安邮电大学 通信与信息工程学院，西安 710061

1 引言

随着全球经济和信息技术的飞速发展，信息安全逐渐被人们所关注，越来越多的领域需要进行身份认证。传统的身份认证方法在性能与安全方面有一定的局限性，已经很难满足认证系统的需求。指纹、掌纹、虹膜和人脸等这些人类所特有的生物特征开始被人们所研究，生物特征识别技术得到了良好的发展。然而在实际应用中，生物特征识别技术也暴露出了其固有的一些缺点，比如生物特征模板的丢失，虚假生物特征的攻击等[1]。因此，基于生物特征模板的身份认证方法在安全性上有待进一步改进。

近年来，可撤销的生物特征模板匹配技术取得了一定的成果[2-3]。可撤销生物特征模板匹配技术的基本思路是对生物特征进行单向不可逆变换，在生物特征模板丢失的情况下，可以通过不同的变换或者秘钥参数生成新的生物特征模板，从而有效地保护用户的生物特征信息。生物特征可撤销模板保护算法应满足以下要求[4]：

（1）多样性：同一个生物特征在不同的系统中可以生成不同的模板，并且各个模板之间，以及模板与原始生物特征之间不能相互匹配。

（2）可撤销性：在生物特征模板丢失的情况下，可以通过采用不同的变换或者秘钥参数，重新生成一个不同的模板。

（3）不可逆性：任何条件下均不能通过生物特征模板恢复出原始的生物特征信息。

（4）精确性：满足以上三个条件的基于生物特征的身份认证性能能够满足信息系统对安全性、识别率等性能需求。

在众多的生物特征中，掌纹因纹理信息丰富、识别精度高、用户可接受性强等特性，已经引起了研究者们的广泛关注[5]。针对基于掌纹的可撤销模板生成技术的研究，目前已取得了一些成果。Ratha等[6]利用不可逆变换首次引入了可撤销生物特征的概念。Goh等[7]提出了BioHashing算法，通过用户令牌生成的辅助数据与生物特征进行融合生成可撤销模板，在令牌安全的情况下取得了等错误率（Equal Error Rate，EER）为0的识别效果。Kong等[8]解释了BioHashing中EER之所以能达到0的理想值是因为用户令牌的随机化，不同的令牌增大了用户的类间距离。而且当令牌被盗时识别性能会有大幅的下降，甚至倒不如普通的生物认证方法有效。事实上，在令牌泄露且不进行阈值量化的情况下，BioHashing相当于随机映射算法[9]，很难达到理想的识别率。Teoh等[10]将BioHashing思想应用于掌纹的识别当中，提出了PalmHashing算法，但该算法同样依赖于令牌的安全性，在令牌丢失后也很难达到很好的认证性能。Leng等[11]通过对Gabor滤波器参数随机化处理生成了随机Palm Code，但此方案与Palm Code[12]相比，在认证性能上并没有很大的提高。随后，Leng等[13]采用Gabor滤波器多方向分数级融合的思想提出了识别精度更高的Palm-Phasor算法，并对其进行了理论分析[14]，但该算法的计算复杂度较高。文献[15]将掌纹图像投影到一个随机矩阵中，使图像的像素值发生不可逆变换，将投影后图像的特征向量作为掌纹模板。虽然该算法有良好的认证性能，但是安全性依赖于随机矩阵。文献[16]提出一种适用于掌纹的可撤销模糊金库（Fuzzy Vault）算法，该算法实现了掌纹模糊金库的可撤销性，然而认证性能有待进一步改进。

针对现有掌纹可撤销模板安全性与高效性很难同时实现的问题，本文提出一种基于安全概略（Secure Sketch）的可撤销掌纹模板生成算法。首先对掌纹图像进行Gabor滤波得到不同方向、不同尺度的幅值特征，通过主成分分析（Principal Component Analysis，PCA）算法对其进行降维，然后将加密后的特征向量与BCH码异或融合，得到基于安全概略的可撤销掌纹模板。理论分析和实验结果表明，该算法具有良好的识别性能，能较好地满足可撤销性、多样性和不可逆性，即便在单密钥丢失的情况下，也具有较高的识别率。

2 理论基础

2.1 安全概略

安全概略[17]由一对算法定义，其模型如图1所示，SS为概略算法，REC为恢复算法。w为注册时输入的生物特征，经过SS算法处理生成安全概略s。w′为认证时输入的生物特征，如果w′与w相差很小，也就是生物特征来自同一个用户时，s与w′通过REC算法处理后可以还原出注册时的生物特征信息。

图1 安全概略模型图

定义1 一个(M,m,σ,ε,γ)的安全概略是一对随机过程，其中，ε和γ是小于1的正数，M 为向量空间，这对随机过程具有以下性质：

（1）向量w作为概略算法SS的输入，w∈M，输出为向量s。

（2）w′和s作为恢复算法REC的输入，w′∈M 。如果w′和w差值的汉明距离小于σ，则

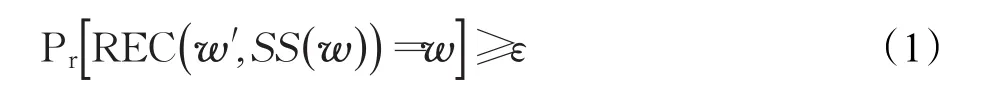
（3）如果w′和w差值的汉明距离大于σ，则

对于任意的M上的分布W，如果W的最小熵大于m，安全概略满足条件：

则称此安全概略是L安全的。本文中所指的熵都是最小熵，而不是香农熵，如果安全概略由多项式时间的算法来实现，称安全概略是有效的。

2.2 Gabor滤波

近年来，Gabor滤波器[18]已经广泛应用于生物特征提取过程中。Gabor滤波器是一组带通滤波器，调节不同的参数可以获得图像空间域、频率域等结构信息。二维Gabor滤波器的定义为：

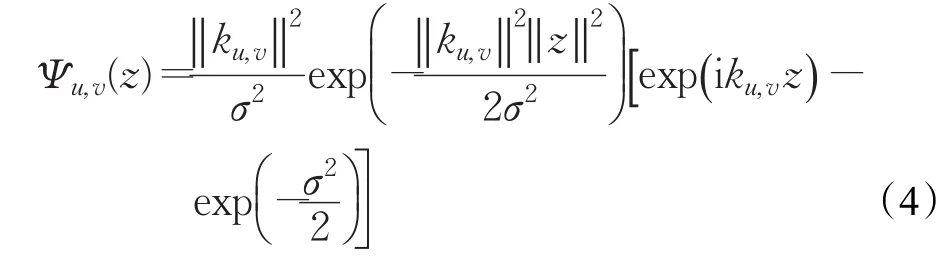
对于图像F(x,y)，其Gabor特征Gu,v(x,y)可通过图像与Gabor滤波器卷积得到：

式中，∗为卷积算子，本文的Gabor特征为图像经Gabor滤波后的幅值部分，如图2所示。

图2 掌纹图像的Gabor纹理特征提取

2.3 PCA算法

在掌纹特征提取过程中，高维的特征数据会导致识别过程复杂、识别时间长等问题，因此，基于PCA[19]算法的掌纹特征提取和识别得到了广泛的运用。源于通信理论中K-L变换的PCA算法，其基本原理是将原有的高维特征数据线性变换，得到一组单位向量正交基，通过正交基的线性组合重构特征空间。经降维后的特征数据不仅保持了原有特征数据的有效信息，而且占用系统资源少，因此通过PCA对掌纹特征数据降维可以提高识别效率。

3 算法原理

针对现有的多数可撤销掌纹模板生成算法在密钥或令牌泄露的情况下，攻击者很容易冒充真实用户进行身份认证的安全问题，本文提出一种可撤销掌纹模板生成算法。首先对掌纹图像进行Gabor滤波得到5个尺度、8个方向的幅值特征，并通过PCA算法对其进行降维；然后将加密后的特征向量与BCH码异或融合，得到基于安全概略的可撤销掌纹模板。与直接提取Gabor特征相比，采用PCA对Gabor滤波后的特征向量进行降维的方法，减小了光照、噪声对识别性能的影响，提高了识别效率。同时引入BCH码，实现了安全概略的构造，提高了算法的安全性，算法流程如图3所示。

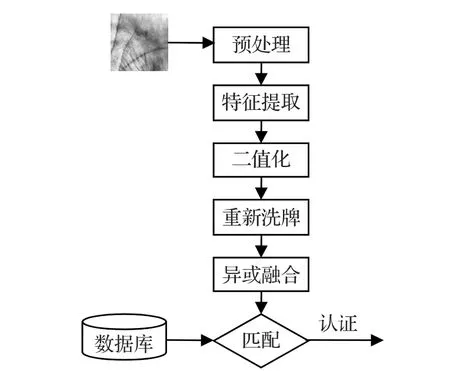
图3 基于安全概略的可撤销模板生成流程

算法的注册阶段步骤如下所示：

步骤1预处理

提取分辨率为128×128的掌纹图像感兴趣区域，并对图像进行中值滤波降噪处理。

步骤2特征提取

（1）Gabor的核函数能够很好地提取目标图像的不同空间位置、频率和方向上的特征，所以在本文算法中生成5个尺度v∈{0,1,2,3,4}和8个方向u∈{0,1,2,3,4,5,6,7}所对应的40个Gabor滤波器组，然后对预处理后的图像进行滤波，每幅掌纹图像分别得到40个幅值图。

（2）经过Gabor滤波后得到的特征含有大量的冗余信息，严重影响识别效率。因此，对每个幅值图分别进行PCA降维生成维数为40的特征向量，每个幅值图特征串联得到掌纹图像的特征向量Γ∈Rm，m=1 600。

（3）由密钥key1生成服从标准正态分布的伪随机数（PN），由PN组成向量，其中

步骤3二值化

为了有效减小用户特定密钥泄露对认证性能的影响，本文采用错位比较的非线性量化方法对特征向量进行不可逆变换，量化后产生维数为n的二值序列。其基本的思想是根据掌纹特征向量X，定义由该特征生成的二值序列Y=[y1,y2,…,yl] 为：

式中，p为步长参数，p∈{1 ,2,…,n-1}，本文实验中p取3。

步骤4重新洗牌

将二值序列Y从左向右每4位分块，共128块，本文中Y的维数为511，所以最后一块的位数为3。生成128位的二进制密钥key2，令key2的顺序与特征块依次对应，特征块与密钥位的1相对应依次左排，与密钥位的0相对应依次右排，洗牌后的二值序列即为掌纹特征模板w。对提取的特征向量进行重新洗牌不仅增强了算法的安全性，而且提高了密钥的多样性与可重用性。

步骤5异或融合

生成一个随机数（RN），对其进行BCH编码得到码字c，将c与w异或融合得到概略，实现安全概略的构造，提高算法的可容错性。

算法的认证阶段步骤如下所示：

步骤1采用与注册阶段相同的方法对掌纹图形进行预处理。

步骤2对预处理后的掌纹图像采用与注册阶段相同的用户密钥key1进行特征提取，其特征为向量X′。

步骤3将特征向量X′不可逆变换得到二值序列Y′。

步骤4对二值序列Y′采用与注册阶段相同的密钥key2进行重新洗牌，得到w′。

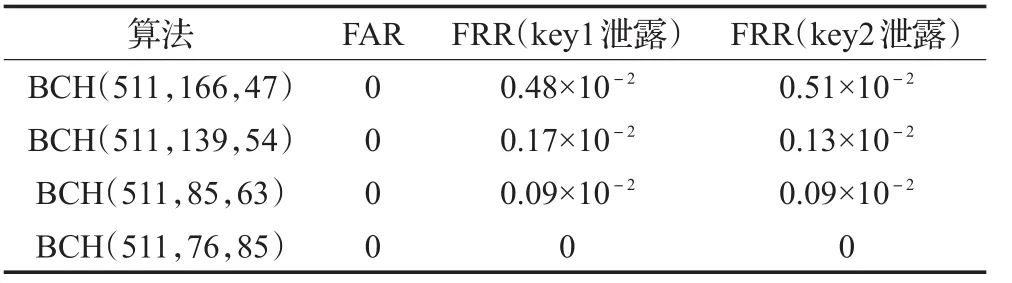
步骤5 计算′，如果c′与c比特位不同的个数t小于BCH纠错码的纠错个数t′，即t

PalmHashing算法是一种重要的可撤销掌纹模板生成算法，通过用户令牌生成的辅助数据与掌纹特征做内积，然后选取一个固定阈值将结果二值化，得到二值序列，通过比较二值序列达到身份认证的目的，在令牌被盗后认证性能会有大幅下降。本文算法采用错位比较的非线性量化方法对掌纹特征向量二值化，有效地消除掌纹特征向量间的大小关系；对二值序列进行分块重新洗牌，避免了令牌被盗认证性大幅下降的情况，同时扩大了密钥空间，提高了算法的可撤销性与不可逆性；引入BCH码，实现了安全概略的构造，提高了算法的可容错性。

4 实验仿真与性能分析

为评价所提出算法的性能，本文在Intel®CoreTMI3-6100，CPU@3.10GHz 4.00GB内存的PC，MatlabR2014a的开发环境下进行实验仿真。采用的数据库为标准掌纹库IITD Palmprint V1.7z[20]。数据库中包含有230个样本，样本分为左右手，每个样本采样6次，而且提供了样本的感兴趣区域标准数据库，如图4所示。

图4 掌纹图像示例

本次实验选取100个样本的前4幅图像作为训练样本。在真匹配实验中，每个样本的第一幅图像作为注册掌纹，第二、三、四幅图像作为查询掌纹，共进行100×3=300次真匹配。在假匹配实验中，每个样本的第一幅图像作为注册掌纹，剩余样本的第一幅图像作为查询掌纹，共进行次假匹配。评价掌纹识别性能的主要参数是误识率（False Accept Rate，FAR）和误拒率（False Reject Rate，FRR）。其中，FAR、FRR值越低可认为算法整体性能越高，所以本文用FAR、FRR来评价算法的有效性。

4.1 认证性能分析

表1给出了密钥泄露时本文算法的FAR、FRR，可以看出不同纠错能力的BCH码，算法的认证性能也不相同。在使用纠错码BCH（511，76，85）情况下，FAR、FRR的值为0，获得了良好的认证性能，即使在单一密钥泄露的情况下仍然具有较好的识别率。因此，本文重点分析使用纠错码BCH（511，76，85）情况下算法的可撤销性、多样性和安全性

表1 本文算法的认证性能

图5给出了在使用纠错码BCH（511，76，85）情况下，本文算法在真假匹配过程中c′与c汉明距离的分布情况。可以看出密钥安全时真匹配的汉明距离分布在0到0.18区间，假匹配的汉明距离分布在0.42到0.58区间，可以全区分不同用户的掌纹，表明本文算法具有较好的识别性能。

图5 本文算法的真假匹配情况

4.2 可撤销性分析

在攻击者获得多个概略s的情况下，攻击者的目标是恢复生物的原始特征。在本文提出的算法中，采取双密钥对掌纹特征进行加密的方式，使不同的用户可以通过不同的密钥生成不同的模板，即便是同一用户生成的模板也是随机的。因此，本文通过定量分析的方法来验证掌纹模板的可撤销性和多样性。具体方案是：选取100个样本的第一幅图像作为实验掌纹，随机生成100对密钥，第一对密钥生成注册模板，其余的密钥生成查询模板，然后将注册模板与查询模板进行匹配（伪假匹配），共进行100×99=9 900次匹配。

图6给出了使用纠错码BCH（511，76，85）情况下，本文算法在真假、伪假匹配过程中与c′与c汉明距离的分布情况。可以看出，真匹配的汉明距离分布在0到0.18区间，假匹配的汉明距离分布在0.42到0.58区间，伪假匹配的汉明距离分布在0.42到0.59区间，说明伪假匹配与假匹配高度相似。所以同一用户可以通过不同的密钥生成不同的模板，本文提出的算法满足可撤销性。

图6 本文算法的真假匹配、伪假匹配分布情况

4.3 多样性分析

生物特征模板的多样性要求不能通过模板间的交叉匹配骗过认证系统。给定两个掌纹图像F1、F2生成的概略分别是s1、s2，攻击者的目的是猜测F1与F2是否来自同一个用户。而s1与s2比特位不同的个数t′的大小取决于F1与F2的相似程度，如果t′小于BCH纠错码的纠错个数t，即t′

4.4 安全性分析

图7（a）和图7（b）分别给出了在使用纠错码BCH（511，76，85）情况下，密钥key1、key2泄漏时 c′与 c汉明距离的分布情况。密钥安全时真匹配的汉明距离分布在0到0.18区间，密钥key1泄漏时假匹配的汉明距离分布在0.41到0.59区间，密钥key2泄漏时假匹配的汉明距离分布在0.42到0.59区间，表明本文算法在单一的密钥泄漏时仍然具有较好的识别性能。在密钥key1、key2全泄漏的情况下，本文算法的识别性能会下降，但是在实际应用过程中可以通过独立生成密钥key1、key2的方式避免密钥全部丢失的情况。例如，其中的一个密钥可以由密码输入的方式来得到，另一密钥则可以从硬件或软件令牌中产生。

本文算法采用错位比较的非线性量化方法对掌纹特征向量进行二值化，有效地消除掌纹特征向量间的大小关系。另外，本次实验生成的掌纹模板长度为511位，当模板遭受到暴力攻击时攻击者需进行2511次尝试，在计算上不可行。因此，系统具有较好的安全性。

5 结束语

图7 密钥泄漏时真假匹配分布情况

时实现的问题，提出一种基于安全概略的可撤销掌纹模板生成算法。在特征加密过程中，采用错位比较的非线性量化方法对掌纹特征向量进行二值化，有效地消除掌纹特征向量间的大小关系。同时引入BCH码，实现了安全概略的构造，提高了算法的可容错性。实验结果表明，该算法具有良好的识别性能，能较好地满足可撤销性、多样性和不可逆性，在单密钥丢失的情况下也保持较高的识别率。需要指出的是单模态生物特征仍然存在一些安全缺陷，因此基于多模态生物特征的模板生成方法，把多种生物特征协同使用以提高特征模板的安全性，是下一步研究的问题。

针对现有掌纹可撤销模板安全性与高效性很难同