基于灰色理论的网络搜索频度数据分析

李 斌，吴庆涛

(1.河南科技大学应用工程学院现代教育技术中心，河南 三门峡 472000; 2.河南科技大学信息工程学院，河南 洛阳 471023)

0 引 言

互联网中包含着海量网络数据，人们的生活方式和行为习惯因为互联网的普及而发生着潜移默化的改变，人们在作各种决策时习惯于通过搜索引擎在互联网上找寻相关信息，并作出各种决策。人们以搜索引擎为桥梁,以搜索关键词为钥匙在互联网中找寻信息,所以搜索关键词在一定程度上代表着人们的关注热点,搜索量则可以代表关注程度。

近年来，对搜索频度的研究一直是各界研究者关注的热点。蒲东齐等[1]利用消费者通过互联网的搜索痕迹与房地产相关的搜索词汇对商品房的价格进行短期预测。高佳玲[2]认为网络搜索关键词数据映射着市场主体的关注点,揭示了市场主体行为趋势,可以为宏观经济问题提供所需要的微观数据。路兴[3]利用与环境相关的网络搜索数据构建指标体系,对我国公众环境关心程度进行评价。孙烨等[4]认为网络搜索引擎是旅游者获取旅游信息的最重要入口,百度指数通过反映关键词被搜索的次数表征旅游者的网络关注度。赵晓龙[5]分析百度指数走势与股票市场指数之间的关系,进而研究互联时代下信息的获取与关注对行为所产生的影响。王若佳[6]通过百度搜索数据分析中文网络关键词和我国流行性疾病监测结果的相关性,拟合并比较各种预测模型,探讨利用网络搜索数据辅助流行病监测的应用可能等。

互联网技术的提高与普及造成了数字信息爆炸，人们对相关关键词的搜索痕迹数量足够大，时效性足够强。结合如上所述的各种搜索频度研究成果，可以利用搜索频度与搜索词汇，对搜索目标热度进行预测，分析热度数据背后的深层次规律。考虑到项目的可行性，本文以“三门峡职业技术学院”为搜索关键词对其周期搜索进行预测和分析。

1 灰色预测理论与构建

1.1 灰色理论研究现状及最新成果

灰色理论属于应用数学，1982年由邓聚龙教授提出，是小样本数据处理工具。灰色预测法[7]是一种对含有不确定因素的系统进行预测的方法。灰色系统是介于白色系统和黑色系统之间的过渡系统。白色系统是指系统内部信息全部已知,即系统的信息是完全充分的。黑色系统是指系统内部信息全部未知,只能通过与外界的联系进行观测研究。灰色系统内的一部分信息是已知的，另一部分信息是未知的，系统内各因素间有不确定的关系。

灰色系统理论着重研究“小样本”、“贫信息”不确定性问题，并依据信息覆盖，通过序列算子的作用探索事物运动的现实规律，其特点是“少数据建模”，着重研究“外延明确，内涵不明确”的对象[8]，预测数据具有原始数据以时间序列形式出现和原始数据可以少到只有4个数据的特点。灰色预测法用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型，生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测未来某一时刻的特征量，或达到某一特征量的时间[9]。

迄今为止，已有多种改进的灰色模型被提出并应用于预测领域。曾冬玲等[10]认为马尔科夫模型结合灰色模型(灰马尔科夫模型)已成功应用于预测领域。李瑶等[11]提出了一种动态优化子集模糊灰马尔科夫预测模型，将计算出的隶属度向量作为马尔科夫转移矩阵向量的权重以修正预测值。李克昭等[12]在传统灰色模型的基础上构造新的背景值，利用正化残差序列修正残差，预测效果良好。张文宇等[13]改进了GM-Markov模型，以西安市年客流量数据为研究对象，建立了以最小预测误差平方和为目标函数的组合预测模型。此外，国外的优化的灰色模型和灰色系统理论的改进也已经取得了很多成果。Wang等[14]提出了一种改进的灰色多变量预测模型，用来预测中国工业能源消费情况。Zhao等[15]研究了混合优化灰色模型，引入滚动机制，以上海市年用电量验证其有效性，用滚动优化的蚁群优化算法结合灰色模型，显著提高了年用电负荷的预测精度。Rezaeianzadeh等[16]结合人工神经网络模型和马尔科夫链模型，提高了短期预测的可能性。这些研究成果说明还需要进一步探究灰色预测模型，根据离群数据来分析其产生机制并进行相应的处理。

1.2 灰色预测模型的构建

灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数，建立起的微分方程形式的模型，这样便于对其变化过程进行研究和描述。灰色预测模型称为GM模型[17]，G为Grey的第一个字母，M为Model的第一个字母。GM(1,1)表示一阶的，一个变量的微分方程型预测模型。GM(1,1)是一阶单序列的线性动态模型，主要用于时间序列预测[18]。

GM(1，1)的建模步骤如下：

1)对非负的原始时间序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n))做一阶累加得到生成数据序列X(1)=(x(1)(1),x(1)(2),…,x(1)(n))，其中x(1)(1)=x(0)(1), x(1)(k)=x(1)(k-1)+x(0)(k), k=2,3,…,n。

2)令Z(1)为X(1)均值系列：Z(1)=(z(1)(1),z(1)(2),…,z(1)(n))，其中z(1)(1)=0.5x(1)(1), z(1)(k)=0.5((x(1)(k)+x(1)(k-1)), k=2,3,…,n，则GM(1，1)的灰微分方程模型为：

x(0)(k)+az(1)(k)=b

其中a是常数，称为发展灰数；b称为内生控制灰数，是对系统的常定输入。对应的白化方程为：

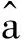
其中：

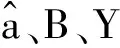
其中t=1,2,…,n，用后减运算还原，即可得到原始序列X(0)的预测值[19]：

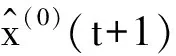
后验差检验分别计算：

X(0)的均值：

X(0)的方差：

残差的均值：

残差的方差：

后验差比值：

小误差概率：

最后重点判决后验差比值C和小误差概率P，小误差概率P≥0.9，预测精度在C>0.95或C<0.35时为好，在C>0.80或C<0.45时为合格。符合这些数值的表面原始序列预测方程可用，然后将不同时间区间数目代入即可预测出相应时间段的预测值[20-21]。

2 灰色预测模型验证与数据分析

2.1 搜索热词可视化

互联网世界资讯信息种类繁多，网络渠道多样化。经调查发现某些内容的网络搜索数量显著，分析搜集某年的相关网络内容，其数据不多。但若将时间间隔放大，或是以存在明显变化者作为预测内容，则能够搜集到较完整数据。大数据是统计与计算机相结合发展的过程，即通过对经济社会活动与经济社会关系的定量、定性的观测与实验等过程，引入科学的技术和方法，达到对各种规律的有效把控、利用和管理的目的[22]。社交网络交互数据及移动互联网数据等方式获得的各种类型的结构化、半结构化及非结构化的海量数据，是大数据知识服务模型的根本[23]。

在获得原始数据后，利用灰色系统理论的灰预测作为预测工具，验证预测模型的误差率是否可用，再利用Matlab工具批量进行计算，得到预测值，然后与历史数据进行统一分析对比，以达到数据分析的目的[24]。本文以“三门峡职业技术学院”为百度搜索关键词，探索此类大数据的共性分析。

图1是2011年初至2017年底期间“三门峡职业技术学院”一词百度搜索周指数变化曲线。分析词汇热度变化趋势图发现：7年多的时间内，“三门峡职业技术学院”一词的热度变化趋势呈看似杂乱无章的波浪起伏状态。抛弃个别周可能因为突发热点引起的周搜索指数偏高外，7年中周平均搜索指数大致为800～1000。

图1 “三门峡职业技术学院”一词百度搜索周指数变化

2.2 数据搜集和灰色模型预测验证

网络爬虫是一种较为常见的方式，爬虫通过追踪网上的超链接可以获取互联网中对应的资源[25]。利用网络爬虫软件从百度指数曲线上抓取2012-2017年“三门峡职业技术学院”一词的百度周搜索指数，计52周×6年共312个数，如表1所示。按照灰色预测模型，按年度分析数据的内在变化趋势，预测2017年的周值，并与实际周值进行精度检测。若符合精度误差范围则证明预测模型的时间响应方程可用，并预测出2018年及2019年的热词周搜索指数。

表1 每周搜索次数(2012年1月至2017年12月)

周1234567891011121314151617181920212223242526年度201220132014201520162017344651683700965994366430639115714991792413496524744916144641650755872513961456185352418595607711220244384393408679224278282367506773239306343457996155634740343870111631375561836914112515621618696760788112213501482774856875917954133174485389511071107118746370074675696411273944436948358479694335368088559741147487524646769771127337645058967579085441647857881183611644504956778128779753934577257738109853974246777357408764125466547147369065215426206518511181554680893107511811440344651683700965994周2728293031323334353637383940414243444546474849505152年度2012201320142015201620176786861046112812611406863110215911744214125569271145115115791625179244773875381584113784124285466266727414404705776016208625376717528649891390589102611031202167420067331037106011591197130672399099910691089132989010761201124614871691750786961114112411328480625752753864111950952363071282486031438545847448750029229749451865670943143745948064967739039943344561892036537940841855372835136469297510661139406419471536574648373419445451512561347363397405497553305365377378597629332335389393601753339371372411606746

以每年的第1周为例，从2012年到2016年的原始序列(考虑矩阵的计算方便左移3位小数点，计算完毕后右移3位小数点即可)为X(0)=(0.344, 0.651, 0.683, 0.700, 0.965),由原始序列计算一次累加序列得X(1)=(0.344, 0.995, 1.678, 2.378, 3.343)。

如前述，建立矩阵：

计算(BTB)-1,并求出a、b：

将a和b代入时间响应方程，由于X(1)(1)=0.344，故GM(1,1)预测模型的时间响应方程为：

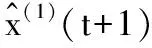
=4.14076e0.1358t-3.79676

表2 第1周搜索次数计算列表(2012-2017年)

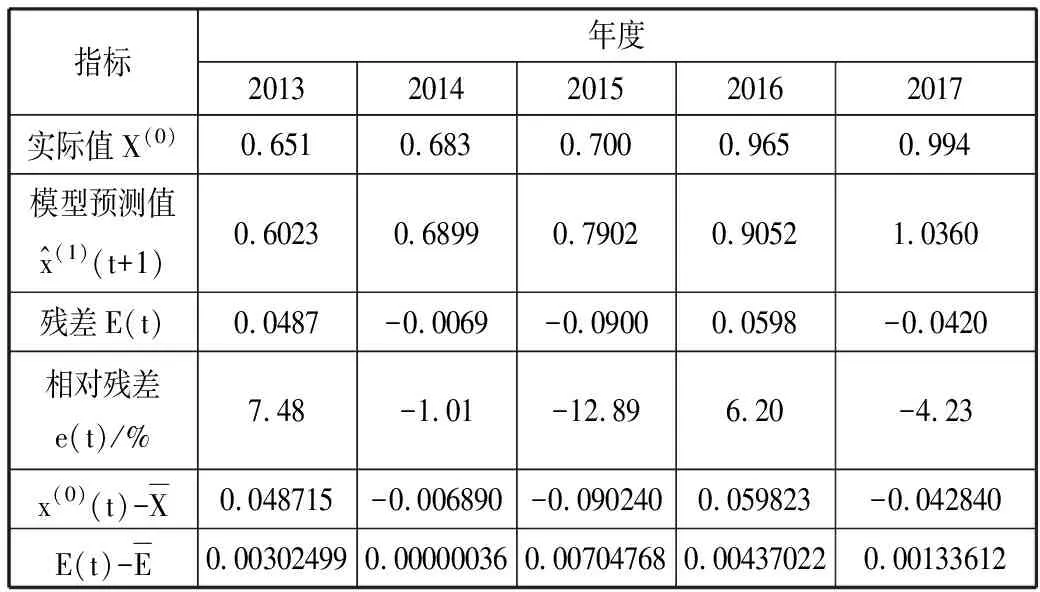
指标年度20132014201520162017实际值X(0)0.6510.6830.7000.9650.994模型预测值^x(1)(t+1)0.60230.68990.79020.90521.0360残差E(t)0.0487-0.0069-0.09000.0598-0.0420相对残差e(t)/%7.48-1.01-12.896.20-4.23x(0)(t)-X0.048715-0.006890-0.0902400.059823-0.042840E(t)-E0.003024990.000000360.007047680.004370220.00133612

X(0)的均值：

X(0)的方差：

残差的均值：

残差的方差：

后验差比值：

小误差概率：

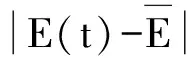
根据P≥0.95, C=0.422<0.45，表示预测等级合格，由此可知下列预测方程可用。

进行外推预测，依次令t=6, 7，代入第1周灰色模型的时间确认方程得：

后减运算得2018年度、2019年度第1周的热词搜索次数预测数为：

截止本文投稿时，百度指数曲线上2018年度第1周“三门峡职业技术学院”关键词的搜索次数实际值为1023，与本模型预测值偏移量为125，误差率为13%，基本符合预测期望值，进一步说明了本模型预测方程可用。

依此类推，可以利用GM(1,1)预测模型预测在一年内的热词搜索得到2018、2019年度对应时间周次“三门峡职业技术学院”的热词搜索次数。需要指出的是，每年内各个时间周存在一定的突发因素会导致搜索次数存在一定的误差，这也是上述预测等级仅为合格而不是较好的主要原因，但总体数据误差应在可以接受的范围内。鉴于计算繁琐，可以利用Matlab编程工具实现，具体程序如图2所示。

图2 Matlab程序源代码

为进一步验证此GM(1,1)模型的可用度，因为可以明显看出每年相同周数据基本呈线性增长，所以仍以第1周数据构建一元回归模型[26]预测以与GM(1,1)模型进行对比验证。

取年度时间数据为自变量，周搜索次数为因变量，运用SPSS软件来实现预测。预测过程如图3所示。

模型汇总

a.预测变量：(常量),X。

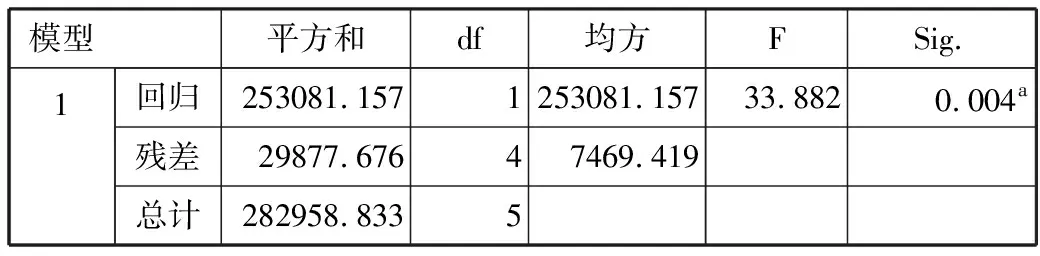
Anovab

a.预测变量：(常量),X。b.因变量：Y

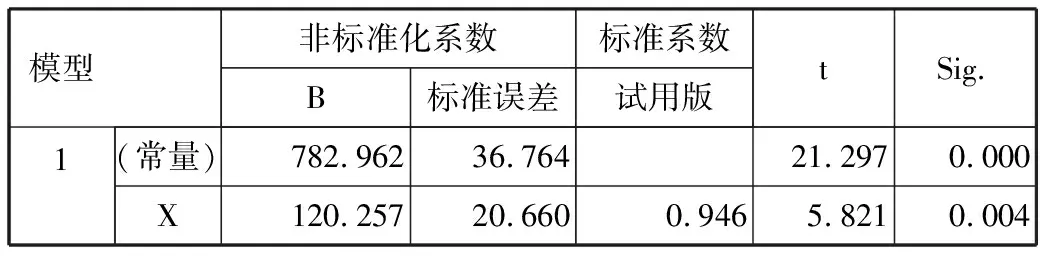
系数a

a.因变量：Y

图3 SPSS一元回归分析结果图

从图3中可以知道模型的复相关系数(R)为0.946，所以回归方程的拟合度达到要求。可知回归方程的统计量F值为33.882, P值为0.004，方程很显著。可知回归方程的常数项为782.962，回归系数为120.257，所以第1周的回归方程为：

Y=782.962+120.257x

根据此方程可得2018年第1周的预测值为1143.7。以此类推，可以预测出2018年每周的预测值，并生成图表与GM(1,1)预测值对比如图4所示。从图中对比折线图可以明显看出，2种预测模型的预测结果高度重合，这说明GM(1,1)模型预测值的科学性和准确性更具合理性。

大数据的核心和目标就是预测，所以需要根据监测数据开展热度预测[27]，根据预测出来的数据和历史数据对比后进行深度分析。出于篇幅原因，根据每周的搜索指数预测模型推导出来的2018年和2019年关键词搜索预测次数就不再以数据方式列表，而是和2012年以来每周周搜索指数生成直观的图表，如图5所示。

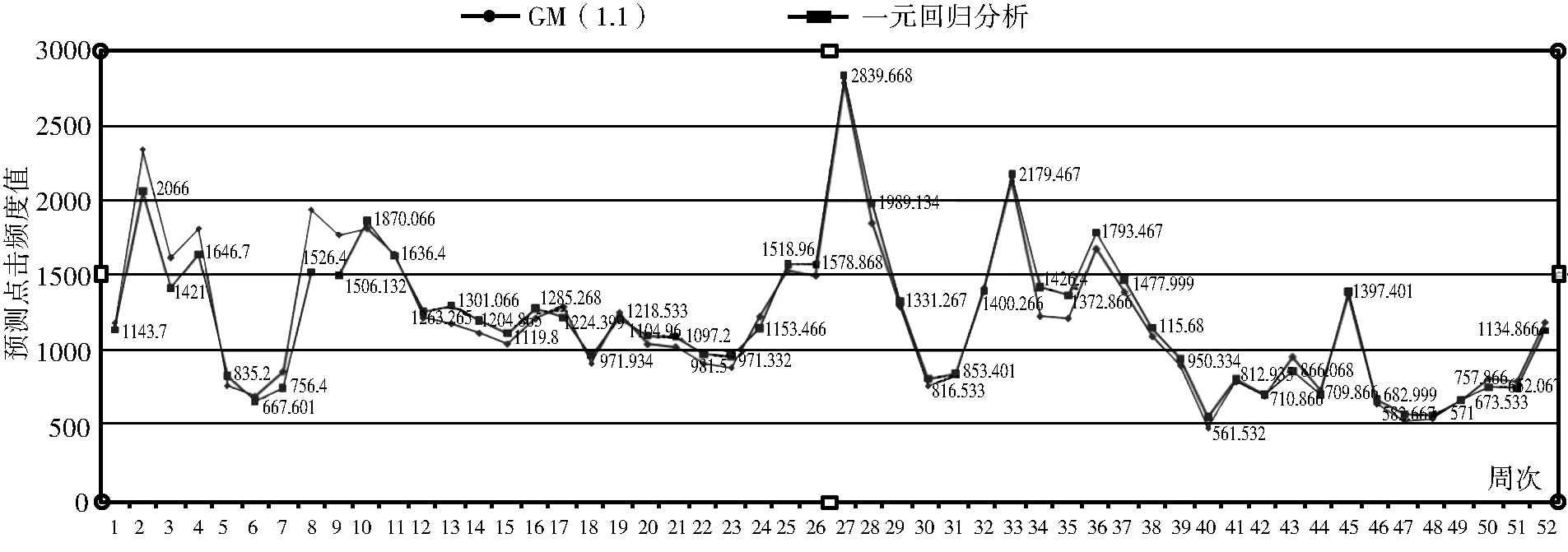
图4 2种预测模型2018年预测结果对比图

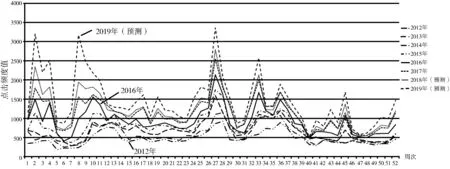
图5 百度搜索关键词“三门峡职业技术学院”周指数按年份统计对比图

3 结果分析

3.1 可信度大数据分析

大数据分析是将描述性的、诊断性的、预测性的和规定性的模型用于数据,来回答特定的问题或发现新的见解的过程[28]。大数据分析通常仅指使用预测分析、用户行为分析或某些其他高级数据的分析方法，这些方法从数据中提取价值，很少涉及特定大小的数据集[29]。虽然现在互联网关注某关键词渠道来源多样，比如知乎、有道、论坛以及各类手机端APP等，但百度周搜索指数作为观察指标目前还是具有一定的权威性，因此本文的统计数据具有一定的可信度和观察指标代表性。

3.2 指数变化特征分析

由图5可以直观看出，从2012年开始到按照预测模型预测出来的2018年、2019年“三门峡职业技术学院”作为百度搜索关键词有着显著的时间特征。1)总搜索次数每年呈递增趋势，这与该校近年持续良好的发展势头正相关，反映了社会各界对该学校办学力量的关注度持续上升。2)从图5可以清晰地看出，百度关键词周搜索次数在一年内的各周峰谷值有着明显的起伏规律，比如每年的第3～4、8～10、26～29、33～34、36～37、45、52周搜索次数急剧上升，结合学校实际情况，可以推测出第3～4、36～37周应为师生搜索校教务系统查分居多，第8～10周应为学校单招前各地学生查询学校情况和报名情况为主，第26～29周以及第33～34周的搜索次数飙升应为高考填报志愿及批次录取时的查询较多。但第45周和第52周处于国庆假期和元旦假期前，搜索次数上升主要影响因素为何，仍需深入分析其原因。

4 结束语

本文虽是以“三门峡职业技术学院”为搜索关键词，但预测结果及数据直观图同样对其他各高校有可参考性。按照灰色预测模型得到的后2年预测值，结合直观的图表分析，参考从大数据中挖掘的信息，作为校方应该正视的数据信息，可使即将到来的新学年有的放矢：1)要做到继续提升自身内涵及扩大宣传，持续提升学校总体影响力。2)要注重挖掘搜索低谷时间周内的潜在信息，比如在假期中多引导学生利用顶岗实习系统和学校沟通等，引发热点、制造沸点、扩大亮点。3)要将重点时间放在上述峰值周，峰值周正是影响高校招生录取工作的关键阶段，要广泛利用其他各种媒介，以正能量信息全面覆盖宣传面，以个体的被动搜索引发蝴蝶效应，促进总体的主动搜索，带动媒体的全面关注，从而为数据增加更多的新信息，实现数据产生价值的良性循环。

考虑到其他诸如每年寒暑假时间段不同、突发热度事件等外在因素对预测值的的交叉影响，GM(1,1)预测模型亦有其不足之处，难免会出现偏差，如何改进此模型以达到更高的预测精度，是后续研究仍需解决的问题。