滚轮滑轨磨损可靠性研究
孙 文 ,任 涛,康晓清,王三民
(1.西安石油大学 机械工程学院,陕西 西安 710065;2.西北工业大学 机电学院,陕西 西安 710072)
1 引言
滚轮滑轨的滚动接触在工程领域中普遍存在,例如铁路机车车辆轮轨、飞机襟翼运动机构、摆杆式抽油机中滚轮摆杆机构等。滚轮或滑轨磨损失效会导致滚轮滑轨强度减小、工作能力丧失及滚轮滑轨运动机构卡阻等,因此,滚轮滑轨磨损可靠性分析显得尤为重要。在基础理论及工程应用方面,国内外很多学者开展了滚轮滑轨磨损的相关研究[1-5]。
对于滚动接触的滚轮滑轨,在不同的工程领域中,滚轮和滑轨有不同的基本形状,目前针对圆柱形滚轮和圆柱形滑轨的磨损可靠性分析比较少见。基于Archard模型,利用切向滑动方程计算滑动距离,给出了接触应力的计算模型,确定了磨损系数和允许磨损量的选择依据,提出了滚轮滑轨磨损可靠性分析方法,并进行了实例分析。
2 磨损计算基本数学模型
不同领域材料磨损计算模型有多种[6],其中Archard模型在摩擦磨损领域应用最为广泛。用磨损深度表示的Archard磨损量计算公式为[3-4,6-7]。

式中:Wd—磨损深度(m);Kw—磨损系数(无量纲);p—接触应力(Pa);L—滑动距离(m),即磨损距离;H—材料硬度(Pa),材料屈服强度σs较材料硬度H更易获得,一般情况下可取H≈σs[4,7]。
2.1 接触应力

图1 滚轮滑轨接触受力简化示意图Fig.1 The Diagram of Roller and Slide Rail’s Contact Model
对于滚轮和滑轨的基本形状皆为圆柱形而言,滚轮与滑轨接触可以简化成圆柱体在无限半空间弹性体表面上滚动,二维滚动接触,如图1所示。
接触表面上所承受的应力分布由赫兹理论给出,对于二维情况来说,接触应力分布(一般也称为压力分布)呈半椭圆形,即[5]:

式中:px—沿x轴分布的接触应力(Pa);p0—最大接触应力(Pa),即沿x轴分布的最大压应力;a—接触面宽度的一半(m);F—作用于接触面上的法向总载荷(N);B—初始接触线长度(m);ρ1—滚轮滚动半径(m);μ1、μ2—滚轮材料和滑轨材料的泊松比(无量纲);E1、E2—滚轮材料和滑轨材料的弹性模量(Pa)。
初始接触线处的压应力p0最大,实际计算时一般以此压应力代表滚轮滑轨接触受力后的接触应力。基于Archard模型进行磨损量分析计算时,可以用最大接触应力p0表示式(1)中的接触应力p。
2.2 滑动距离
2.2.1 切向滑动方程
滚轮沿滑轨滚动时,接触面总的滑动量包括刚性滑动量和弹性滑动量。切向滑动方程可以用来分析接触面总的滑动量。切向滑动方程可用接触面的局部坐标、弹性位移、刚性蠕滑率来表示。接触面的局部坐标系由图1确定,纵向为滚动方向,即x轴方向,横向根据x轴和z轴,按照右手定律确定,即y轴方向。对于稳态滚动接触情况,接触面上不同点(x,y)的切向滑动方程为[3,5]:

式中:ω1,ω2—纵向总蠕滑率和横向总蠕滑率(无量纲);ε1—纵向平动刚性蠕滑率(无量纲);ε2—横向平动刚性蠕滑率(无量纲);ε3—自旋蠕滑率(m-1);u1,u2—沿纵向和横向的弹性位移(m)。
对于圆柱滚轮而言,忽略设备装配及零件制造产生的尺寸影响,认为所有的滚轮同步运动,则不考虑由纵向平动刚性蠕滑率ε1及横向平动刚性蠕滑率ε2引起的刚性滑动。对于二维滚动接触问题,自旋蠕滑率ε3=0,横向总蠕滑率ω2=0,则式(3)简化为:

由纵向总蠕滑率ω1可得滚轮滑轨相对滑动速度,即[5]:

式中:vs—滚轮滑轨相对滑动速度(m/s);v0—滚轮滚动速度,即滚轮沿滑轨前进的名义速度(m/s)。
2.2.2 应变梯度
滚轮与滑轨接触可以简化成圆柱在无限半空间弹性体表面上滚动。两个弹性体接触表面是一个矩形。接触表面区域分成两部分,沿着前进方向的阴影部分为粘着区,在粘着区不存在滑动,后面部分为滑动区,滑动区存在着相互压紧的弹性体材料的微量弹性变形[5],如图2所示。随着切向力的增大,接触面内的滑动区域逐渐增大,直至整个接触面区域为滑动区。
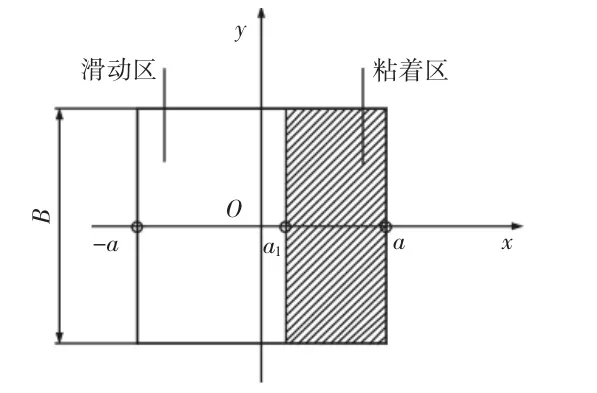
图2 接触面区域的滑动区与粘着区Fig.2 Slip Area and Stick Area
对于二维滚动接触问题,根据文献[5,8],可以确定滑动区域内圆柱体的滑动切向力、切向弹性位移及应变梯度为:

式中:pr1—圆柱体的滑动切向力(Pa);ur1—圆柱体的切向弹性位移(m),其中当x≥0时取正号,当x<0时取负号—圆柱体切向弹性位移的应变梯度;f—动摩擦系数;δ*r1—圆柱体上原点O相对无穷远处的切向弹性位移量(m),且δ*r1>0。滑轨与滚轮作用力相反,同理可得滑动区域内滑轨的滑动切向力、切向弹性位移及应变梯度为[5,8]。

式中:ps1—滑轨的滑动切向力(Pa);us1—滑轨的切向弹性位移(m)其中当x≥0时取正号,当x<0时取负号—滑轨切向弹性位移的应变梯度—滑轨上原点O相对无穷远处的切向弹性位移量(m)则滑动区域内切向弹性位移差的应变梯度为:

2.2.3 滑动距离
滚轮沿滑轨滚动时,接触面滑动区域内一个微元dx滑动距离Ldx为蠕滑率与微元的乘积,即Ldx=ω1×dx,则整个接触面滑动区域滑动距离可以通过积分计算,即:
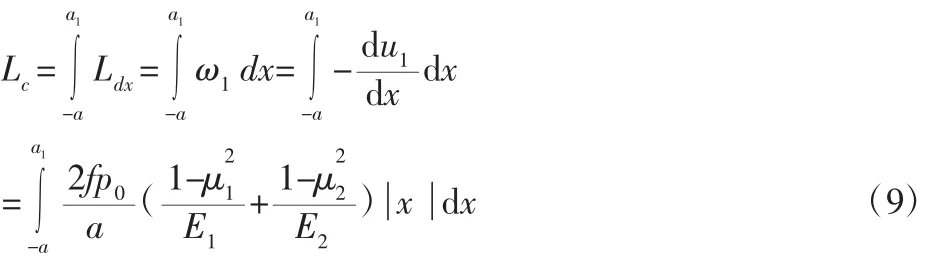
式中:Lc—整个接触面滑动区域滑动距离(m)。
实际上,接触面区域的粘着区必须存在,如果粘着区消失,则滚轮滚动变成了宏观上的纯滑动或者空转。为了便于工程应用的计算,可以假设接触面区域内滑动区接近于全部接触面区域面积,即a1=a,这样在滚轮滑轨磨损计算时偏于安全。
根据Lc可以得到总的滑动距离L,对于不同设备,滚轮滑轨总的滑动距离L计算公式会有所不同,要根据情况具体分析。
2.3 磨损系数
磨损系数包含着除了接触应力p(或者载荷F)、滑动距离L、材料表面硬度H之外的所有影响磨损的因素,其值能否合理地给出,是计算实际磨损量的关键。目前,确定磨损系数常采用的方法有经验法、试验法和查磨损因数表法。
为了进行铁路机车车辆轮轨摩擦磨损分析,Jendel给出了磨损系数随接触应力p和轮轨相对滑动速度VS的变化情况[3,9],如图3所示。图3所确定的磨损系数在轮轨摩擦磨损领域得到了广泛的应用。因此,基于Archard模型的滚轮滑轨磨损分析,可以依据接触应力p和轮轨相对滑动速度vs通过图3选取磨损系数。磨损系数的均值取不同区域里面的中间数值,磨损系数的标准差按照“3σ原则”选取。

图3 磨损系数Fig.3 Wear Coefficient
3 磨损可靠性分析
3.1 磨损可靠度数学模型
在给定的工作时间内,摩擦副的表面磨损总量小于等于其允许磨损量(最大磨损量)的概率,称之为磨损可靠度(耐磨可靠度),即:
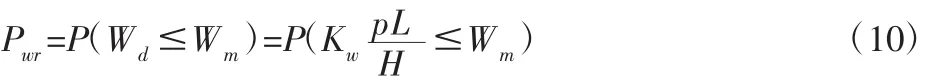
式中:Pwr—磨损可靠度;Wd—磨损深度(m);Wm—允许磨损量(m),即最大磨损量。
3.2 允许磨损量
对于滚轮滑轨磨损可靠性分析,当实际磨损量大于允许磨损量时,则运动机构失效。允许磨损量可以通过使用经验、试验结果或者计算分析来确定。
不同的运动机构允许磨损量是不同的。应该综合考虑载荷、机构运动精度、材料、加工工艺等因素进行确定。例如,新型摆动导杆式抽油机属于石油矿场机械,机构运动精度要求低,工作载荷具有明确的周期性,滚轮属于易磨损零件。如果滚轮零件采用表面淬火或者渗碳等热处理工艺,则可以根据滚轮零件的淬透层深度或者渗碳层深度确定允许磨损量。
3.3 磨损可靠性分析方法
蒙特卡洛中心正态重要抽样法(简称MCCNIS法)[10],将重要抽样密度函数的中心放在极限状态方程的设计点,使得样本落在失效域的概率在50%左右,从而提高了计算效率,是比较常用的重要方法。
假设Wm、p、L、Kw和H服从正态分布,为了便于描述,随机变量Wm、p、L、Kw和H用X(ii=1,2,…,5)表示,整体用向量X表示,即X=(X1,X2,X3,X4,X5);样本值用x(ii=1,2,…,5)表示,整体用向量 x 表示,即一次抽样的样本值为 x=(x1,x2,x3,x4,x5),如果进行N次抽样,样本值整体用向量j=1,2,…,N)表示,即xj=(x1j,x2j,x3j,x4j,x5j);功能函数(极限状态函数)用 g(X)表示;联合概率密度函数用表示;联合重要抽样概率密度函数用h表示;利用MCCNIS法进行磨损可靠性分析的流程图,如图4所示。

图4 MCCNIS法计算磨损可靠性流程图Fig.4 Flow Chart of MCCNIS for Calculating Wear Reliability

表1 随机变量分布参数Tab.1 Distributed Parameters of Random Variables
4 实例分析
4.1 随机变量分布参数
某新型摆动导杆式抽油机中滚轮滑轨运动机构采用圆柱滚轮与标准钢轨(GB2585-2007)。已知滚轮和滑轨的弹性模量E1=E2=206×109Pa;滚轮和滑轨的泊松比为 μ1=μ2=0.3;动摩擦系数 f=0.3;滚轮滚动半径ρ1=60mm;初始接触线长度B=40mm;冲次N=6min-1,冲程 S=2.5m。
根据新型摆动导杆式抽油机的理论工况和滚轮滑轨受力分析,可得滚轮接触应力p的分布参数;允许磨损量根据滚轮零件的淬透层深度确定,变异系数可取经验值;滚轮磨损距离(滑动距离)计算,如表1所示。其中,Lc由式(9)确定,Ls为一个冲次的滚轮滑动距离,L为工作t天的滚轮滑动距离,且可由L的计算公式可知,如表1所示。如果不考虑冲次、冲程、滚轮半径的变异系数,则可以用接触应力p0的变异系数(即接触应力p的变异系数)来表示磨损距离的变异系数;磨损系数由图3选取,不同区域里面的磨损系数可以取其中间数值代替磨损系数均值,磨损系数的标准差按照“3σ 原则”选取;材料硬度可取H≈3σs[4,7],材料硬度变异系数可取经验值。
新型摆动导杆式抽油机滚轮滑轨磨损分析计算采用Archard模型,各随机变量可视为正态分布,其具体分布参数,如表1所示。
4.2 结果计算及分析
利用MCCNIS法进行滚轮磨损可靠性分析,滚轮磨损可靠度与工作时间的关系曲线,如图5所示。给定可靠度Pwr=0.99、给定可靠度Pwr=0.95和给定可靠度Pwr=0.90的计算结果,如表2所示。

图5 滚轮磨损可靠度与工作时间的关系曲线Fig.5 Curve of Roller’s Wear Reliability and Time

表2 滚轮磨损可靠性计算结果Tab.2 Calculation Results of Roller’s Wear Reliability
由图5和表2可得以下结论:
(1)由图5可知,在工作时间小于650天左右以前,新型摆动导杆式抽油机滚轮磨损可靠度曲线变化很小,几乎为一直线;工作时间超过650左右时,新型摆动导杆式抽油机滚轮磨损可靠度下降逐渐明显。
(2)由表2可知,当给定可靠度Pwr=0.99时,滚轮工作时间为570天;当给定可靠度Pwr=0.95时,滚轮工作时间为676天;当给定可靠度Pwr=0.90时,滚轮工作时间为743天。
(3)根据工程上不同的可靠性要求,计算结果可为工程设计人员确定滚轮滑轨维护周期提供依据。由上述(1)和(2)分析可知,在理论工况下,新型摆动导杆式抽油机滚轮维护周期在(650~700)天左右时比较合理。
5 结论
滚轮滑轨的滚动接触在工程领域中普遍存在,目前针对滚轮和滑轨基本形状皆为圆柱形的磨损可靠性分析比较少见。基于Archard模型,给出了接触应力的计算模型,利用切向滑动方程计算滑动距离,确定了磨损系数和允许磨损量的选择依据,提出了滚轮滑轨磨损可靠性分析方法。根据工程上不同的可靠性要求,基于提出的方法,计算结果可为工程设计人员确定滚轮滑轨维护周期提供依据。

