人体下肢外骨骼康复机器人的动力学分析与研究

夏 田，桓 茜，陈 宇，徐建林

（陕西科技大学 机电工程学院，陕西 西安 710021）

1 引言

外骨骼机器人是一种将人体和仿人型机械结构连接于一体的并联机构装置，而这种并联机构又有其独特性，人体在这个装置中基本上是受力者，不需要为外骨骼的运动施力，即外骨骼需要实现在不干扰人体运动的前提下实现助力效果，所以外骨骼机器人的动力学研究是外骨骼技术研究的基本问题之一[1-3]。

下肢外骨骼动力学分析的目的是为了求解各关节在运动状态下所受的力和力矩，为此在分析过程中，将其简化为七杆机构，包含六个关节（两个髋关节、两个膝关节和两个踝关节），然后运用当前常用的划分行走模式方法将动力学研究建立在不同的行走模式下进行动力学建模分析，最后在ADAMS环境下进行人机耦合的动力学仿真，求解关节力矩与运动周期的曲线关系。

2 下肢外骨骼结构原理

以身高为175mm的人体为例，根据《GB/T 1000-1988中国成年人人体尺寸》，将下肢外骨骼康复机器人的各部位尺寸设计为[7]：髋部长度l1=334 mm，大腿连杆长度l2=428 mm，小腿连杆长度l3=430 mm，脚部尺寸l4=68mm。人体下肢各关节的自由度和活动度，如表1所示。

为一种基于液压驱动型的人体下肢外骨骼康复机器人结构示意图，如图1所示。其各连接部件采用铝合金材料；背部、腰部和腿部的束紧带为柔性构件，材料为尼龙。

表1 下肢各关节自由度和活动度Tab.1 Degrees of Freedom and Rang of Motion

下肢外骨骼的结构主要包括背部穿戴装置、大腿部驱动机构和踝部驱动机构。各个构件的不同连接和配合方式，可以实现髋关节的3个自由度，膝关节的1个自由度，踝关节的3个自由度，起着连接和驱动支撑部分运动的作用。

此外，分别在髋关节和踝关节处设置一组液压驱动系统，用来带动大腿摆动和脚部支撑，大腿和小腿之间没有设置液压系统是因为小腿在大腿摆动时可以凭借惯性实现随动的摆动，这样可以减轻装置的重量。

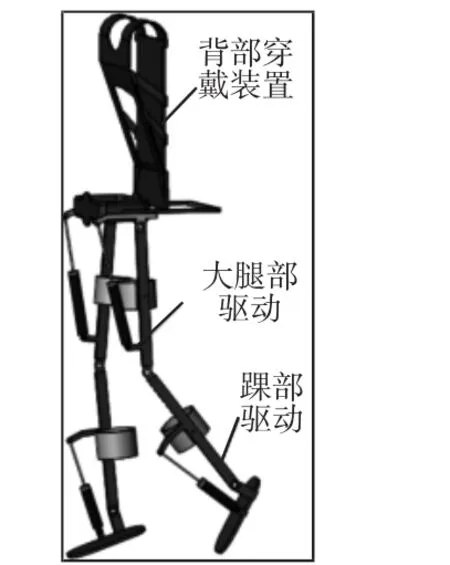
图1 外骨骼机器人示意结构Fig.1 Schematic Structure of Exoskeleton Robot

3 动力学方法的确立

多刚体系统动力学分析常用的方法是拉格朗日方法和牛顿-欧拉方法。拉格朗日方法是根据全部杆件的动能和势能求出拉格朗日函数，导出机械运动方程，求出各关节的力矩，该方法不用考虑内部不同杆件的作用力，在一定程度上简化了力矩的求解，为动力学研究提供了便利[4]。但在外骨骼机器人的动力学分析中需要了解每一杆件的具体受力情况，为机构设计和材料选择提供理论指导，从而设计出与人体高度耦合的外骨骼装置。

牛顿-欧拉方法满足了局部受力分析的需要，它将杆件的相互约束力及相对运动作为向量进行处理，根据力与力矩的平衡来推导运动方程，该方法计算简单、高效，计算量与机器人的自由度成正比，关键的是可以显示任何杆件的空间受力情况[5]，其受力分析，如图2所示。

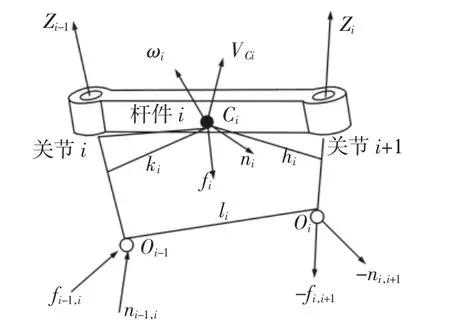
图2 单杆件受力图及物理参数Fig.2 Force and Physical Parameters of Single Lever

图中：Oi-1，Oi—杆件 i两端的坐标系原点；Ci—杆件的质心；Li—杆件 i两端坐标系原点的距离；Ki、hi—质心 Ci到 Oi-1、Oi的距离；fi-1，i、-fi，i+1—杆件 i-1 作用在杆件 i上的力和反作用力；ni-1，i、-ni，i+1—杆件 i-1作用在杆件i上的力矩和反作用力矩；fi—作用在杆件i上的外力化简到质心Ci处的合力；ni—作用在杆件i上的外力矩化简到质心Ci处的合力矩；Vci—杆件质心的平移速度；ωi—杆件i质心的转动角速度。

已知杆件的质量为mi，质心在Ci点，如图2所示。质心处的加速度为aci，绕质心的角速度和角加速度分别为ωi和εi，根据牛顿方程可得作用在杆件质心Ci处的力为：

根据欧拉方程作用在杆件i上的力矩为：

式中：ICi—杆件Li相对于其质心Ci的惯性张量，即

对构件i进行独立受力分析，由合力和合力矩定理得：

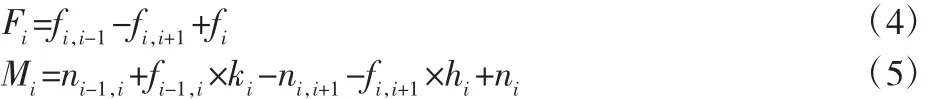
4 下肢外骨骼动力学建模

人体外骨骼的运动遍布人体的三个基本平面（矢状面、额状面和水平面），额状面和水平面内的运动是局部细微的，运动不太明显，其运动主要集中在矢状面内，故主要以外骨骼机器人在矢状面内的运动为研究对象[6]。

在一个步态周期内，人体下肢双腿与地面之间存在单脚支撑和双脚支撑两种行走模式，在进行动力学分析时，可以将下肢外骨骼各关节的力矩变化建立在步态行走的不同模式上，分别运用牛顿-欧拉方法建立相应的动力学数学模型，

4.1 单脚支撑行走模式

单脚支撑行走模式下，外骨骼系统从支撑脚与地面接触的位置到摆动腿自由运动末端可以看作是一个多刚体的开环链式结构。下肢外骨骼系统单脚支撑行走简化模型，如图3所示。

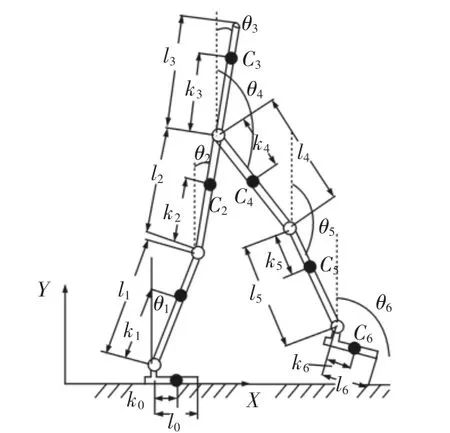
图3 单脚支撑行走模式Fig.3 Single Foot Support Walking Pattern

图中：（xh，yh）—绝对坐标系OXY下支撑脚踝关节的绝对坐标；θi—杆件i与竖直方向的夹角（属于绝对角度，以逆时针方向为正）；Ci—各杆件质心；mi—各杆件质量；li—杆件 i的长度；ki—杆件 i的质心到关节的距离，其中 i=0，1，…，6。

各个杆件质心Ci的坐标可表示为：

杆件质心的加速度aci为：

式中：qi—杆件参数，当 i=0，1，2，4，5，6 时，qi=1；当 i=3 时，qi=0；cθ=cosθ，sθ=sinθ。

下肢外骨骼单脚支撑行走模式下各杆件受力模型，如图4所示。其符号说明与图3一致。对外骨骼进行动力学分析的目的是求解出各个关节的输出力矩，即 n0，1，n1，2，n2，3，n3，4，n4，5，n5，6，为机器人驱动器的选择提供参数依据。

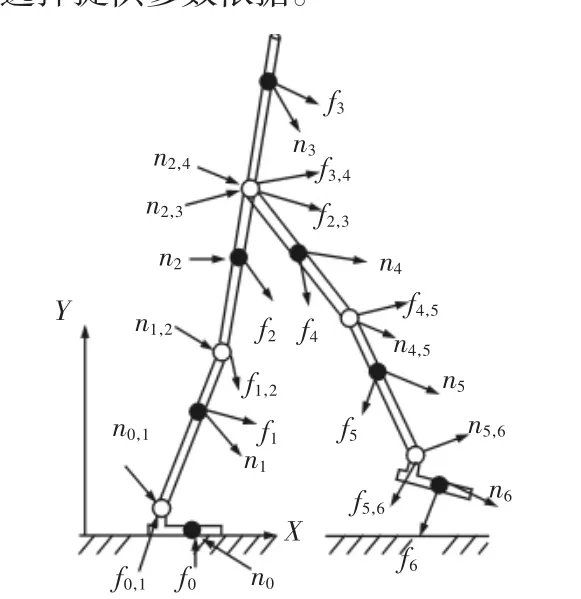
图4 单脚支撑动力学模型Fig.4 Dynamics Model of Single Foot Support

外骨骼的动力学模型的建立是从支撑脚到摆动脚，求解关节的扭矩则采用逆解法，即先求末端杆件的关节驱动扭矩，再逆向顺次求出各个关节的扭矩，具体求解过程如下：

结合式（1）和式（4）、式（2）和式（5）建立杆件6的牛顿-欧拉方程为：

将运动学分析中求解的各关节的角速度、角加速度时间曲线，带入上式求出 f5，6，n5，6。同理，可以依次求出 f4，5、n4，5、f3，4、n3，4、f2，3、n2，3、f1，2、n1，2、f0，1、n0，1。

4.2 双脚支撑行走模式

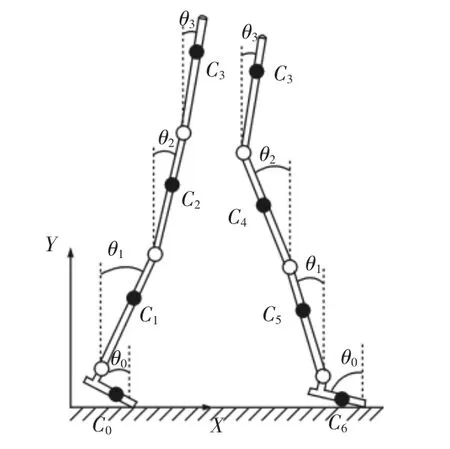
图5 双脚支撑行走模式Fig.5 Double Foot Support Walking Pattern

在这种行走模式下，如图5所示。双脚均处于与地面接触的状态，外骨骼和地面形成一个闭环链式结构。将闭环结构在上肢简化模型处分开形成两个多刚体的开环链式结构分别进行动力学分析。

两个开环链结构共同承担上肢的重量，可把上肢的质量m3分成mL3和mR3两部分，分别由左脚链和右脚链支撑。设L为两个脚踝关节的水平距离，上肢杆件的质心C3到左脚踝关节的水平距离可由式（6）计算得到，即 xC3，由式（11）计算得出 mL3。

对于左脚链模型，如图5所示。设左脚尖在绝对坐标系的坐标为（x0，0），则各个杆件质心Ci的坐标可表示为：

式中：i=0，1，2，3，cθ=cosθ，sθ=sinθ

下至外骨骼双脚支撑行走模式下各杆件受力模型，如图6所示。动力学模型的建立是从脚部到上肢，求解关节的扭矩则采用逆解法，即先求上肢的关节驱动扭矩，再逆向顺次求出各个关节的扭矩。

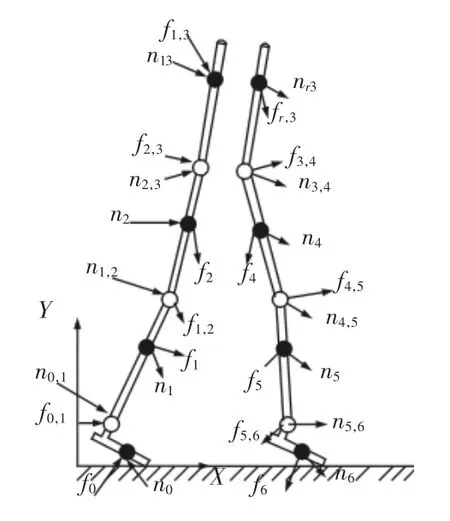
图6 双脚支撑动力学模型Fig.6 Dynamics Model of Double Foot Support

结合式（1）和式（4）、式（2）和式（5）建立杆件3的牛顿-欧拉方程为：

式中：fL3=是左脚链承担的人体上肢的质量，将运动学分析中求解的各关节的角速度、角加速度时间曲线，带入上式求出 f2，3，n2，3。同理，可以依次求出 f1，2、n1，2、f0，1、n0，1。

对于右脚链模型，其动力学分析步骤与左脚链动力学分析步骤基本一致，此处不再赘述。

5 动力学仿真分析

将下肢外骨骼简化模型导入ADAMS中进行动力学仿真，如图1所示。分析关节力矩与运动周期的曲线关系，同时在MATLAB中进行理论计算作为对比。

在ADAMS中将各关节设置为旋转副约束；将材料设置为铝合金，其杨氏模量为7.17×104MPa，泊松比为0.33，密度为2.71×102kg/m3；将髋关节、膝关节和踝关节的关节运动数据保存为.txt格式，导入ADAMS中，生成6个关节的Spline曲线函数，在6个关节的旋转副处设置旋转驱动，定义为 AKISPL（time，0，SPLINE_1，0）等[8-10]。

在仿真结果后处理中，选择各关节输出力矩和运动周期的关系曲线，对数据进行滤波处理。髋关节和膝关节的动态力矩的步态关系曲线，如图7所示。同时在MATLAB中将理论计算数据输出作为对比曲线。

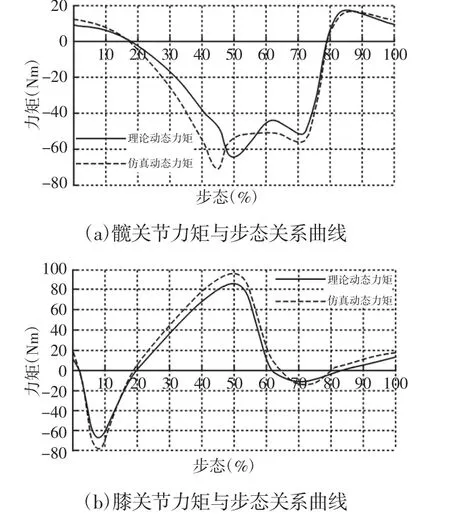
图7 力矩与步态关系曲线图Fig.7 Curve Relationship Between Torque and Gait

由图7可知，理论计算和仿真结果曲线存在一定的偏差，偏差在一定范围之内，属于合理偏差，同时也说明理论模型分析的正确性。分析理论计算和仿真结果产生偏差的主要影响因素为：理论计算过于理想化，将下肢外骨骼系统简化为七杆机构，而仿真中的模型结构相对复杂，此外，理论计算没有考虑人体、模型和环境之间复杂的接触力。

6 结论

（1）将人体下肢动力外骨骼简化为七杆机构，采用牛顿-欧拉方法分别对单脚支撑行走模式和双脚支撑行走模式进行动力学建模分析，求解出各关节的力矩，表明牛顿-欧拉方法是一种求解外骨骼机器人动力学模型的有效方法。

（2）在ADAMS环境下进行动力学仿真，求解出髋关节和膝关节力矩与运动周期的曲线关系，同时在MATLAB中进行理论计算作为对比，结果表明理论计算和仿真结果曲线存在一定的偏差，但基本一致。