非独立悬架参数变化对悬架系统特性影响分析

王 飞，李晓娜

（安阳工学院 机械工程学院，河南 安阳 455000）

1 引言

悬架是影响车辆行驶稳定性的重要结构，作为现代矿山开采运输的重要设备，矿用自卸车后悬架主要采取非独立悬架，形式主要包括A型架-横拉杆式，和四连杆式。目前大部分的车型比如Komatsu的630E、730E、830E、930E等都采用A型架-横拉杆结构。此种结构的A型架约束了后桥三个方向的位移自由度，主要承担纵向力，横拉杆约束的后桥横向的摆动，主要承担横向力，两个悬挂缸只承受垂直方向的力[1]。因此，此种结构形式简单而且可靠性高，应用较为普遍，对其运动学特性进行分析具有重要意义。尽管它应用广泛，但至今在设计中没有统一的准则，本章将通过对这种形式悬架的运动学特性进行分析，得到其设计准则。

对于悬架运动学特性的研究，国内外学者取得了一定的成果：文献[2]基于某微型车悬架的运动学特性搭建分析模型，并分析其对整车操纵稳定性的影响；文献[3]针对整车的操纵稳定性和平顺性对悬架的运动学特性影响参数进行优化设计；文献[4]基于虚拟样机技术对悬架性能进行分析，并研究其对整车操纵稳定性和平顺性的影响；文献[5]基于整车操纵稳定性模型，对汽车悬架系统进行稳健性设计。针对结构参数和位置参数对A型架-横拉杆式后悬架的运动学特性影响进行分析。根据悬架的结构特点和性能特征，基于R-W图论法建立其运动学模型，并针对这种非独立悬架建立其运动学特性的评价指标体系，对结构的运动学特性进行分析。利用参数扫描法，研究了横拉杆的长度、角度、安装方向以及A型架顶点的安装位置、初始安装角度等结构和位置参数对悬架的运动学特性的影响。

2 基于R-W图论法悬架运动学模型

A型架-横拉杆式是一种传统并广泛应用的矿用自卸车后悬架形式[6]。A型架约束后桥三个方向位移自由度，主要承担纵向力，横拉杆约束后桥横向摆动自由度，主要承担横向力，两个油气悬挂缸只承受垂直方向力。

2.1 系统运动学方程

A型架-横拉杆式悬架机构简图，如图1（a）所示。

图1 悬架机构简图及缩减Fig.1 Schematic Diagram of Suspension Mechanism and Reduction

图中：B0—车架，由于不考虑车轮滚动，且三角架焊接在后桥壳上，则B1代表后桥、三角架和车轮组合体，B2—横拉杆；B3—左侧悬挂缸缸筒；B4—左侧悬挂缸活塞杆；B5—右侧悬挂缸缸筒；B6—右侧悬挂缸活塞杆；h1—后桥与车架之间连接球铰；h2—横拉杆与后桥之间连接球铰；h3—左侧悬挂缸筒与车架之间连接球铰；h4—左侧活塞杆与左侧缸筒之间连接棱柱铰；h5—右侧悬挂缸筒与车架连接球铰；h6—右侧活塞杆与右侧缸筒之间连接棱柱铰；h7—左侧活塞杆与后桥连接球铰；h8—右侧活塞杆与后桥之间连接球铰；h9—横拉杆与后桥连接球铰。

根据图1（a）对有向图进行铰切除[7]，得到机构缩减系统有向图，如图1（b）所示。根据缩减系统有向图得其整数函数值，如表1所示。

表1 A型架-横拉杆悬架系统的整数函数值Tab.1 Integer Function Values of Suspension System

悬架机构完全关联矩阵S0和S分别为：

可知，减缩系统被刚体B0分为4个子系统：子系统1：B0-B1，关联矩阵 S1；子系统 2：B0-B2，关联矩阵 S2；子系统 3：B0-B3-B4，关联矩阵S3；子系统4：B0-B5-B6，关联矩阵S4。均为有根树形系统。通路矩阵T为：

式中：T1，T2，T3和 T4—四个子系统通路矩阵。

图2 系统体铰矢量图Fig.2 Body Hinge Vector Diagram of the System

O、H、I、J点坐标是计算悬架运动学特性关键参数，需首先得到任意时刻四个点坐标值[8]。假设O点为刚体B1质心C1，H点，I点和J点为数值计算点，另假设C点和E点是两侧活塞杆质心C4和C6，假设沿着缸筒轴线方向单位长度位置为缸筒质心C3和C5，假设F 点为横拉杆质心 C2，再补充矢量 loI，loH，lJH在计算C 点和D点坐标时使用。假设h4和h6位置分别在C3和C5，所以c34和c56为0，系统体铰矢量，如图2所示。

子系统1，体铰矢量矩阵和通路矢量矩阵为：

则，系统运动学关系：

式中：k—子系统标号，1、2、3、4；［r］k由 Bi刚体质心位置矢径 ri构成列阵；r0—刚体 B0质心矢径；［1］—元素为 1 的（n×1）维列阵；［D］—通路向 dij构成的（n×n）矩阵。

2.2 运动学特性指标

利用运动学模型，主要研究以下特性指标在悬架运动过程中的变化：后桥中心侧向位移；后桥中心纵向位移；后桥中心垂向位移；俯冲角（和后倾角正负号不同）；后桥侧倾角；后桥侧倾转向角[9]。上述指标可由以下关系求得，其为后桥中心在运动过程中瞬时坐标，（xo、yo、zo）为后桥中心初始坐标。

所研究悬架硬点坐标，如表2所示。

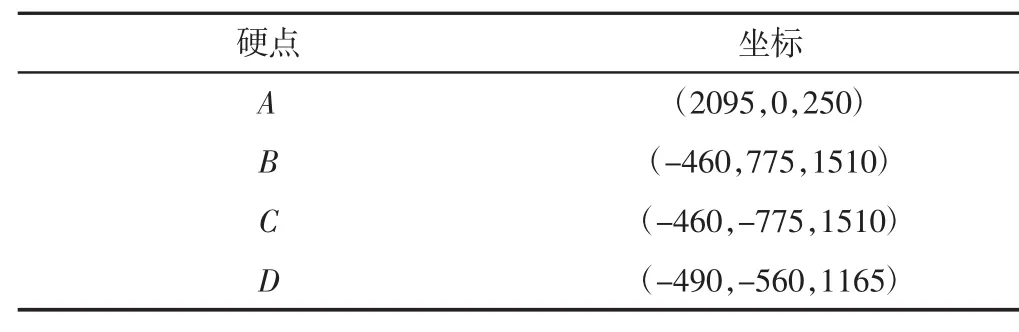
表2 A型架-横拉杆式悬架的硬点坐标Tab.2 Hard Point Coordinates of Suspension

3 悬架特性分析

3.1 平行轮跳运动学特性

平行轮跳即左右油气悬挂同步伸缩，伸缩行程与前悬挂相同：（-190～80）mm，拉伸为负，压缩为正。如图 3 所示。

图3 后桥中心纵向位移Fig.3 Analysis Results of Parallel Wheel Jump

后桥中心侧向位移变化范围（-23～+17）mm，压缩行程向y轴正向（左）移动，拉伸行程向右移动。纵向位移变化范围为（-11～+7）mm，压缩行程向x轴正向（前）移动，拉伸行程向后移动。观察后桥中心垂向位移范围发现，悬架行程对应压缩：（0～-80）mm，拉伸：（0～190）mm，而后桥中心垂向位移范围为压缩：（0～-50）mm，拉伸：（0～130）mm。可见对于后悬架而言，行程并不对应着后桥垂向位移行程，结合四个轮心垂向位移来看，由于这种悬架不对称性，四个轮心跳动不是完全同步的，但是差值很小，在拉伸行程极限处也保持在2mm以内，轮跳和悬架行程也不是对应的，这种型式悬架可控制轮跳行程。

3.2 反向轮跳运动学特性

反向轮跳对应两侧悬挂缸异步伸缩，当一侧拉伸至最长时，另一侧压缩至最短，考察后桥运动学特性变化，如图4所示。

图4 反向轮跳分析结果Fig.4 Reverse Wheel Jump Analysis Results

由图可知，悬架最大行程对应后桥侧倾角变化范围（-10～10）°。相应后桥中心侧向位移变化范围（-160～130）mm，可见侧向位移变化较大。反向轮跳过程中，纵向位移变化范围小，最大1.25mm，可见对后桥纵向位移控制较好。后桥中心垂向位移在侧倾极限处约为50mm，后桥侧倾转向角在向左侧倾时变化范围（0～2.7）°，在向右侧倾时（0～-3.5）°，后桥这种侧倾转向特性不能被忽略。

4 参数变化对运动学特性影响

4.1 横拉杆长度

横拉杆在车架安装点设为固定点，在后桥上安装点设为可动点，保证横拉杆角度为0，只变动y向坐标，横拉杆长度分别为560mm、710m、1060mm、1310mm、1560mm，对应后悬架同向轮跳特性，如图5所示。

图5 横拉杆长度的影响Fig.5 The Influence of the Length of the Tie Rod

横拉杆长度主要影响后桥中心侧向位移，而纵向位移和俯冲角变化范围均很微小。观察后桥中心侧向位移变化曲线，当横拉杆安装角为0时，越长的横拉杆使得后桥在同向轮跳时侧向位移变化最小，以拉伸至极限位置为例，长度为1560mm横拉杆对应位移最大值为8mm，而长度为560mm横拉杆对应位移最大值为21mm。

对应悬架进行反向轮跳运动学分析，横拉杆长度对后桥中心侧向位移、纵向位移以及后桥侧倾转向角影响都极小。

4.2 横拉杆角度

横拉杆角度是指当自卸车处于重车位置时，横拉杆与车辆坐标系Y轴夹角[10]。仍取车架安装点为固定点，后桥安装点为可动点，y向坐标取原始设计值，而 z向坐标选择 200、100、0、-100、-200进行分析，ZF每变化100mm对应横拉杆角度变化大约是5°，故横拉杆角度为：-10°、-5°、0°、5°、10°，平行轮跳结果，如图 6 所示。

图6 横拉杆角度的影响Fig.6 Influence of the Angle of Tie Rod

由图可知，横拉杆角度主要影响平行轮跳时后桥侧向位移值，0°时，侧向位移变化范围最小，角度增加会使后桥中心侧向位移增大。纵向位移差距在悬架行程极限处也大约不过0.1mm，垂向位移差距大约在0.5mm。横拉杆角度对平行轮跳时后桥纵向和垂向位移影响微乎其微，反向轮跳，如表3所示。

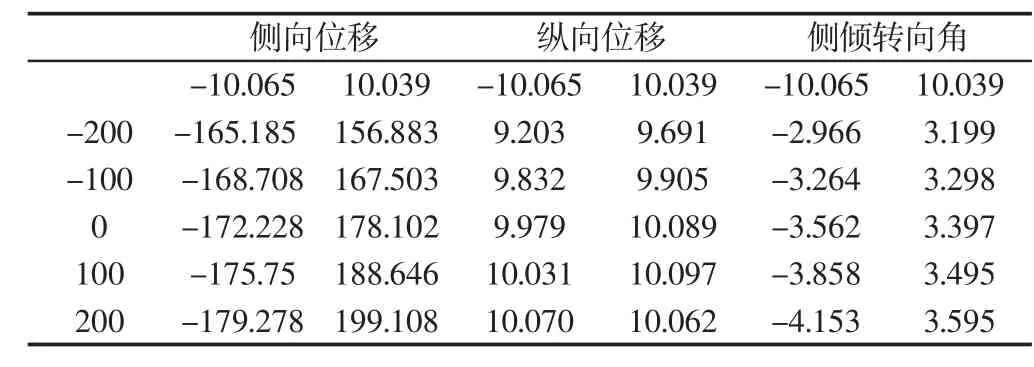
表3 横拉杆角度影响Tab.3 Influence of the Angle of Tie Rod

由于数值相差不大，表中仅列出左右侧倾到极限位置处侧向位移、纵向位移和侧倾转向角数值。对后桥中心侧向位移而言，横拉杆角度越大，侧向位移变化越小，以侧倾角10°为例，-200对应侧向位移为156.833mm，而+200对应侧向位移则达到199.108mm。而对于后桥中心纵向位移而言，角度越小，纵向位移极值会减小，但是减小幅度非常少，可忽略。对于后桥侧倾转向角而言，横拉杆角度越大，侧倾转向角越小，在后桥侧倾角为-10°时，-200对应侧倾转向角为2.966°，而+200对应侧倾转向角为4.153°，可见在极限位置时，越“斜”横拉杆越能使后桥后倾转向趋势减弱。

4.3 横拉杆安装方向

横拉杆安装方向是指从自卸车后方向前方看，如果横拉杆在后桥上安装点位于左侧，在车架上安装点位于右侧，称为“左桥右架”，如果横拉杆在后桥上的安装点位于右侧，而在车架上的安装点位于左侧，则成为“右桥左架”。

平行轮跳结果，如图7（a）所示。主要变化的是后桥中心侧向位移，两种安装方向对应后桥侧向位移曲线相对于悬架行程坐标轴对称，可见，安装方向不能改变侧向位移数值大小，只能改变在压缩或拉伸行程时，后桥中心侧向位移方向。

反向轮跳结果，如图7（b）所示。其中，侧向位移曲线关于原点对称，可见，不同横拉杆安装方向对应悬架特性不对称性，由于横拉杆，平行轮跳和反向轮跳过程中悬架特性都是不对称的，而不同安装方向使得变化不对称性偏向某一边，所以采取两种安装方向中任何一种都无法消除不对称性，而二者在设计中均可采用。

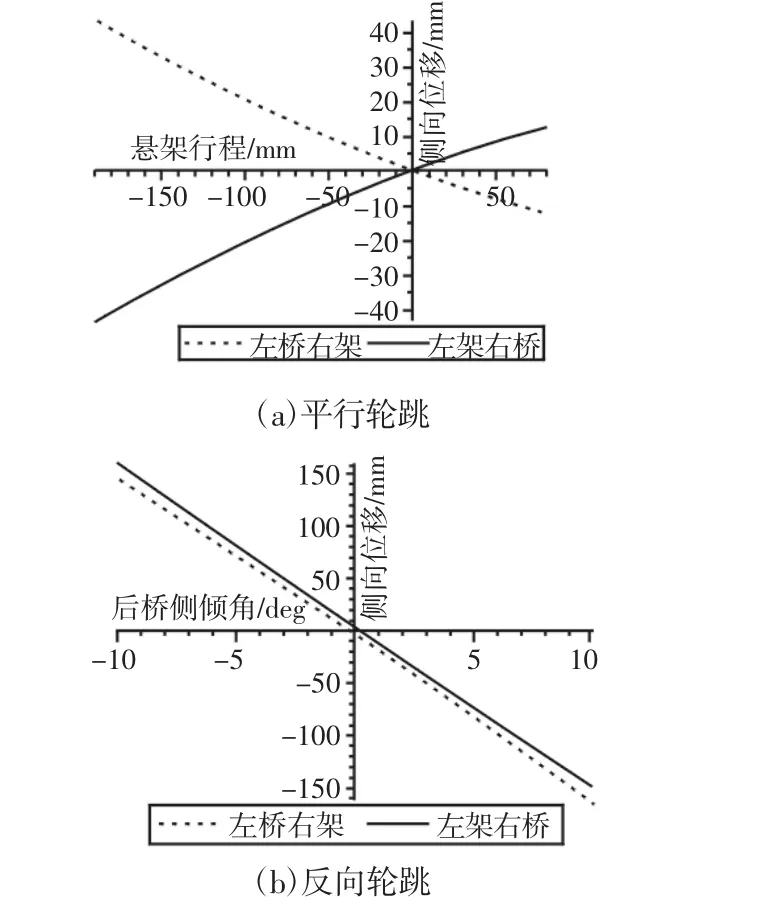
图7 横拉杆安装方向对后桥侧向位移的影响Fig.7 Influence of the Installation Direction of the Tie Rod

4.4 A型架顶点纵向位置

A型架顶点安装在纵向对称面上，因后桥侧倾和纵倾都以这一点为基准，故顶点y向坐标为0，但具体安装位置，即坐标x和z值没有明确设计准则，一般选取车架中部抗扭管下方为安装点。使A型架顶点z向坐标固定不变，变化x向坐标，以初始设计值为0，x朝后变化（-100）mm，（-200）mm，朝前变化 100mm，200mm，平行轮跳、反向轮跳结果，如表4、表5所示。

表4 平行轮跳时 A型架纵向长度对后桥运动的影响Tab.4 Effect of A-Type Frame Length

表5 反向轮跳时A型架纵向长度对后桥运动的影响Tab.5 Effect of A-Type Frame Length

可以看出，A型架纵向位置对于平行轮跳时后桥运动影响较小。纵向位置越靠前，后桥中心侧向位移在极限位置处数值越大，而纵向位移和俯冲角则刚好与侧向位移变化相反，A型架顶点纵向位置越靠后，后桥纵向位移和俯冲角在油气悬挂拉伸或压缩到极限位移时的数值越小。

后桥侧倾时，A型架顶点纵向位置越靠后，后桥中心侧向位移在侧倾到极限位置时数值越小。而对于后桥中心纵向位移和后桥侧倾转向角而言情况却不同，不论后桥是向左还是向右侧倾，后桥中心纵向位移数值都是先增大后减小，A型架顶点纵向位置越靠后，纵向位移增大极值点数值就越大，侧倾转向角在后桥侧倾到极限时数值也越大。

4.5 A型架顶点垂向位置

A型架顶点垂向位置选择，会影响到重车位置时A形架顶点与后桥中心连线角度。平行轮跳结果，如图8（a）所示。反向轮跳结果，如图 8（b）所示。

图8 A型架顶点垂向高度对后桥运动的影响Fig.8 Influence of the Vertical Height of the A Shaped Frame

由图可知，A型架顶点垂向位置对后桥中心侧向位移影响很小，对纵向位移影响较为明显。在“0”位置处，即顶点与后桥中心连线角度为0时，纵向位移变化幅度最小。顶点垂向位置对后桥中心纵侧倾转向角有较明显影响，垂向位置越高，后桥中心纵向位移和后桥侧倾转向角变化越小。

5 结论

基于R-W图论法建立A型架-横拉杆式后悬架运动学模型，并针对这种非独立悬架建立其运动学特性评价指标体系。利用参数扫描法，研究横拉杆长度、角度、安装方向以及A型架顶点安装位置对其运动学特性影响。可知：

（1）A型架-横拉杆式悬架运动学特点是平行轮跳和反向轮跳时，后桥中心侧向位移变化较大，纵向位移变化较小，A型架-横拉杆式悬架轮跳行程小于悬架行程，对轮胎垂向跳动有控制作用。

（2）横拉杆长度增加时，同向和反向轮跳中后桥各向位移均减小。增大横拉杆角度可使后桥后倾转向趋势减弱。不同横拉杆安装方向只是使得这种形式悬架运动学特性变化不对称性偏向某一边而已，采取两种安装方向中任一种都无法消除不对称性，而二者在设计中均可以采用。

（3）A型架纵向位置对不同参数变化影响不同，在设计时取适中位置即可。其垂向位置对平行轮跳和反向轮跳时纵向位移和侧倾转向角有较明显影响，垂向位置布置较高一些可减小纵向位移和侧倾转向角变化。