设备频谱预测的全矢-GM(1,1)方法研究
官振红,赵伟杰,陈 磊,韩 捷
(郑州大学 振动工程研究所,河南 郑州 450001)
1 引言
设备故障预测就是要通过技术手段,预测在未来的一定时间内机组的运行状态,预知将要发生的设备故障,以便指导生产调度和设备维修。当前,国内外学者对于故障预测的研究主要集中于故障强度、剩余寿命和有无故障方面[1-3],多以事先确定的某种特定的单一故障展开,而对于故障性质和类型的预测则相对较少[4-5]。要对故障类型和性质进行预测,就需要对设备振动信号的频谱结构的发展趋势进行预测,并根据预测所得的频谱结构判断机组的故障性质和类型[6]。
从采集到的振动信号中如何有效提取出反映故障发展趋势的特征量一直是旋转机械故障预测的核心和难点。转子系统的振动信号一般由安装在转子同一截面相互垂直的两个传感器进行采集。不同方向采集到的振动信号进行频谱分析时,发现频谱结构存在差异性,因此,仅仅依靠单源信号进行预测,很难反映出机组的运行状态。为提高旋转机械故障预测的可靠性,对不同方向的振动信息进行融合则很有必要。基于同源信息融合的全矢谱技术很好的解决了这个问题,将全矢谱技术引入预测模型是多传感器信息融合技术在设备故障预测中的典型应用,可有效的避免单源信号故障特征提取不完整的弊端,完整的表述转子在整个截面内的振动状态。
基于数据的预测包含时间序列预测、灰色预测、支持向量机预测、神经网络预测、混沌预测等方法[8]。其中灰色预测方法以其在小样本、贫信息、不确定问题上的研究应用而受到关注。当前学术界对灰色预测模型的研究绝大部分集中在对GM(1,1)模型的优化上,形成了以灰色生成技术为基础,GM(1,1)模型为核心的灰色预测模型体系。有鉴于此,提出一种基于全矢幅值谱的GM(1,1)预测方法,对旋转机械转子系统的频谱结构进行预测研究。
2 全矢—GM(1,1)模型理论
2.1 全矢谱理论
旋转机械的振动测量,一般采用非接触的电涡流传感器测量其转子相对位移,传感器安装采用垂直-水平或V形安装方式,如图1所示。平稳运行的机组,两支传感器获取的转子振动,是在传感器安装平面内若干谐波wi(i=1,2,…)下的稳态涡动的组合。
对某一谐波i,假定:

式中:Xi、Yi—谐波 i在 x、y 方向振动信号的振幅;
φxi、φyi—谐波 i在 x、y方向振动信号的相位角。
x、y向的运动方程式一般可以表达为:
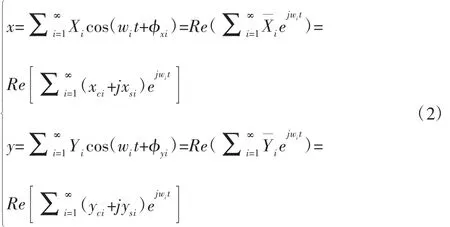
动轨迹为一个椭圆,即:
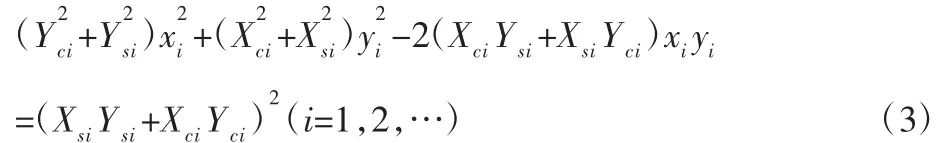
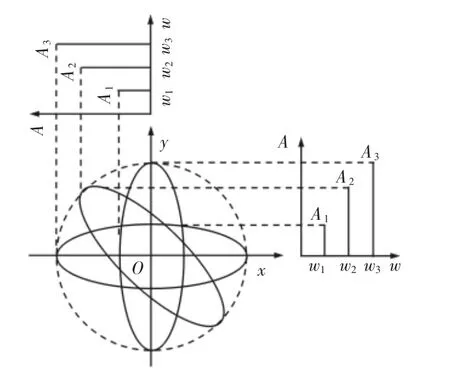
图1 不同方向安装传感器时的频谱结构误差Fig.1 Spectral Structure Error of Sensor in Different Direction
假设某个振动谐波的角频率分别为w1、w2和w3,对应谐波的椭圆长轴为A,长轴与x方向之间的夹角分别为0、π/4和π/2,如图1所示。从图中可以看出,采用单一传感器测量时,同样的振动源产生的信号,用安装在x方向和y方向的传感器,将会测得截然不同的频谱结构。也就是说,不管是x方向还是y方向的测量结果,所反映的转子振动状态都是片面的,甚至在不同方向上得出的是完全不同的结果。用这样的信号进行故障诊断和故障性质预测,其诊断结论的可靠性无法得到保障。若要得到可靠的预测和故障性质判定结果,就需要克服单个传感器振动信息的片面性,在数据层进行多传感器的融合。
假定时间序列{xi}、{yi}分别为同一截面互相垂直方向即x、y方向上采集的离散信号,其中 i=0,1,2,…,N-1,N 为采样点数。将同步整周期采集到的x和y通道数据合成为复数序列{zi},即zi=xi+jyi,对复数序列{Zi}求FFT变换得到{Zk},其中,k=0,1,2,…,N/2-1。全矢谱理论认为各振动谐波下主振矢、副振矢等参数的复杂计算可以简化为傅里叶参数之间的简单计算。式(1)中,RLk和RSk分别为主振矢和副振矢。振动各个谐波频率的主振矢为谐波涡动椭圆长轴的大小,可以表征在该谐波频率下的振动值的大小,其与传感器的安装位置无关,是振动强度的真实反映,可以用全矢幅值谱判定故障性质、故障类型。将按时间序列测得的振动信号的全矢幅值谱作为特征向量送入预测模型,可以进行趋势预测和故障性质判断。
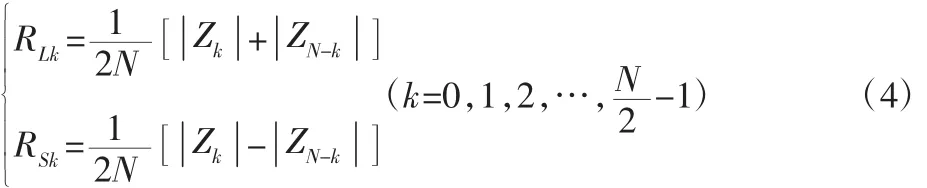
2.2 GM(1,1)模型
灰色预测理论建模所需数据量少,且在中短期预测中优势突出。GM(1,1)模型是灰色预测中最常用的模型,建模对象主要是具有指数或者近似指数增长规律的序列。它通过对原始序列进行累加,生成规律性较强的新序列,再用指数曲线去拟合得到预测值。设X(0)为原始数据序列:

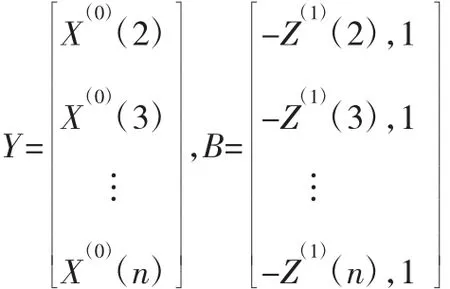

得到的离散化预测模型为:
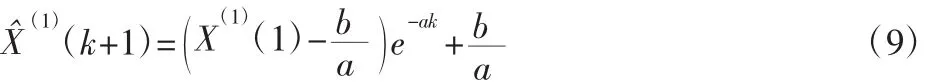
由式(6)得到原始序列的预测模型为:
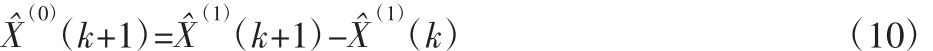
3 全矢 -GM(1,1)模型的建立
基于全矢谱技术和GM(1,1)模型的预测模型建立方法如下:
(1)在风机设备轴承座上互为90°方向布置2枚磁吸式压电加速度传感器,采得M组同源双通道振动信号,每组信号长度为N,存为数组{xij},{yij}(i=0,1,2,…,M-1;j=0,1,2,…,N-1)。
(2)运用全矢谱技术构建数组{zij}={xij}+j{yij},对每一行做FFT 求得{Zik}(i=0,1,2,…,M-1;j=0,1,2,…,N-1),由式(1),求得各组数据主振矢频谱序列组{Rik}(i=0,1,2,…,M-1;k=
(3)提取每组数据1X,2X,3X,4X,5X 的主振矢幅值,构建各个倍频下幅值序列{Ami}(m=0,1,2,3,4;i=0,1,2,…,U-1),提取各倍频幅值序列的前U个数据作为原始数据,重新构建幅值序列{Tmn}(m=0,1,2,3,4;n=0,1,2,…,U-1),剩余 M-U 个数据作为预测验证数据。
4 实验研究
在平顶山鲁阳发电厂2号汽轮机轴承座上采集运行数据,实验步骤如下:
(1)在轴承座水平、竖直方向上进行同步整周期数据采集,其中高压转子转速为3000r/min,采样频率为1600Hz,采样长度为1024点,并按预定的时间间隔(每隔4h取一组数据)连续采集数据45组。以前40组数据作为已知数据,后5组数据作为预测验证数据。
(2)通过全矢谱技术求得每组数据的主振矢频谱,观察全矢幅值谱图找出幅值较高的频谱横坐标作为谱图的敏感频带,提取敏感频带的幅值,构成倍频序列,这里取1倍频、2倍频、3倍频、4倍频、5倍频。
(3)将各倍频下的重构幅值序列{Tmn}(m=1,2,3,4;n=0,1,2,…,39)送入 GM(1,1)模型,并预测 5 步序列值,与实际值进行比较。
敏感频带在GM(1,1)模型下五步预测的实际值、预测值和相对误差,如表1~表3所示。可以看出,一步预测时,在一倍频上表现出了最高预测精度,达到0.16%,四倍频的预测精度最低,为7.77%;三步预测时,一倍频到四倍频上表现出的精度都在(6~7)%之间,五倍频上略高,达到9.88%,但仍在可接受范围内。五步预测时,一倍频、四倍频上误差稍大,分别为9.51%、9.98%,其余都在9%以下。综上所述,各特征频率在5步内预测上均表现出较高的精度,5步预测相对误差均小于10%。其中,一步、二步、三步、四步、五步预测的平均相对误差分别为3.62%、5.56%、7.11%、7.56%和8.93%。随着预测步数的增加,平均相对误差逐渐增大。一般认为3步内预测为有效,且相对误差须控制在10%以内,该方法3步内预测的平均相对误差为7.11%,在可接受范围之内,可以满足工业现场应用需要。作出汽轮机转子测量的预测和实际全矢幅值谱瀑布图,如图2、图3所示。
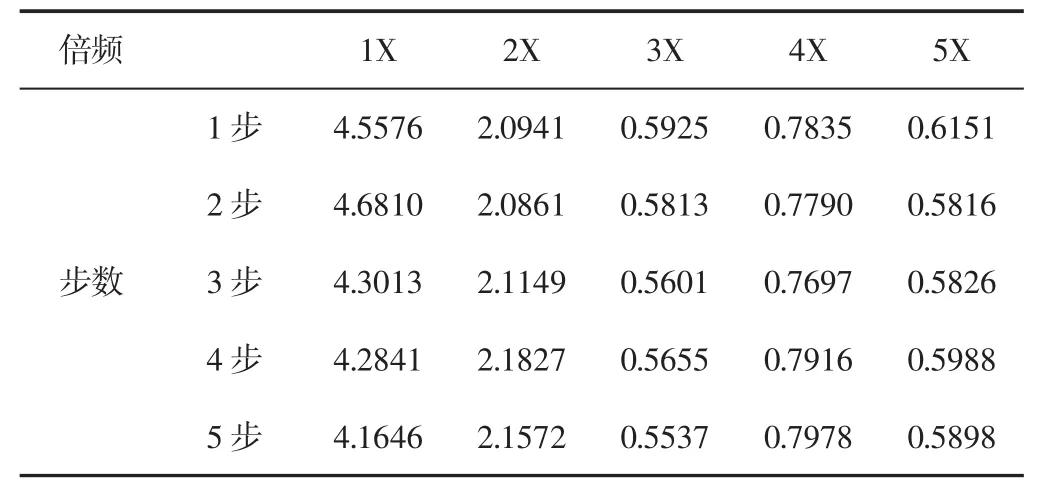
表1 五步预测主振矢实际值Tab.1 Five Step Prediction of the Actual Value of the Main Vibration Vector
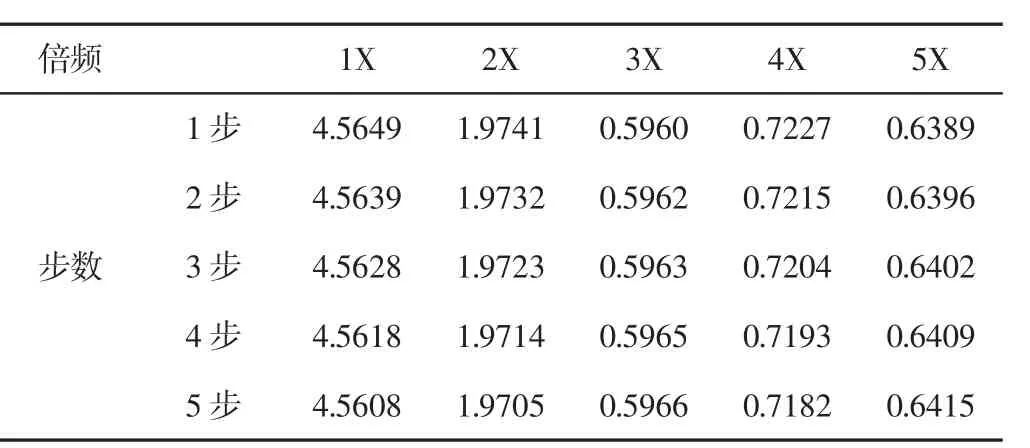
表2 五步预测主振矢预测值Tab.2 Five Step Prediction of the Forecast of the Main Vibration Vector
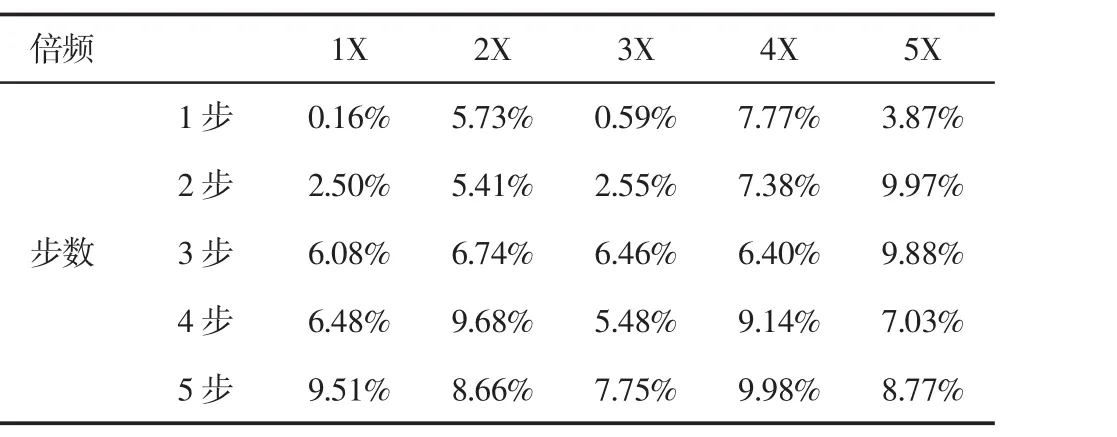
表3 五步预测主振矢相对误差Tab.3 Five Step Prediction of the Relative Error of the Main Vibration Vector
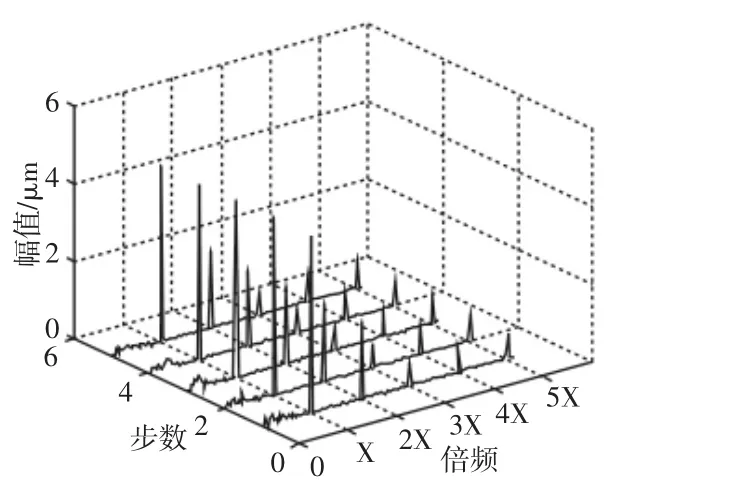
图2 预测值频谱结构图Fig.2 Spectrum Chart of the Predicted Value
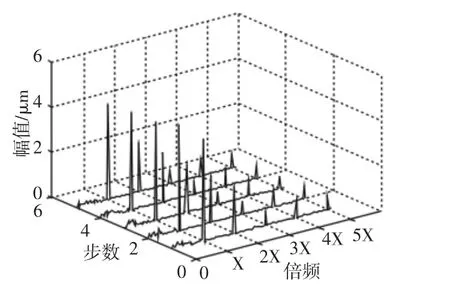
图3 实际值频谱结构图Fig.3 Spectrum Chart of the Actual Value
各倍频成分趋势预测结果,如图4~图6所示。对比图2和图3的频谱结构(全矢幅值瀑布图),我们可以从直观上感受机组的运行状态。不同故障类型往往表现出的不同频谱结构,比如不平衡故障在一倍频上幅值会明显高于其它倍频;不对中故障在二倍频上幅值最大,并常伴有一、三倍频。因此,对谱结构的预测变得尤其必要。预测谱结构可以预判故障类型进而知晓故障位置,及时排除隐患。
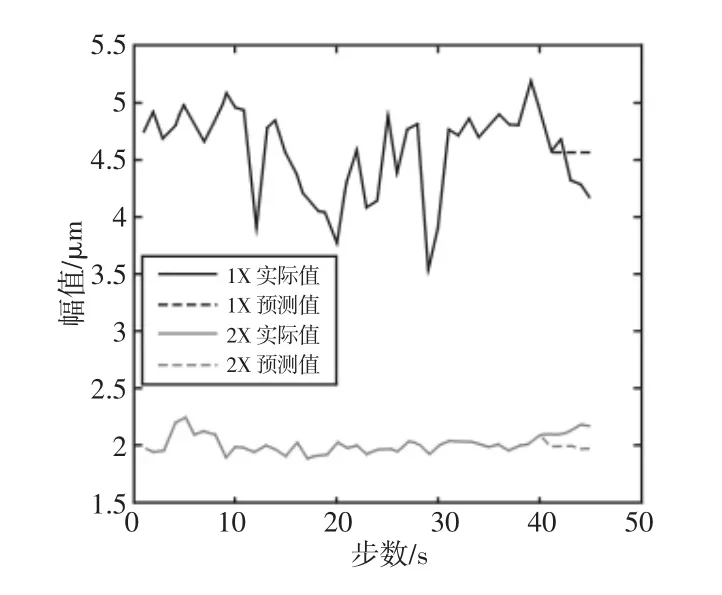
图4 1X、2X趋势预测图Fig.4 Trend Forecast Figure of 1X、2X
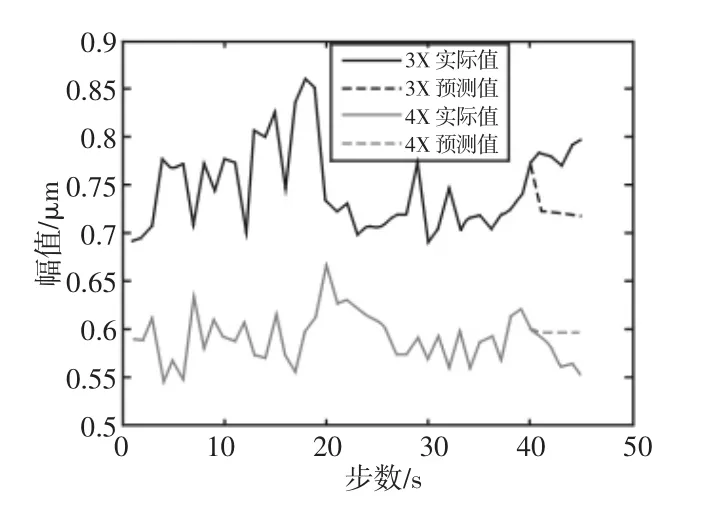
图5 3X、4X趋势预测图Fig.5 Trend Forecast Figure of 3X、4X
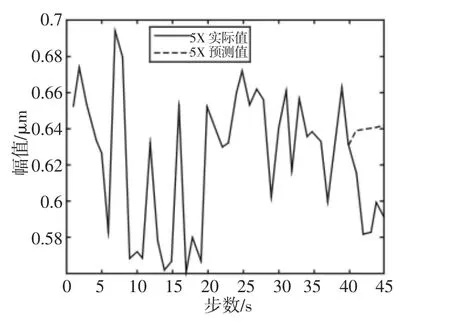
图6 5X趋势预测图Fig.6 Trend Forecast Figure of 5X
5 结论
对旋转机械振动信号的频谱结构进行预测,可以有效判定设备故障的类型和性质。为提高故障预测的可靠性,提出一种基于全矢-GM(1,1)模型的预测方法,首先以全矢谱技术提取故障特征,有效保证了频谱结构的唯一性。其次选用对趋势变化敏感的灰色GM(1,1)模型,可有效对特征频率变化趋势进行跟踪。实验以汽轮机转子为分析对象,对其由全矢幅值谱得到的频谱结构进行5步内预测。实验结果表明,该方法能较准确地对敏感频带幅值序列进行预测,能准确地反映出未来的频谱结构,可以有效满足工厂上实时性的需要,对进行模式识别预判故障类型具有重要意义。

