遗传离散粒子群算法求解车辆货物配装问题

牛江川，刘 凯，申永军，韩彦军

（石家庄铁道大学 机械工程学院，河北 石家庄 050043）

1 引言

随着信息技术的发展，企业面临的生存与发展环境日趋复杂。物料配送车辆在进行货物配装时，目前常依靠经验，进行估算配装，没有预先进行统一的设计，低效的空间利用率和混乱的货物摆放等问题严重影响货物配装效率，甚至装卸需要多次尝试才能完成配装，从而导致人力和财力的浪费，企业必须不断地采用创新的理念与技术，才能为生产部门和运输部门带来效益。

货物配装是一个有约束条件的离散组合优化问题，求解体积或重量的最优利用率，研究方法主要有精确算法、启发式算法和智能算法。精确算法只能有效求解中小规模问题，在可以求出结果前提下，可以获得比人工智能算法更优的解[1]。启发式方法缺乏全局寻优能力，尤其是在求大规模问题时效率不高[2]。当求解大规模多约束条件的复杂问题时，智能算法应用更为普遍。文献[3]采用改进模拟退火算法依靠降温策略求解了单一品种和多品种货物配装问题。文献[4]通过对遗传算法设计改进求解铁路集装箱运输中多类型普零货物的配装问题，优化了装载结果，并对遗传算法解决该类货物配装问题的可行性给予了证明。文献[5]用蚁群算法求解双目标散货配装模型求解单货车的载重和容积利用率最大问题，在求解速度和准确度方面均有提高。文献[6]采用标准粒子群算法，将超载惩罚函数加入到粒子适应度的计算中，同时提出合并优化策略，使粒子的局部优化能力有所提高。将遗传算法和离散粒子群算法的思想结合起来，将交叉和变异步骤加入到离散粒子群算法粒子速度和位置的更新之中，采用遗传离散粒子群算法求解货物配装问题。

2 数学模型

设有j（j=1，2，3，…，m）个体积和重量均不相同的货物，gj为货物j的重量，cj为货物j的体积，容积为C、载重为G的货车，研究货物如何配装才能合理利用车厢容积和载重。

假设前提条件如下：

（1）装箱货物无优先级；

（2）货物体积不可压缩，为外径体积；

（3）货物为直接送往同一个地点；

（4）假设每类货物体积和重量均不相同，实际情况体积和重量相同的货物可归为一类。

则可以得到目标函数：

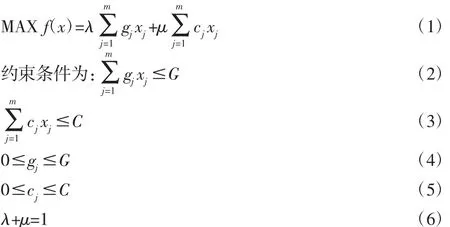
式中：λ∈（0，1），当 λ=1 时，表示求载重量最大；μ∈（0，1），当 μ=1时，表示求容积利用率最大；xj—一个01变量，当xj取值为0时，表示这一批次的货物配装不装货物j，反之，当xj取值为1时，表示这一批次的货物配装需装货物j。若最优解为（1，0，1，0，…）表示要装载的货物为 1，3，…。

3 遗传离散粒子群算法

3.1 离散粒子群算法

设D维搜索空间中，n个粒子组成一个群体，每个粒子都具有位置和速度两个特征，每个粒子都表示搜索空间中的一个潜在的可行解，其中，第 i个粒子的位置记为 Xi=（xi1，xi2，…，xiD），i=1，2，3，…，n，速度记为 Vi=（vi1，vi2，…，viD），该粒子经过搜索，得到的最优位置即最优的适应度值记为 pi=（pi1，pi2，…，piD），也称 pbest。在粒子群体中，所有粒子经过的最优位置记为pg，也称为gbest。当粒子找到个体极值（pbest）和全局极值（gbest）时，根据式（7）来更新当前粒子的速度。

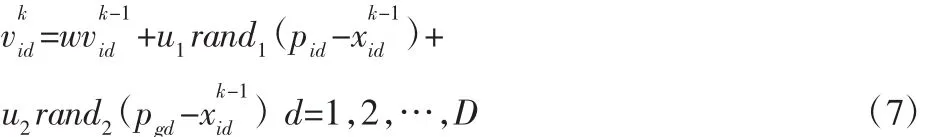
式中：w—惯性权重；u1、u2—加速度系数；rand1、rand2—［0，1］间取值的随机数；vkid—第k次迭代粒子i飞行速度矢量的第d维分量；pid—粒子i个体极值的第d维分量；pgd—全局极值的第d维分量。

由于粒子位置的每一维只有0和1两种取值，将粒子设计为一个XnD的0-1矩阵，为了表示速度值是二进制位取1的概率，速度值采用Sigmoid函数被映射到区间［0，1］上，故根据式（8）、式（9）改变粒子的位置。

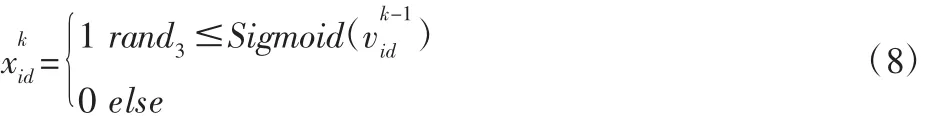
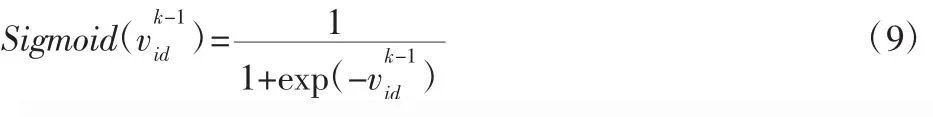
式中：xid—第k次迭代粒子i位置矢量的第d维分量，xid=1—装货物 i，xkid=0 则表示不装货物 i。rand3—［0，1］间的随机数，位置更新依赖于粒子速度决定的状态转移概率，速度大于一定的数值，粒子取1的可能性大，反之，取0的可能性大，且这个数值为［0，1］间的随机数。

从上述粒子速度、位置更新策略可知，粒子某一位取1的概率为 Sigmoid，取 0 的概率则为 1-Sigmoid，由此可得到粒子某一位发生变化的概率：

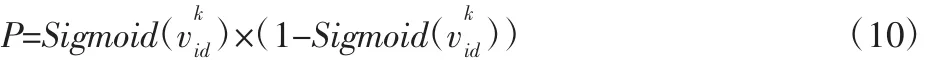
3.2 交叉变异策略

保持种群多样性有利于种群进化，借鉴遗传算法中的交叉变异操作，增加粒子的多样性，是避免种群陷入局部最优死循环的有效手段。当种群全局极值连续10次迭代没有发生变化时，则认为种群陷入了局部最优解[7]。

在结束了上一次迭代后，根据粒子目前的最优适应度值，从粒子中选出适应度最好的全局最优粒子，后随机选择另1个与全局最优粒子配对的粒子，然后在个体编码串中选择2个交叉点，第1个位置在［1，D/2）内随机选择，第2个位置在（D/2，D］内随机选择，最后将两个粒子中2个交叉点之间的编码互换，得到新的粒子，如图1所示。对这一代得到的新粒子，采用优秀个体保留的策略，当新得到的粒子适应度优于交叉前的粒子才更新粒子，否则上一代的全局最优粒子将直接保存到下一代。

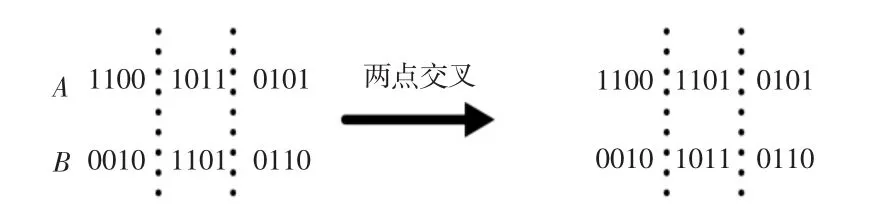
图1 交叉操作Fig.1 Crossover Operation

在交叉过程中，为了增加粒子群粒子的多样性，避免一些优良因子由于交叉被替换出粒子群，引入变异操作，以取值低于0.01的概率对粒子中的因子进行取反操作，新产生的粒子有益于保持粒子群的多样性。低于0.01变异概率意味着交叉后的粒子因子取反的可能性很低，产生不良因子的概率很低，如果交叉后产生不良因子，通过适应度值的对比也可以将其替换出粒子群。

3.3 参数分析

遗传粒子群算法的参数包括搜索空间维数D、种群规模N、惯性权重 w、加速度系数 u1、u2。

（1）搜索空间维数D：搜索空间维数D是由所求解问题解的长度确定的，一般为目标函数中未知数的个数。

（2）种群规模N：种群规模N一般取搜索空间维数D的5倍。

（3）惯性权重w：惯性权重系数w越大，算法的全局搜索能力就越强，但求解精度低，而较小的惯性权重系数w能加强算法的局部搜索能力求解精度高但求解速度慢。惯性权重系数w一般在（0.1～0.9）间取值[8]，实验表明，当 w=0.6 和 w=0.729 时，算法性能较佳。

（4）加速度系数 u1、u2：加速度系数 u1、u2代表了粒子向个体极值pbest和全局极值gbest推进的最大步长[9]。加速度系数太小，会使粒子在远离目标区域内振荡，而加速度系数太大，又容易越过目标区域，所以，理想的加速度系数不但有利于目标函数的收敛，而且可避免算法陷入局部最优无法跳出。当u1=（2.75～1.25），u2=（0.5～2.25），大多数目标函数都可以得到较好的适应度值。

3.4 算法实现流程

遗传粒子群算法具体实现步骤如下：

（1）参数给定，给定群体个体数目N、搜索空间维数D、算法重复次数HX、最大迭代次数MaxDT、惯性权重w、加速度系数u1、u2。粒子种群位置X、速度V的初始化，生成初始解。

（2）计算种群的适应度值fitness。

（3）根据粒子适应度值的计算结果，更新粒子的个体极值pbest和全局极值 gbest。

（4）根据得到的个体极值 pbest、全局极值 gbest以及式（7）、式（8）、式（9）更新粒子的速度和位置。

（5）选择、交叉、变异操作。

（6）计算新产生种群的适应度值fitness。

（7）对比新产生种群的fitness与上一代种群的fitness，若新产生的粒子的fitness优于当前种群的fitness，那么新粒子替换当前粒子，否则粒子的路径信息不更新。

（8）根据适应度值更新个体极值pbest和全局极值gbest，并判断循环条件是否达到，若达到，输出最优解，算法结束，否则，返回（2）。

遗传粒子群算法具体实现流程图，如图2所示。

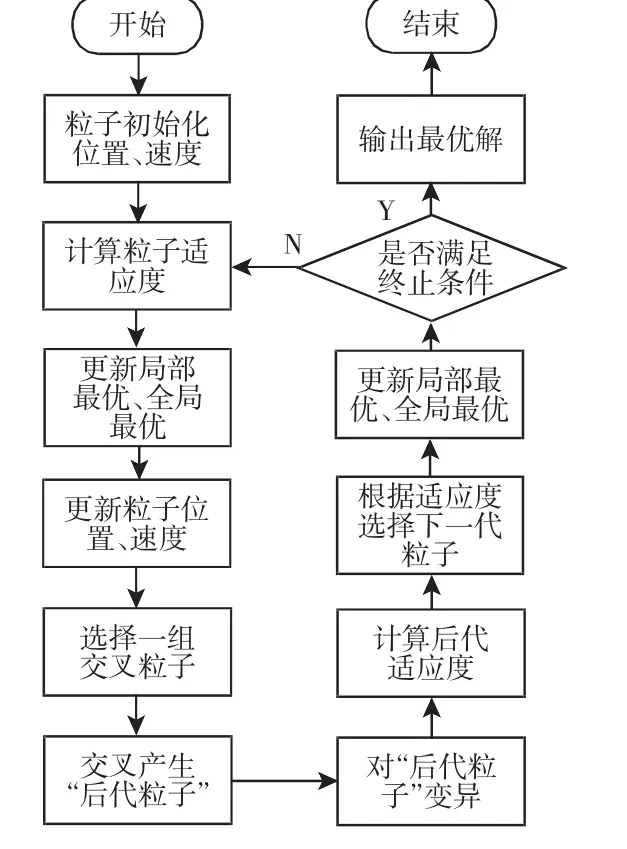
图2 遗传离散粒子群算法流程图Fig.2 Flow Chart of Genetic Discrete Particle Swarm Optimization Algorithm

4 算例求解

算例数据取自文献[10]，某载重量为30t的箱式货车，车厢内容积为70m3，要对14种货物选择配装，各种货物的重量、体积，如表1所示。求出合理的货物装箱结果。采用遗传离散粒子群算法和基本粒子群算法对上述货物配装算例在Matlab中求解，主要参数设置如下：群体个体数目N=70、搜索空间维数D=14、算法重复次数HX=10、最大迭代次数MaxDT=300、惯性权重w=0.729、加速度系数u1=1.49445、u2=1.49445。两种算法平均运行10次，具体优化配装结果，如表2、表3所示。

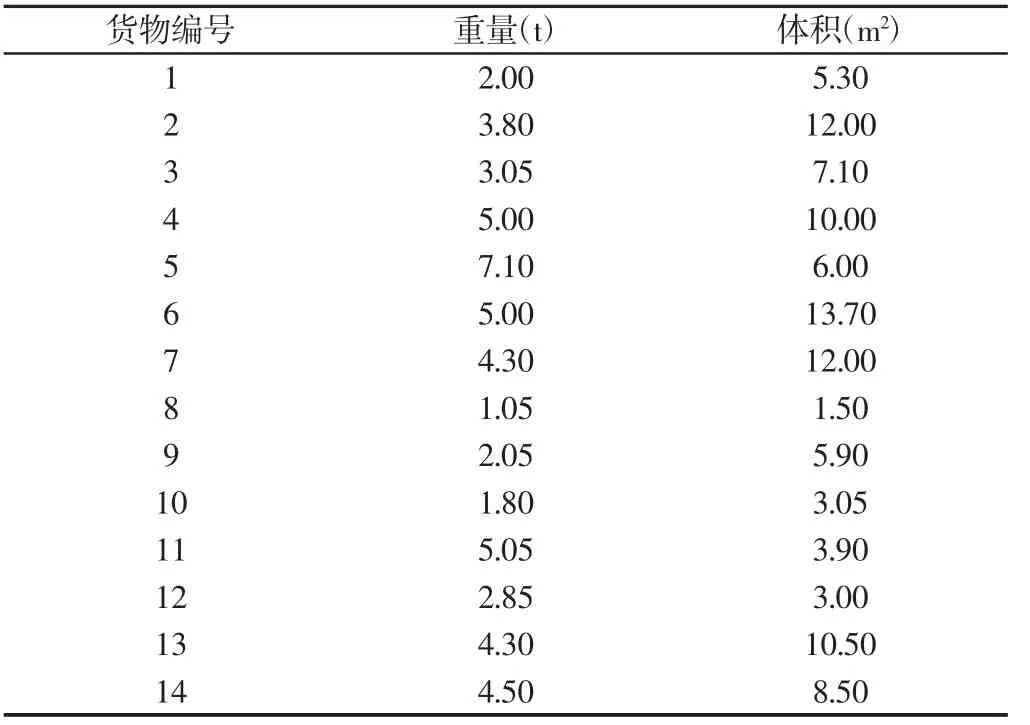
表1 订单配装货物信息表Tab.1 Orders for Freight Loading Information Table

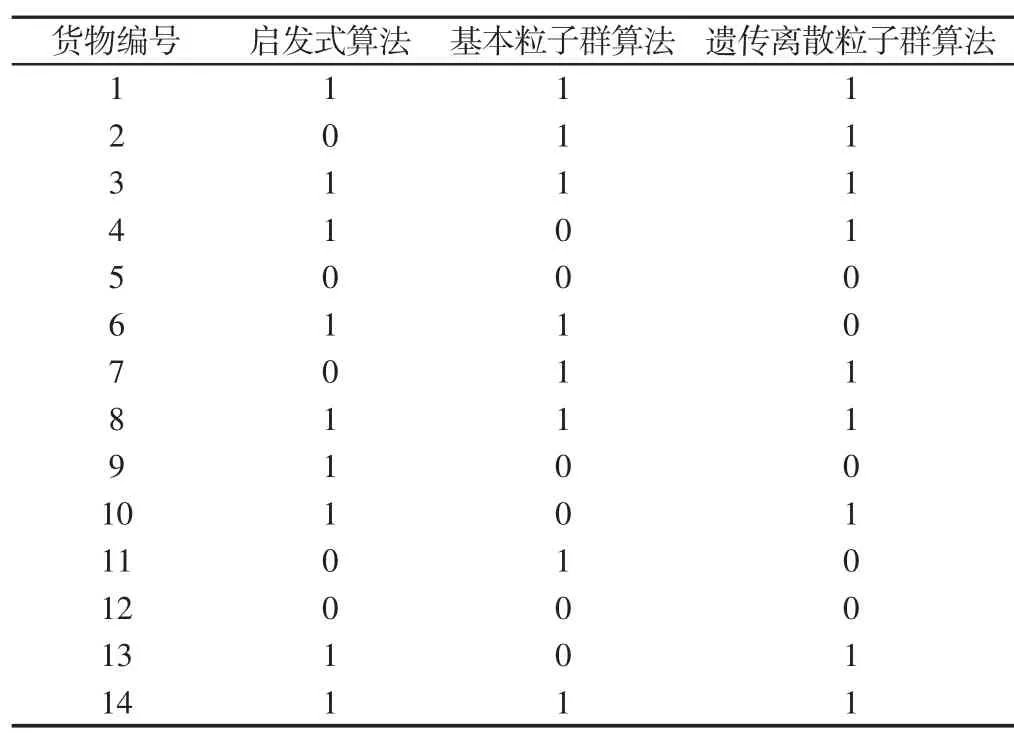
表2 优化配装结果Tab.2 The Optimization Results

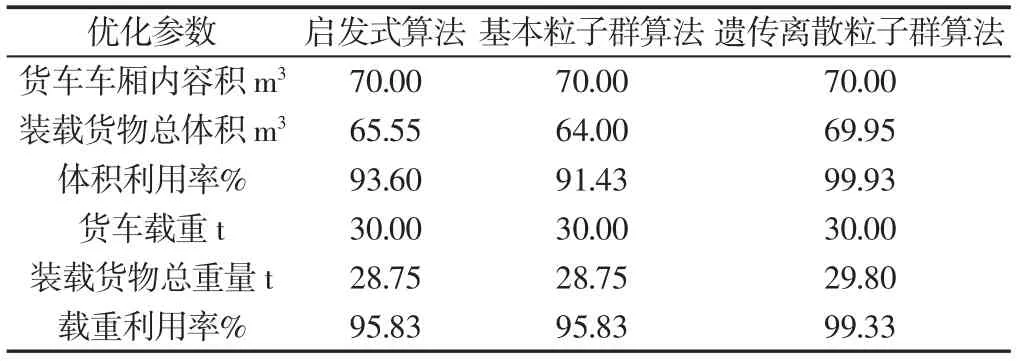
表3 结果对比Tab.3 Comparison Results

采用的遗传离散粒子群算法（GDPSO）求解配装问题最优方案：体积利用率为99.93%，比启发式算法（HA）[10]的体积利用率提高了6.33%，比基本粒子群算法（PSO）的体积利用率提高了8.5%。启发式算法与基本粒子群算法的载重利用率均为95.83%，而遗传离散粒子群算法载重利用率为99.33%，比其他两种方法的载重利用率提高3.5%。遗传离散粒子群算法并没有像传统的算法那样，使载重利用率和体积利用率的求解结果顾此失彼，充分均衡地利用了车辆装载空间。

5 结论

首先根据货物配装问题的特点，建立了同时考虑配装车辆载重和体积的数学模型，采用遗传离散粒子群算法求解货物配装问题，通过算例对比，验证了该方法的有效性，该算法克服了传统算法在载重利用率和体积利用率上顾此失彼，无法同时达到最优的缺点，充分合理地利用了车辆的载重和体积，使车辆的总体利用率达到最大，对企业经营成本的降低，作业效率的改善具有较好指导意义。