三角形级联固态变压器的多直流电压平衡控制
季振东,孙毅超,金 成,王建华,赵剑锋
1. 南京理工大学 自动化学院,江苏 南京 210094;2. 南京师范大学 电气与自动化工程学院,江苏 南京 210042;3. 东南大学 江苏省智能电网技术与装备重点实验室,江苏 南京 210096)
0 引言
固态变压器SST(Solid State Transformer)利用电力电子变换和中高频电磁耦合进行电能传递,在完成传统电力变压器的隔离和电压变换功能的基础上,还可以实现故障隔离、电能质量治理、直流端口及电能管理等功能。它具备解决现代电力系统中许多新问题的潜力,将成为构建智能电网以及未来能源互联网的关键设备之一[1- 4]。
SST在发展过程中形成了很多种类型的拓扑结构,其中三级式(AC/DC-DC/AC)拓扑是目前广泛采用的,该类型虽然增加了电能转换级数和开关器件数量,但由于其输入、输出侧均存在直流环节,提升了其对电能的控制灵活度,拓宽了应用范围[1,3-5]。在中高压大功率领域中,采用三级式结构的级联型SST成为近年来的研究热点,美国北卡罗莱纳州立大学的FREEDM(Future Renewable Electric Energy Delivery and Management)系统[4,11-12]、ABB公司的PETT(Power Electronic Traction Transformer)项目[6]以及美国电科院的IUT(Intelligent Universal Transformer)项目[7]均基于该拓扑结构开展了单相级联SST的研究。而在高压配电网应用中,用三相级联SST有更好的应用前景,其中三角形级联结构能够实现更大容量和更强的不平衡无功补偿能力[8]。
级联SST的拓扑结构中存在多H桥模块串联和多双有源桥DAB(Dual Active Bridge)模块并联的形式。对各H桥模块而言,存在器件参数、损耗以及脉冲延时等差异,连接的电网还有电压不平衡等因素,这就会造成直流侧电压不平衡的问题[9],影响装置的可靠运行;同样在多DAB并联系统中,各模块的损耗、变压器变比以及漏感等会存在偏差,而这些所导致的电流分配不均衡会造成各模块寿命不同以及额定负载下部分模块的过流问题[10]。故而,级联SST在控制中需要解决多直流电压平衡及功率均衡问题。文献[10-15]中的解决思路是将级联H桥系统和多DAB并联系统进行分级独立控制。对于单相级联SST,文献[10-13]在级联H桥部分中加入了相内直流电压平衡控制,而多DAB并联部分采用了均流/均功率控制,这样需要增设若干电流传感器。而文献[14-15]使用了无电流传感器的功率均衡控制,DAB并联系统中的各模块功率调整直接利用前级电压平衡控制的中间量进行修正。文献[16-17]针对三角形级联SST,在级联H桥中注入零序电流以进行相间直流电压平衡控制,而DAB并联系统仍然采用均电流/功率控制。由于现有的无电流传感器功率均衡控制无法进行相间DAB模块功率调节,从而难以扩展到三相系统。另外,当分级独立控制下的级联SST应用于不平衡无功补偿时,三角形级联H桥中的开关器件需要较大的电流裕度[8]。
本文对适用于三角形级联SST的控制策略开展研究。首先,在分析级联SST拓扑和数学模型的基础上提出了一种多直流电压平衡控制方法,并与传统方法进行了比较;然后,利用平均功率模型对传统方法和所提方法下的相内和相间功率特性进行了比较分析;最后,通过仿真和实验对提出方法的有效性和可行性进行了验证。
1 数学模型及控制策略
图1(a)为本文所研究的三角形级联SST的整体结构框图,三相链节在交流侧连接成三角形,而三相链节的直流端口直接并联。图1(b)中的每相链节由多个模块组输入串联、输出并联构成,模块组中H桥模块和DAB模块通过直流端口相连接。图中,iA、iB、iC为各相并网电流;iAB、iBC、iCA为各链节电流。可将三角形级联SST按交流级和直流级来进行划分,交流级为三角形级联H桥变流器,直流级为多DAB输出并联系统。需要注意的是,本文只研究文献中三级式结构的前两级,输出的低压逆变环节研究比较成熟,不在本文的研究范围内。
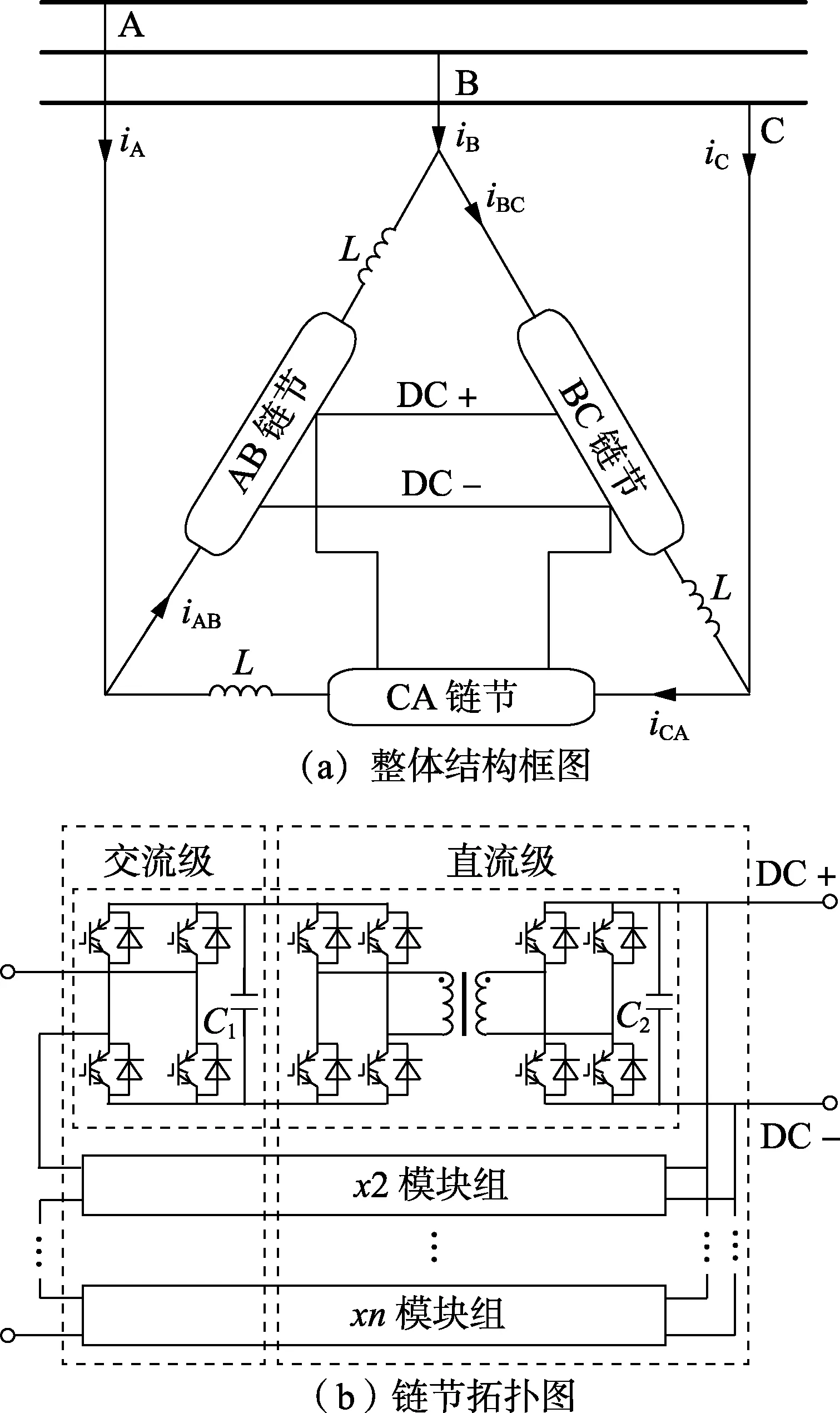
图1 三角形级联SST拓扑结构Fig.1 Topology of cascaded SST with delta configuration
1.1 数学模型
三角形级联SST的交流级和直流级均为多端口系统,庞杂的系统参数造成了数学模型过于复杂,从而不利用控制系统的设计。为了建立简化的系统平均数学模型,做如下假设:
a. 各模块组参数完全一致,交流级的电容值均为C1,直流级输出的电容值均为C2,中频变压器的变比均为Nm、漏抗均为Lm;
b. 交流级的各直流电压均衡,即udc=udcxi(x=AB,BC,CA;i=1,2,…,n);
c. 直流级各DAB模块采用移相控制,且移相角一致,即φ=φxi;
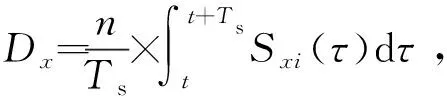
在以上假设条件下,各DAB模块的原、副边电流分别一致,即ip=ipxi且is=isxi。进一步,根据基尔霍夫电压定律和基尔霍夫电流定律,得到级联SST在开关周期内满足:
(1)
(2)
(3)
其中,〈 〉Ts表示开关周期内的平均值;ex和ix分别为各相链节的并网电压和电流;udco为直流级输出电压;R为直流输出端口连接负载的等效阻值。
将式(1)、(2)的abc三相平均模型转换到dq0旋转坐标系下,可以推导出:
(4)
其中,id、iq、iz为三相链节电流在dq0坐标系下的分量;ed、eq、e0为电网线电压在dq0坐标系下的分量;Dd、Dq、D0为三相链节的总占空在dq0坐标系下的分量。
据文献[14],DAB功率PDAB在开关周期内表示为:
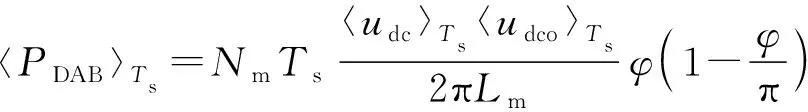
(5)
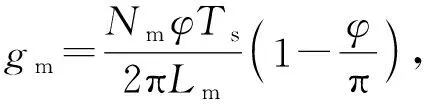
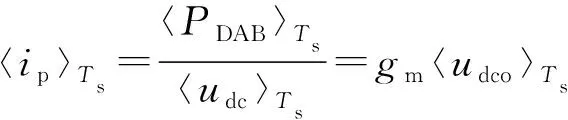
(6)
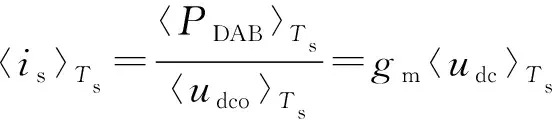
(7)
从而可以根据式(3)、(4)、(6)、(7)得到如附录A中图A1所示的三角形级联SST的简化平均模型。
1.2 多直流电压平衡控制策略
由简化平均模型可知,三角形级联SST的交流级可以等效为三相电压型脉冲宽度调制(PWM)整流器,直流级可以等效为单个DAB。故而,交流级的整体控制可以采用双闭环解耦控制实现并网电流和整体直流电压的控制,直流级可使用移相控制方法以达到输出直流电压的稳定。而对于实现交流级的多直流电压平衡和直流级的电流均衡,传统控制方法是将两级独立开来进行控制,在交流级控制系统中加入相间和相内直流电压平衡控制,同时在直流级加入均功率/电流控制。本文提出的方法将两级综合进行考虑,仅需要在直流级控制中加入电压平衡控制,实现方法如图2所示。
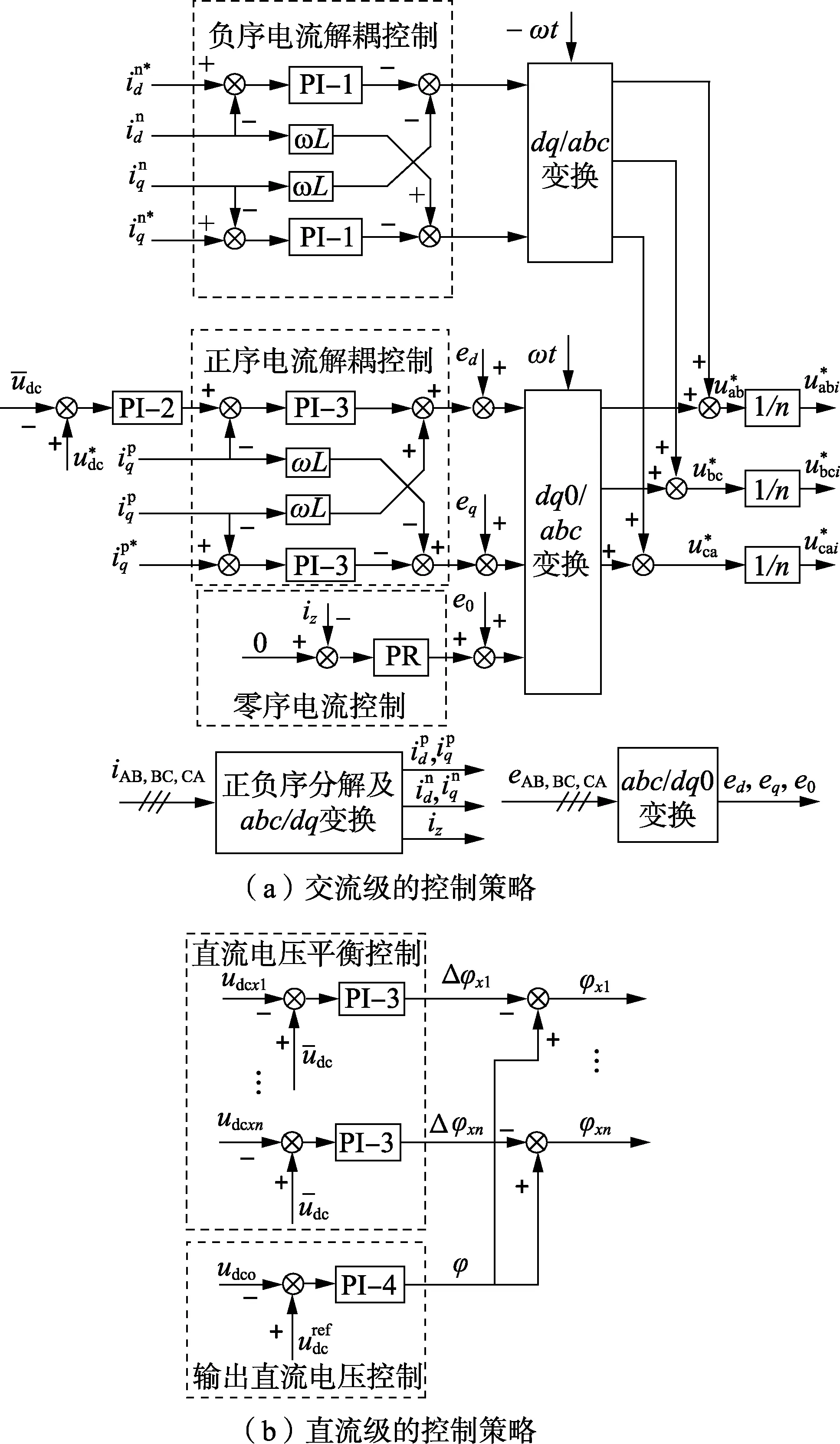
图2 提出的多直流电压平衡控制策略Fig.2 Proposed DC voltages balancing control strategy
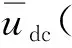
图3为本文所提方法(点划线框部分)与传统方法(虚线框部分)的对比图。可以看出,在交流级系统控制中,所提控制方法取消了相间和相内直流电压平衡控制2个部分,大幅降低了该部分的运算量;而对于直流级系统控制,所提控制方法采用电压平衡控制,在控制复杂度不变的同时,消除了DAB模块的输出电流采样,减少了控制系统的硬件成本。第2节将具体对2种控制方法的功率控制特性进行分析。
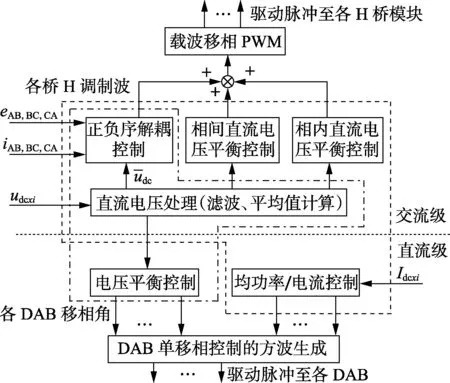
图3 SST的控制策略对比图Fig.3 Comparison diagram of conventional and proposed methods for cascaded SST
2 级联型SST的功率特性分析
2.1 相内功率分析
附录A中图A2为级联SST的单相链节等效示意图。图中,Ex为电网电压有效值;Ix为并网电流有效值;mx1、mx2、…、mxn为各H桥模块的调制比;Udco为输出直流电压平均值;IDCx1、IDCx2、…、IDCxn为各DAB输出的电流均值。各模块组的输入有功功率为:
(8)
其中,θx1、θx2、…、θxn为各模块组中H桥的输出功率因数角。各模块组的输出功率为:
(9)
在理想条件下(各模块组效率一致),采用传统的分级独立控制方法,输出均流/均功率即Pox1=Pox2=…=Poxn,从而各H桥等效负载一致,在相内直流电压平衡控制下其调制波一致,由式(8)可以得到Udcx1=Udcx2=…=Udcxn;而采用提出的多直流电压平衡控制方法亦可以推导出输出均流/均功率,故而理想条件下传统方法与所提方法是等效的。进一步,假设ηx1、ηx2、…、ηxn为各模块组效率。
a. 在传统的分级独立控制下,各模块组输出电流均衡即各模块组的输出功率相等,Pox1=Pox2=…=Poxn,从而可以得到:
Pinx1ηx1=Pinx2ηx2=…=Pinxnηxn
(10)
由于交流级在控制下多直流电压保持平衡,即满足Udcx1=Udcx2=…=Udcxn,代入式(8)可得如下关系:
mx1cosθx1ηx1=mx2cosθx2ηx2=…=mxncosθxnηxn
(11)
从式(11)可以看出,如果各模块工作效率一致,则直流级不会给交流级带来不平衡问题,否则直流级的效率不一致带来的功率不平衡问题需要通过调节各H桥模块输出电压的有功分量来解决。
b. 在提出的多直流电压平衡控制方法下,交流级各H桥调制波完全一致,即mx1=mx2=…=mxn,cosθx1=cosθx2=…=cosθxn且Udcx1=Udcx2=…=Udcxn,故各模块组的输入功率相等,即Pinx1=Pinx2=…=Pinxn,则:
(12)
由于各模块组的输出电压相同,进而可以得到如下关系:
(13)
从式(13)可以得到,当各模块组的工作效率相同时,输出电流保持一致,与并联均流控制达到了一样的控制效果;否则,各模块组输出电流与效率成正比,效率不一致带来的相内功率不均衡问题会通过输出电流体现出来。
2.2 相间功率分析
级联SST具有静止同步补偿器(STATCOM)的功能,需要补偿正序、负序无功电流。而对于传统的分级独立控制,交流级的2种相间平衡控制方法——零序电流注入法和分相控制法是等效的[8],本文选取零序电流注入法来进行分析。将三角形级联SST中的线电压、相电流定义如下:
(14)
(15)
其中,ep为正序电压分量的幅值;Ip、In、Iz分别为正序、负序、零序电流的幅值,θp、θn、θz则分别为对应电流分量的相角值。
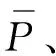
(16)
(17)
(18)
(19)
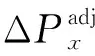
PABηAB=PBCηBC=PCAηCA
(20)
其中,ηAB、ηBC、ηCA为各链节工作效率。而当SST仅用于无功补偿模式时,直流级处于轻载状态,故而DAB的开关器件易工作于硬开关模式。
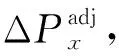
从以上分析可以看出,采用所提方法进行不平衡无功补偿,交流级的三角形级联H桥不需要提供额外的电流裕度(零序电流)来进行相间直流电压平衡控制,同时又充分利用了直流级多DAB并联系统的空闲功率裕量,从而可以避免DAB处于轻载状态,进而有利于满足DAB变换器软开关工作条件[18]。
综上所述,理想条件下传统方法可以取得和提出的多直流电压平衡控制方法一样的效果;但当存在相间功率不平衡因素时,提出的多直流电压平衡控制方法则比传统方法具有更好的效果,特别是在不平衡无功补偿方面。
3 仿真分析
为了验证多直流电压平衡控制方法的有效性和功率特性,通过MATLAB/Simulink对三角形级联SST进行了有功传输和无功补偿下的仿真分析,并和传统的分级独立控制进行了对比,具体参数如附录B中表B1所示。
3.1 有功传输对比仿真
为了验证有功功率传输特性,级联SST直流输出带载2.3 Ω,并通过在各DAB变换器中并联电阻来模拟各模块组不一样的效率(RAB1=1 000 Ω,RAB2=900 Ω,RAB3=1 200 Ω;RBC1=100 Ω,RBC2=80 Ω,RBC3=130 Ω;RCA1=50 Ω,RCA2=60 Ω,RCA3=80 Ω)。
由附录A中图A4(a)可以看出,传统方法在直流级采用均流控制,各链节的DAB模块平均输出电流接近一致,而其输入电流由于不同的效率而产生了不均衡现象。这样导致各H桥模块负载不同,在交流级相间、相内平衡控制的调节下,多模块直流电压保持平衡状态,而各H桥调制波和直流电压纹波则不相同。同时,由于零序电流的注入,级联SST的三相并网电流一直处于平衡状态。图A4(b)为所提方法下的仿真波形,由于交流级只控制直流电压均值,各链节中H桥调制波相同,故而各模块组输入功率相同,体现为图中的各相DAB模块输入平均电流一致。与此同时,各模块组损耗不同导致各相DAB模块输出平均电流不一致,验证了第2节中的效率与功率的关系特性。
3.2 无功补偿对比仿真
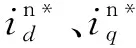
图4为在传统的分级独立控制方法下的负序电流补偿仿真波形,交流级通过注入零序电流来调节相间功率并保持直流电压平衡。从图中可以看出,并网线电流跟随指令值变化,而由于注入零序电流不断变化导致各链节的相电流大幅波动,符合文献[8]中所描述的相电流变化规律且最大处为2倍的负序电流。
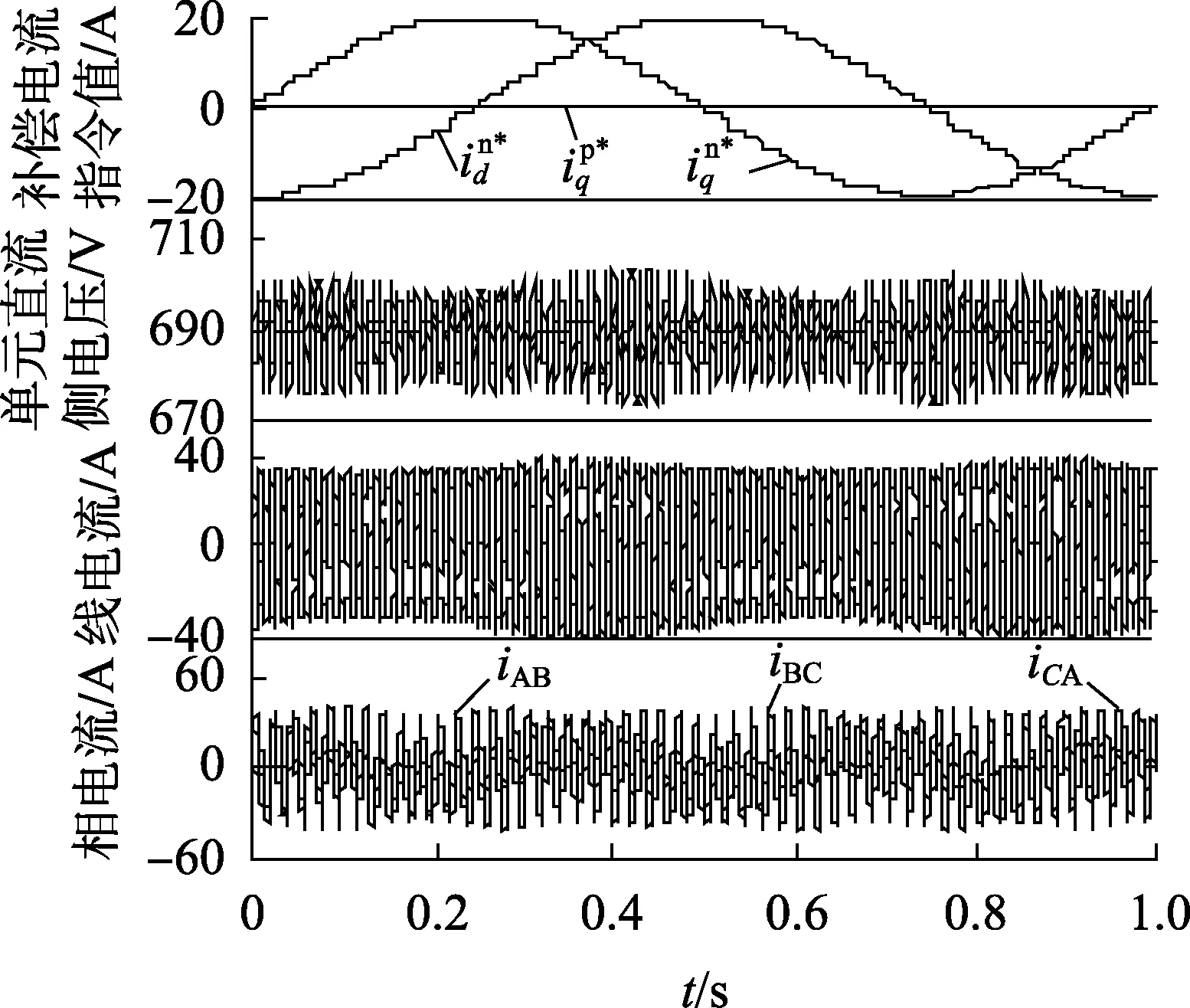
图4 传统控制方法下的负序电流变化仿真图Fig.4 Waveforms during change of negative-sequence currents with traditional control method
图5为在所提方法下的负序电流补偿仿真波形,图中并网线电流和传统控制方法下的线电流基本相同,而各链节的相电流与线电流变化规律一致,并未出现大幅度的波动,且最大相电流波动远小于传统控制下的波动,验证了所提方法可大幅减少交流级器件的电流裕度。同时,相间的功率不平衡因素引入了直流级,直流级各链节DAB模块输入和输出电流均呈现出周期性波动以进行相间有功交换。仿真表明,采用所提控制方法的三角形级联SST具备更好的不平衡无功补偿能力。
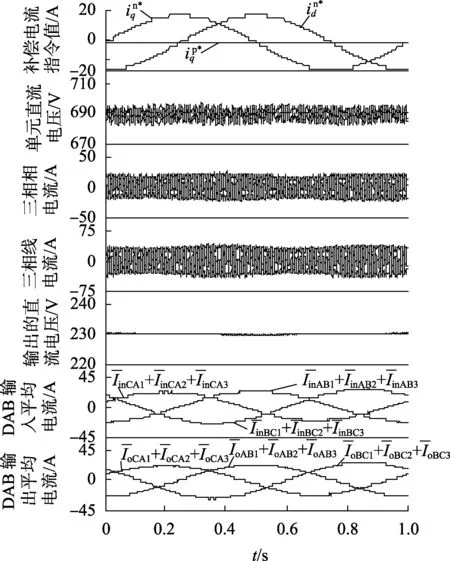
图5 所提控制方法下的负序电流变化仿真波形Fig.5 Waveforms during change of negative-sequence currents with proposed control method
4 试验验证
进一步,通过试验平台对所提出的多直流电压平衡控制方法进行验证,具体试验参数如附录B中表B2所示。
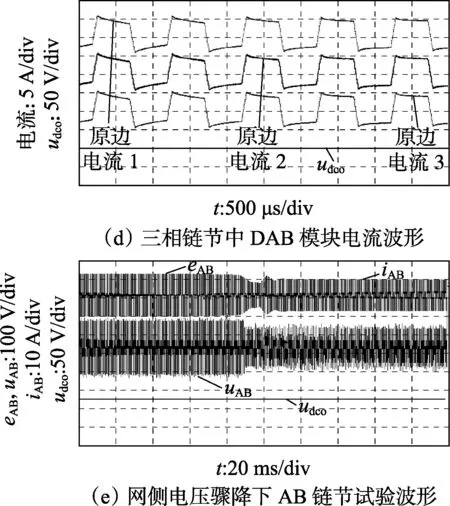
图6 有功传输下三角形级联SST的试验波形Fig.6 Experimental waveforms of cascaded SST with delta configuration under active power transmission
图6为有功传输条件下的稳态试验波形。图6(a) 为电网相电压eA、并网线电流iA和iB、直流级输出电压udco的波形;图6(b)为AB链节的电网线电压eAB和相电流iAB、AB链节输出的七电平电压uAB的波形,也说明了相内三单元的直流电压的平衡;图6(c)为其中一个DAB模块的中频变压器原、副边的输入电压及原边的电流波形,副边电压滞后于原边,电能由原边传递至副边;图6(d)为其中3个DAB模块的原边电流及输出直流端口的电压波形,3个DAB模块电流平衡且有稳定的输出电压;图6(e)为网侧电压骤降下eAB、iAB、uAB、udco的波形,各链节输出电压跟随降低以调整并网电流,输出直流电压在突变过程中保持恒定。
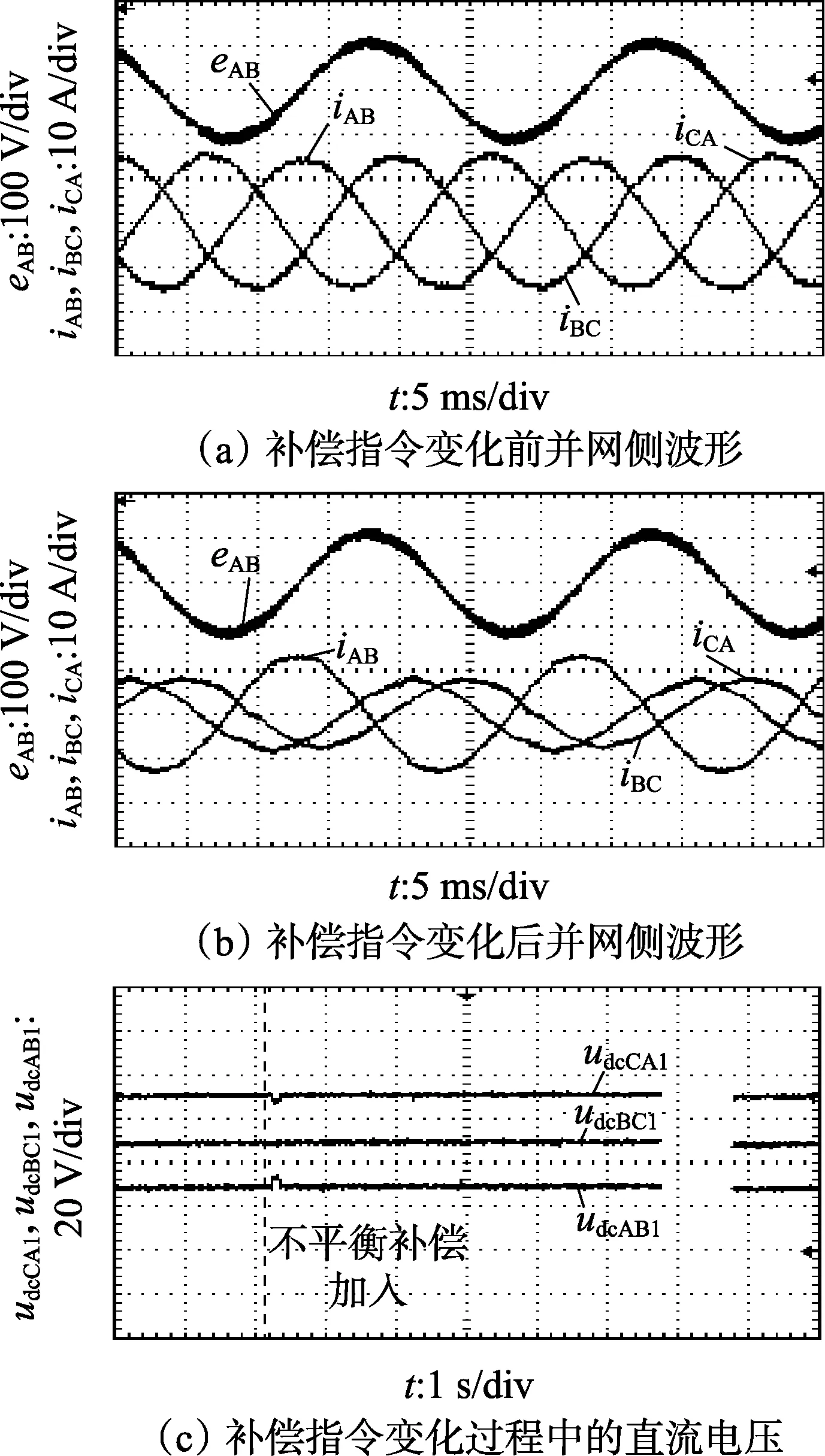
图7 无功补偿下的三角形级联SST的试验波形Fig.7 Experimental waveforms of cascaded SST with delta configuration under reactive power compensation
图7为三角形级联SST用于无功补偿的动态试验波形。图7(a)为补偿无功突变前仅含有正序补偿指令值的工况下并网侧波形;图7(b)为突变后不平衡无功补偿的工况下并网侧波形;图7(c)为动态变化过程中的各相链节直流电压波形。可以看出,在无功补偿值突变过程中,各相链节的直流电压经过微小波动后保持稳定,达到了预期的不平衡无功补偿效果。
从以上试验可以看出,在传输有功功率时,SST样机的三相并网电流平衡、各DAB模块达到了均流效果且维持了输出直流端口电压的稳定;无功补偿突变情况下,各直流电压保持了平衡状态。各试验波形均符合控制目标,从而验证了提出的多直流电压平衡控制方法的可行性和有效性。
5 结论
本文针对三角形级联SST提出了一种新型的多直流电压平衡控制方法,该方法对交流级实行平均直流电压控制,同时在直流级采用直流电压平衡控制。在实现多直流电压平衡和功率均衡的同时,消除了多DAB并联系统中的电流传感器,降低了控制系统复杂度,并给装置带来了更好的不平衡无功补偿能力。通过仿真和试验验证了本文所提控制方法的可行性和有效性,结果表明所提方法有较好的稳态和暂态性能,对于其未来在新能源发电并网、机车牵引、能源互联网等场合的应用具有重要价值。
附录见本刊网络版(http:∥www.epae.cn)。

