基于试验设计的电动汽车充换电站接入电网的降损研究

刘新天,尤俊杰，何 耀，郑昕昕，曾国建

合肥工业大学 智能制造研究院，安徽 合肥 230009)

0 引言

电动汽车的车载动力电池是一种分布式的储能单元,它既可以通过充换电站从电网获取电能提供电动汽车行驶的动力,也可作为分布式电源DG(Distributed Generation)通过充换电站将电池储存的能量回馈给电力系统,这种电动汽车与电网之间能量双向互动的关系被称为车网互联V2G(Vehicle to Grid)模式[1-2]。 无论动力电池处于充电还是放电状态，充换电站与电网交换的功率都存在一定的随机性和间歇性，当其大规模投入使用时，将会对配电网的潮流分布产生影响，进而引起网络损耗的变化[3]。如何合理调控充换电站的工作行为，降低配电网损耗，确保电网安全经济运行，是一个值得关注和研究的重要课题。

目前针对电动汽车充换电站入网的研究主要集中在充换电站的选址定容规划[4-7]、充换电站与风光等新能源电站的联合调度[8-12]方面，而利用充换电站V2G模式来降低网损的研究很少。国内外关于DG配置及调度的优化方法，大体可划分为理论最优研究和启发性方法2类。理论最优研究主要包括一些经典的数学方法，如拉格朗日法[13]、割平面法、原-对偶内点法[4]等；启发性方法包括当前热门的智能优化算法，如遗传算法[6,8,12]、粒子群优化算法[7,9]、蚁群算法、模拟退火法等。经典数学法用数学来优化模型，在理论上往往可以保证解的最优性，但实际计算量大；智能优化算法通过模拟某一自然现象或过程而建立，具有高度并行、自适应的优点，但往往存在自身的缺点，需要进行改进。本文的研究目的是针对未来规模化充换电站的降损设计，其特征是小区域、大范围和控制轻便化，相对于最优算法，本文倾向于采用启发性方法。这类启发性方法往往无需考虑收敛问题，使复杂问题简化，从而减小计算量，缩短计算时间，虽然其也许不能保证得到最优解，但依旧具有极大程度的优化。文献[14]将配电网看作一个不规则的物体、节点负荷看作该物体的一处质量、DG的供电范围看作一个不规则形状的负荷块，DG安装在负荷块的质心时，配电网有功损耗最小。文献[15]提出一种2/3准则，用来确定DG在配电网的最优位置，使得馈线有功网损最小。文献[16]采用混合可再生能源系统建模软件HOMER进行研究，对杭州市风、光、水能源并网型微网进行优化，HOMER采用穷举法进行计算分析。文献[17]针对梯级水电站的优化调度，提出了采用正交试验设计和离散微分动态规划(DDDP)相结合的正交离散微分动态规划方法。然而上述文献没有针对性地研究充换电站对所属区域配电系统的电气接入点和其接入功率。除此之外，充换电站兼具电源和负荷的特性，需要考虑这一条件进行深入分析。针对这些问题，本文采用试验设计DOE(Design Of Experiment)方法，利用部分析因设计与中心复合设计CCD(Central Composite Design)的思路开展研究。DOE是一种起源于统计学原理的安排试验和分析试验数据的数理统计方法。通过对试验的合理安排，以较小的试验规模和较少的试验次数，得到理想的试验结果和得出科学的结论，在航天工业、一般生产制造业和医学领域都得到了一定的应用[18]。

本文首先分析了单个充换电站接入配电系统中对系统有功损耗的影响。由于配电系统支路、节点数目众多，多个充换电站接入配电系统不同电气接入点后对配电网有功损耗的影响情况较为复杂，因此采用DOE方法中的Plackett-Burman设计进行试验安排和数据分析，并以IEEE 33节点配电系统为例进行说明和验证。然后针对多个未知运行状态的充换电站接入配电系统某些固定电气节点的情况，利用CCD进行响应曲面设计RSM(Response Surface Methodology)，拟合出充换电站接入配电网模型不同电气节点时，充换电站工作情况与配电网有功损耗之间的关系。最后以降低损耗为目标，对充换电站接入配电系统的最佳工作功率进行组合优化。

1 充换电站接入配电网的理想模型分析

V2G模式的电动汽车充换电站接入配电网时，会导致电力系统潮流发生改变，原本单向流动的潮流可能会变成双向流动，配电网潮流的改变会造成网络损耗的变化。图1给出了配电网支路i-j的示意图，以此为基础来简明表示充换电站接入配电网的模型。配电网节点j接有负荷，为星形连接且三相平衡，该负荷以一定的功率因数从系统中吸收有功功率Pm和无功功率Qm。

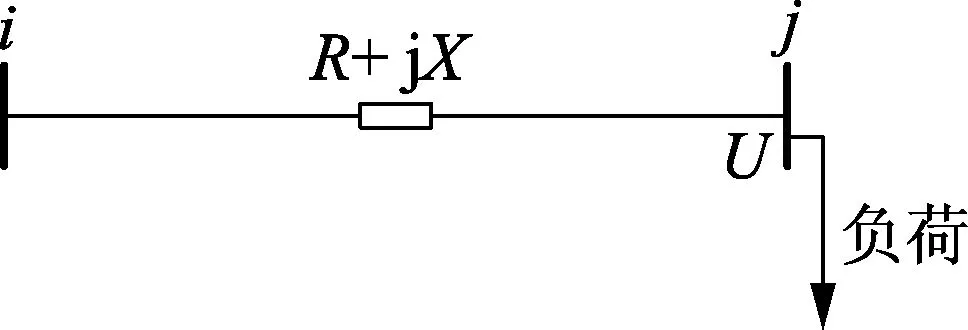
图1 配电网支路i-j的示意图Fig.1 Schematic diagram of branch i-j in distribution network

此时，系统负荷为：

S0=Pm+jQm

(1)

流向负荷的单相电流为：

(2)

系统网损为：

(3)

其中，r为线路的单位长度电阻；L为线路长度。

电动汽车充换电站在某一时刻的总负荷可认为是站中所有充放电桩工作功率的叠加。当充换电站接入某节点后，节点的负荷发生改变，需要再次进行分析。图2给出了充换电站接入节点j后的情况。此时系统负荷为：

S=(Pm+Pc)+j(Qm+Qc)

(4)

其中，Pc、Qc分别为电动汽车充换电站注入节点的有功功率、无功功率。

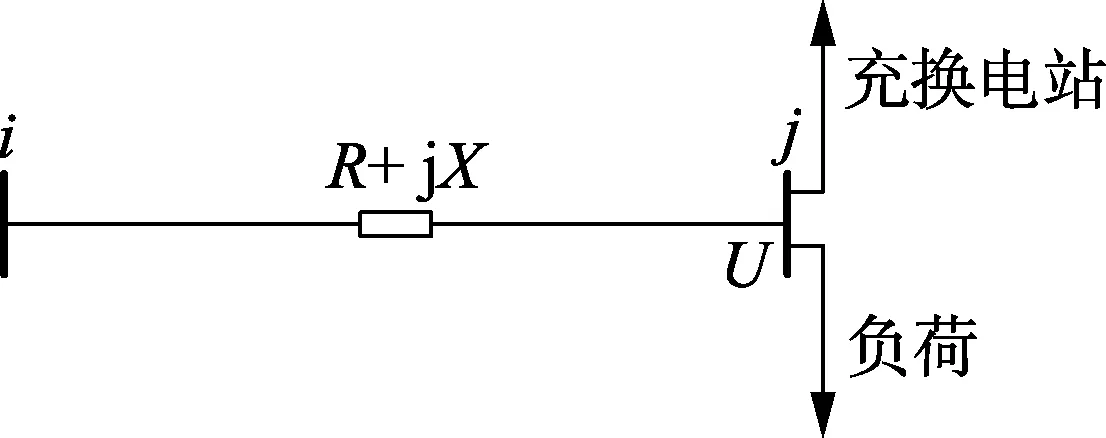
图2 配电网支路i-j的示意图Fig.2 Schematic diagram of branch i-j in distribution network

流向负荷的单相电流为：

(5)

系统网损为：

(6)

比较2种情况下的系统损耗，可以得到接入充换电站后的网损变化量ΔP为：

(7)

由上式可知，ΔP数值的正负体现了网络损耗是变大还是变小，这取决于Pc、Qc的取值，而Pc、Qc的取值反映的就是充换电站的工作状态。如果在负荷侧引入充换电站，当充换电站以一定的功率向电网反送电能时，就可以在一定程度上减少系统支路上的电流，从而减小网络损耗。

2 单个充换电站对配电网网损的影响

采用DOE方法用于安排试验和分析试验结果，首先要明确如何进行试验。考虑到实际配电网的特点，本文采用适用于配电网潮流分析的牛顿拉夫逊法来进行潮流计算[19]，针对给定的算例场景和初始条件，计算充换电站接入配电系统不同电气节点时的潮流结果。

本文针对具有代表性的IEEE 33节点配电系统展开分析，配电系统拓扑结构如图3所示，文献[20]给出了其支路参数和母线负荷数据，取基准电压和基准功率分别为12.66 kV和10 MV·A。

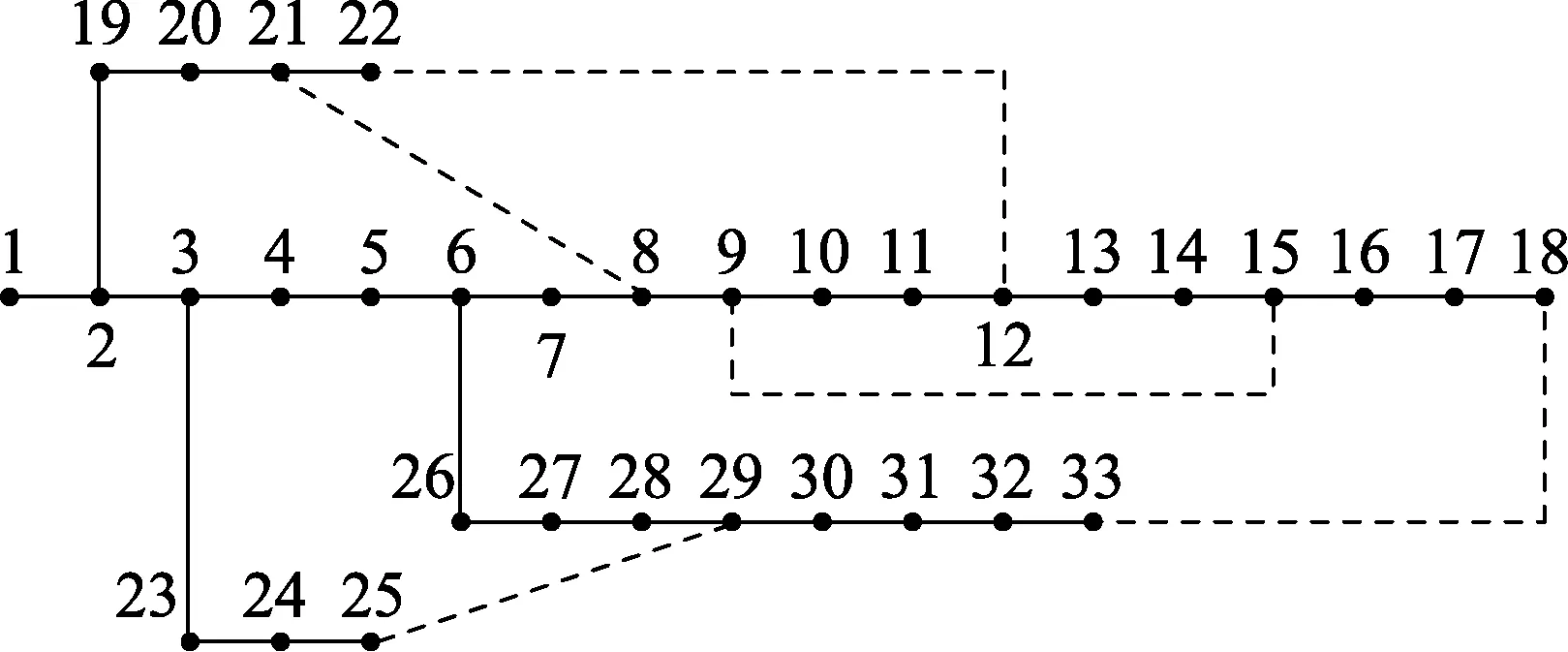
图3 IEEE 33节点配电网系统拓扑结构Fig.3 Topological structure of IEEE 33-bus system

为直观反映规律，只对充换电站接入同一馈线上的不同电气节点进行比较，此处选择节点1—18，其中节点1为平衡节点。假设充换电站与电网和电动汽车之间只有有功功率的交换，功率因数为1。当充换电站接入功率为正时，表示充换电站向电动汽车提供电能，即相当于接入配电网的负荷；当充换电站接入功率为负时，表示充换电站向电网反送电能，相当于接入配电网的DG。当系统中未接入充换电站时，系统的有功损耗为0.36 MW。充换电站分别作为负荷和DG以0.24 MW、0.5 MW和1 MW的容量接入负荷节点1、2、…、18，其计算得到的有功损耗结果如图4和图5所示。

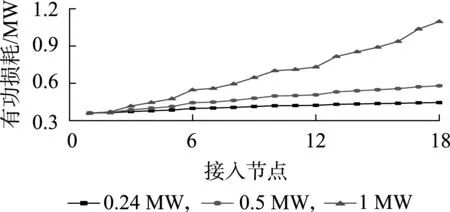
图4 充换电站作为负荷接入不同位置对有功网损的影响Fig.4 Influence of charging and swapping station as load access to different positions on active power loss

图5 充换电站作为DG接入不同位置对有功网损的影响Fig.5 Influence of charging and swapping station as DG access to different positions on active power loss

由图4可知，充换电站作为负荷接入配电网时，离电源的电气距离越远，接入容量越大，系统网损越大。由图5可知，充换电站作为DG接入配电网时，接入容量不同，产生最小网损所对应的接入节点位置也不同。当接入小容量的充换电站时，离电源越远，网损降低得越多；而随着容量逐渐变大，网络损耗曲线也逐渐变为U形，最小网损对应的位置并非出现在最末端。可见，电动汽车充换电站因其工作状态不同，在某些特定情况下可以起一定降损效果，有利于配电网经济运行。

3 多个充换电站接入电网的网损分析

3.1 多个充换电站接入电网模型

利用DOE方法研究运行状态未知的多个充换电站接入配电网的降损问题，关键是可以把节点众多的配电网看作是一个黑匣子。如图6所示，将运行状态未知的充换电站接入配电网，将除与主网连接外的其余N-1个节点等效成不同水平的N-1个因子，从而去影响网损这个变量。

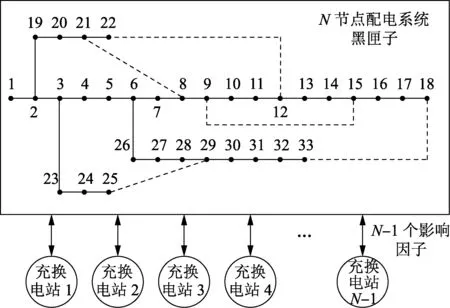
图6 多个充换电站接入配电网的黑匣子示意Fig.6 Black box illustration of charging and swapping stations access to distribution network

3.2 因素分析及因子水平选择

由于选用IEEE 33节点配电网模型，该系统有33个节点，除了平衡节点1外，充换电站作为负荷或DG可能接入该模型的其余每个节点中，故本试验的因子个数为32个。

考虑到环保和经济性的要求，充换电站需要运行在额定工况附近，故本文对其采用恒功率模型。本文取充换电站功率因数为1，即充换电站与电网之间只有有功功率的交换，因此Qc=0。当Pc=0时表示充换电站处于不工作状态未接入配电系统，当Pc>0时表示充换电站给电动汽车充电，当Pc<0时表示充换电站向电网放电。以充换电站额定功率为0.24 MW 为例，每个因子皆有2个水平，高水平(+1)表示充换电站以0.24 MW的功率投入运行给电动汽车充电，低水平(-1)表示充换电站以0.24 MW的功率向电网放电。若规定充换电站从电网获得能量给电动汽车充电的工作功率为正，则充换电站工作功率的取值在区间[-0.24，0.24]内波动。本试验的响应变量为配电网系统的有功功率损耗。综上所述，这是一个32因子2水平的试验。

3.3 网损-功率影响系数分析

为了研究黑匣子模型，需研究充换电站接入各电气节点的工作功率对系统有功网损的影响程度，这相当于电力系统中节点接入的有功功率对网损的灵敏度分析。采用的方法通常是将有功功率的变化视为正常运行时的一种扰动，对系统网损公式进行求偏导，获得的系数即为灵敏度。系统网损公式一般通过对电网结构分析推导获取，本文则是通过DOE方法进行试验拟合回归方程获得。

由于因子数目较多，若对这些因子进行全因子试验，那么试验次数将急剧增加。然而在回归方程中，除了常数、主效应及二阶交互效应项外，三阶及更高阶项实际上已无具体的物理意义[21]。因此本文采用部分析因设计进行研究，其中Plackett-Burman设计是一类部分析因设计，它允许在合理的试验次数下研究许多因子。研究步骤如下。

a. 利用minitab软件进行Plackett-Burman设计，可得各节点应该接入高水平(+1)、低水平(-1)的试验计划。试验计划包括多组试验方案，这些方案保证了正交性，以确保考虑到每个因子的影响效应。

b. 根据Plackett-Burman设计试验方案，代入实际数据后进行试验，即利用牛顿拉夫逊法进行潮流计算，得到每种方案下有功网损P的数据集合{Si}。

c. 分析数据集合{Si}，拟合出各节点接入功率对系统有功网损P的回归方程。

d. 对有功网损P的回归方程求各节点接入功率的偏导，获取N-1个系数。这些系数表征了各节点的影响程度，可用于进一步分析。

以额定功率为0.24 MW的充换电站接入IEEE 33节点配电系统为例进行上述研究，获得的各节点系数如图7所示。

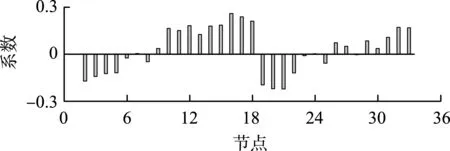
图7 网损-功率系数Fig.7 Coefficient of power loss and power

由图7可知，针对额定功率为0.24 MW的充换电站接入IEEE 33节点配电系统，各节点系数体现出了一些规律。各节点系数有正有负，说明各节点接入工作功率对系统网损的影响不同。节点7、9—18、24、26、27、29、30 —33的系数为正，记作正系数组{S+}，说明这些节点适合在充换电站作为DG时参与调度。节点2— 6、8、19—23、25、28的系数为负，记作负系数组{S-}，说明这些节点适合在充换电站作为负荷时参与调度。适合充换电站作为DG调度的电气节点往往分布在配电系统馈线末端，有利于电量被支线负荷消纳，减少线路上的电能传输，降低网损；而适合充换电站作为负荷调度的电气节点往往靠近电源点，电气距离较小。

正系数组{S+}和负系数组{S-}组内最大值与最小值之间的差值较大，而那些绝对值较大的节点表示影响幅度较大。当接入充换电站个数较小，主效应显著而交互效应较弱时，往往是优先考虑接入点。为了进一步论证，通过3.4节进行深入研究。

3.4 分析典型节点影响

根据图7反映的系数的正负性和绝对值从大到小进行分组和排序，{S+}中的排序结果为16、17、18、15、12、14、32、33、10、11、13、31、29、26、27、9、30、7、24，{S-}中的排序结果为21、20、19、2、3、4、22、5、25、8、6、23、28。

JGJ 3—2010《高层建筑混凝土结构技术规程》规定了扭转周期比T t/T1的限值，其目的是限制T t不要过大，达到适当控制扭转角不要过大效果，即控制结构的扭转刚度不要过弱。但在实际工程中通过调整控制周期比限制可能出现几种情况：（1）通过增大T1来满足扭转周期比，这样做实际并未提高结构的扭转刚度降低结构的T t，而是减弱了结构在平动方向的刚度；（2）同时增大T t与T1来满足扭转周期比限值，与控制目标并不一致；（3）第一平动周期不变，通过减小第一扭转周期来满足周期比的限值，这样与控制结构的扭转刚度不能太小的目标一致。

为了使结果更好地体现差异性，分别取各端情况作为典型节点进行试验分析，则存在4种情况：正系数绝对值较大、正系数绝对值较小、负系数绝对值较大、负系数绝对值较小。根据从大到小或从小到大的原则依次取5个节点作为研究对象，则分组情况如下。S1：正系数绝对值较大，节点16、17、18、15、12。S2：正系数绝对值较小，节点27、9、30、7、24。S3：负系数绝对值较大，节点21、20、19、2、3。S4：负系数绝对值较小，节点25、8、6、23、28。

针对每组的节点，依次选取n(n=2,3,4,5)个节点接入充换电站，利用潮流计算得到每种情况的系统有功网损值，然后求取各组均值μ1—μ4和方差σ1—σ4。假定充换电站全额工作，在峰时作为DG参与调度，在谷时作为负荷参与调度，计算得到的网损均值和方差结果如表1、2所示。

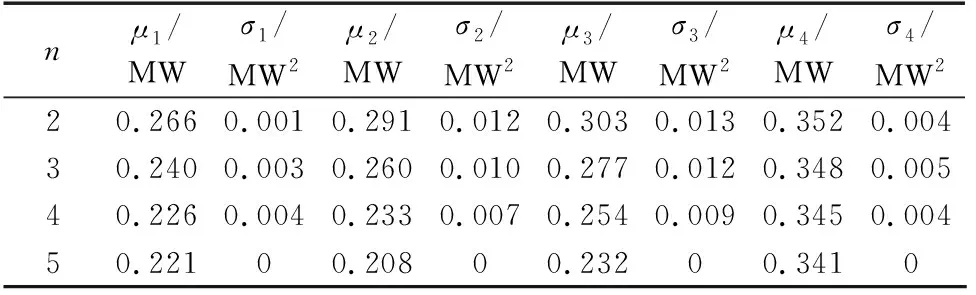
表1 充换电站作为DG时的网损Table 1 Power losses when charging and swapping stations are accessed as DG

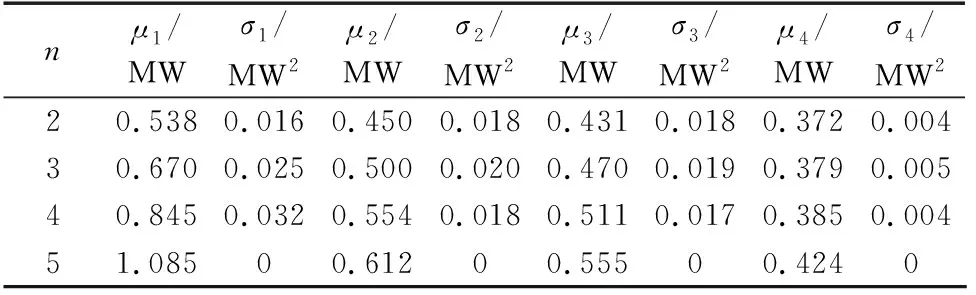
表2 充换电站作为负荷调度时的网损Table 2 Power losses when charging and swapping stations are accessed as load

由表1可知，当充换电站作为DG时，系统网损比未接入时低。随着接入数量n的增加，网损下降，但下降幅度逐渐变缓。若继续增加接入数量，可能会由于接入数量过多造成部分支路潮流逆向，使网损减小幅度变少，甚至会造成系统网损增加。S1、S2、S3、S4的网损均值逐渐增加，可见在S1处充换电站适合作为DG调度。由表2可知，当充换电站作为负荷时，系统网损比未接入时高。随着接入数量n的增加，网损增加，且在S4处网损相对最小。S1、S2、S3、S4的网损均值逐渐降低，可见在S4处充换电站适合作为负荷调度。

4 响应曲面设计估算网损及优化

本文针对多个未知运行状态的充换电站接入配电系统某些固定电气节点的情况，特别是当固定节点数目较少时，提出一种利用响应曲面设计进行配电网有功损耗快速估算的方法，建立了网损回归模型，对接入功率进行组合优化。

4.1 响应曲面设计估算网损

利用响应曲面设计，建立充换电站接入固定节点的网损回归模型，步骤如下。

a. 针对确定的固定节点，利用minitab软件进行CCD，获得CCD试验方案。CCD是一种响应曲面设计，可以拟合得到一个含二次项的回归方程。其一般模型为(以2个自变量为例)：

(8)

其中，x1、x2为自变量，即因子；y为响应变量；b0为常量；b1、b2为线性系数；b11、b22为平方项系数；b12为交互作用系数。

b. 根据CCD试验方案代入实际数据后进行试验，即利用牛顿-拉夫逊法进行潮流计算，得到每种方案下有功网损P的数据集合{Ci}。

c. 对数据集合{Ci}进行拟合，可得有功网损P回归方程的各项系数，剔除不显著作用项后再次拟合，可得到准确的回归方程。该方程函数模型能准确表达出各固定节点接入不同工作功率充换电站时，配电网有功网损P的大小。

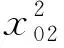
P=b0+b22x22+b21x21+b02x02+b31x31+

b2221x22x21+b2202x22x02+b2231x22x31+

b2102x21x02+b2131x21x31+b0231x02x31+ε

(9)

其中，x22、x21、x02、x31分别为节点22、21、2、31处充换电站的接入功率；b0为常量；b22、b21、b02、b31为线性系数；b2222、b2121、b0202、b3131为平方项系数；b2221、b2202、b2231、b2102、b2131、b0231为交互作用系数。

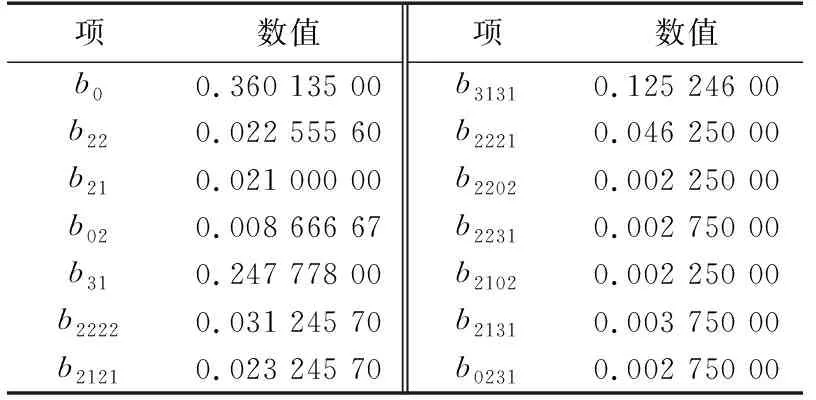
表3 系数估计结果Table 3 Estimated results of coefficients

根据上述拟合的回归方程，将任意两节点置0，即可绘制出其余两节点接入功率对有功网损P的三维响应曲面图，如图8所示,可得有功网损P与其余两节点工作功率大小的变化关系。

4.2 网损模型优化及验证

针对运行状态未知的充换电站接入配电系统某些固定节点，且固定节点数目较少，利用4.1节所提的方法获得网损回归模型，其能够反映各固定节点接入的功率是如何影响系统有功网损P，通过设置合适的自变量，可以使系统有功网损P达到最佳值。

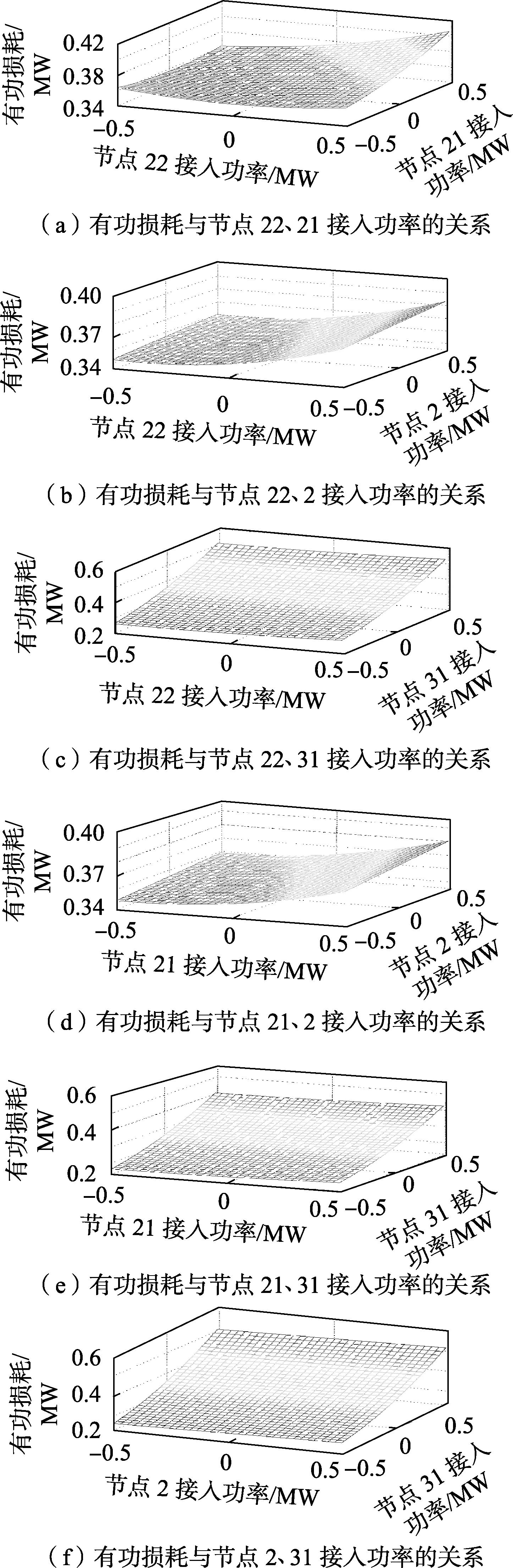
图8 有功损耗与固定节点接入充换电站功率的关系Fig.8 Relationship between active power loss and charging and swapping station power at fixed nodes

利用4.1节中所得的网损回归模型，以网络损耗P最小为目标，采用minitab软件自带的响应优化器进行优化，可直接获得最优解，从而得到各节点应接入的工作功率的优化组合，达到降低网络损耗的目标。响应优化器优化结果如附录中图A1所示。图A1上端列出了各因子变量的名称、取值范围及最优设置，上图为合意值d的取值情况，下图为有功网损P的最优化结果。将采用本文DOE方法获得的系统有功网损值记为PDOE，将在MATLAB中进行潮流计算得到的系统网损值记为PMatlab。可见若在节点22、21、2、31接入额定功率为0.5 MW的充换电站，那么当充换电站接入节点22的工作功率为-0.126 3 MW，接入节点21的工作功率为-0.257 6 MW，接入节点2和节点31的工作功率均为-0.5 MW(记为方案1)时，系统网损最小，此时PDOE达到最小值为0.260 3 MW，在MATLAB中进行潮流计算得到PMatlab为0.261 MW，两者结果基本一致，且方案1比未接入充换电站时的系统网损降低了27.50%。

为说明方案1的优化性，在节点22、21、2、31调整充换电站接入功率，得到不同方案(方案2、3为随机选取)下的配电网网损见表4。可见，各方案PDOE与PMatlab的误差较小，说明了响应曲面法拟合回归模型的准确性；方案2比方案1、方案3的网损大，说明并非所有节点均作为DG就一定会最大限度减小系统网损；方案3表明了充换电站同时在不同节点处作为负荷或DG参与调度也能使系统降损的可能。

表4 不同方案下的配电网网损Table 4 Power losses of distribution network under different cases

5 结论

为更好地利用充换电站以V2G模式接入电网的优势，发挥其降损作用。本文基于IEEE 33节点辐射状配电网模型，对充换电站接入配电网不同位置所产生的网损进行了理论与定量分析。通过DOE方法对固定节点进行响应曲面设计，拟合有功网损的回归方程模型，进而得到有功损耗优化组合。得到的结论如下。

a. 由于充换电站接入位置、工作容量和工作方式的不同，接入配电系统会对网络损耗产生不同程度的影响。针对单个充换电站，其作为负荷调度时，离电源电气距离越远网损越大;作为DG调度时，系统损耗会因为其工作容量的增大，随电气距离的变大逐渐呈U形关系。

b. 针对多个充换电站接入配电系统的情况，由Plackett-Burman设计可以得到各节点接入功率对系统网损的影响系数。进一步研究表明，峰荷期应优先考虑在正系数绝对值较大处的充换电站作为DG调度，谷荷期则应优先考虑在负系数绝对值较大处的充换电站作为负荷调度，以促进配网的经济运行。

c. 针对运行状态未知的充换电站接入配电系统某些固定节点，可利用响应曲面设计方法进行网损回归模型的拟合与优化，结果表明在固定节点合理配置充换电站的接入功率能有效降低配电网网损。

本文方法适用于低压配电网中的电动汽车充换电站在某个台区或某条馈线上的设计，此时换电站之间的关联性比较小。随着配电系统规模变大，本文方法也会变得复杂。结合文献[22]提到的电压分区控制方式的运用背景，当配电网系统规模较大时，可以将配电网分成若干个子区域，这些区域具有内部节点强耦合、不同区域之间弱耦合的特征，分区后的配电网子区域节点个数较少，此时也适用本文方法。