二维带尖点区域上Boussinesq方程组在有限时间爆破的局部光滑解
康 静,邓大文
(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)
Boussinesq方程组描述了不可压流体在有热对流时的流动情况,模拟大气、洋流等实际现象[1-3]。二维无粘性无热传导的Boussinesq方程组的全局正则性是个开问题,即还不清楚局部光滑解是否一定可以延拓为全局光滑解。R2和二维光滑区域上不可压Euler方程组具有全局正则性[4-6],Kiselev和Zlatos[7]在一个有尖点的区域上,对该方程组构造了一类在有限时间爆破的局部光滑解。对无黏性无热传导的Boussinesq方程组,在上述3种区域上的全局正则性都是开问题,本文用Kiselev和Zlatos的方法,在他们使用的有尖点区域上,构造一类在有限时间内爆破的局部光滑解。
1 预备知识
我们先回忆一般二维有界光滑区域Ω上的Boussinesq方程组
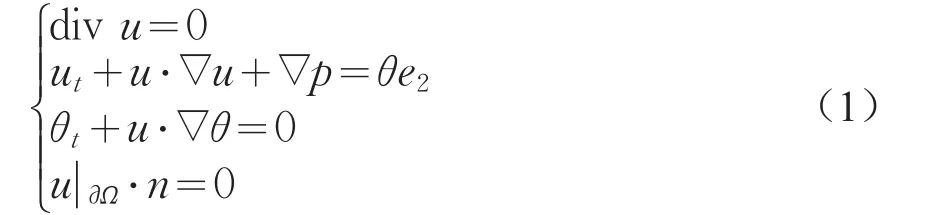
其中 u=(u1(x,t),u2(x,t))是速度场,θ=θ(x,t)∈R是温度场,p=p(x,t)∈R是压力场,x=(x1,x2)∈Ω,t>0,e2=(0,1),n是∂Ω的单位外法向量,u在∂Ω上满足u·n=0。本文约定,(1)i指式(1)中的第i条方程,i=1,2,3。可以把式(1)写成涡量-流函数形式,令ω=为涡量,又由div u=0,知存在流函数 ψ:Ω→R ,使 u=∇⊥ψ ,其中 ∇⊥:=(-∂x2,∂x1)。由式 (1)4,可知ψ|∂Ω为常数,不妨设为0。所以式(1)可写成

可参看文献[4,8]等对Euler方程涡量-流函数形式的描述。由式(2)3和(2)4

其中GΩ(·,·)为区域 Ω 上的格林函数的负,即

其中 KΩ(x,y)=GΩ(x,y)。注意在 Ω×Ω 上,GΩ(·,·)< 0 ,GΩ(x,y)|x∈∂Ω=0 ,即 ∂Ω 是 GΩ(·,y)的0-等值线。所以∇xGΩ(x,y)与∂Ω垂直,指向Ω外,GΩ(x,y)与∂Ω 相切,指向反时针方向。在R2上式(1)的局部光滑解存在性定理,可参看文献[10]。我们将用到二维有界光滑区域上Boussinesq方程组的局部存在性定理:若ω和θ的初值ω0和θ0都在 C1(Ω),则存在T>0,使式(2)在 Ω×[0,T]上有C1解。可用类似于二维Euler方程的Yudovich定理的证明方法得到,可参看文献[5]和本文末段的概述。
以下描述本文中的尖点区域D'。我们沿用文献[7]中的区域(图1)。令
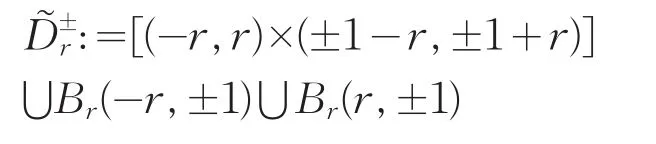
为两个分别以(0,1)和(0,-1)为中心的球场形区域,每个的高度是 2r>0(图1(a))。注意只是C1,1区域。通过在圆弧和直线段的接口处适当地改动圆弧,可得无穷光滑的区域。这个改动可以任意小,使和的面积任意接近。最后,令L ,其中 L=(-1,1)×{0}为开线段,用D:=表示D'的上半部,如图1(b)所示。
在D'上考虑式(2),设其上的光滑初值ω0和θ0对x2反对称,且在L的一个邻域内为0,则从光滑区域上的局部存在定理得到它们有互为正负的局部光滑解,由Dθ/Dt=0和Dω/Dt=θx1,容易知道对小的时间 t,ω(·,t)和 θ(·,t)在 L 的一个邻域内仍为0,所以两个解光滑地粘合成为D'上的局部光滑解。注:这样的在D'上的解的速度场u在x∈D处的值可由u(x,t)=(x,y)ω(y,t)dy给出。

图1 尖点区域
本文用Kiselev和Zlatos[7]的方法,在 D'上对无黏性无热传导Boussinesq方程组构造在有限时间内爆破的局部光滑解。与文献[7]中对二维Euler方程的讨论不同,从式(2)1可见,当θx1非零时(若要构造式(2)非平凡的解,θx1就不能恒为0),涡量不是简单地被搬运,而是随着流体质点的流动可以变动,以致变号,为估计边界上质点的移动速度增添了难度。本文通过选取适当的初始温度θ0,限制了在任何时候θx1≠0的区域的面积,从而解决了问题。
2 定理及其证明
在陈述主要定理前,先证一个引理。


又因为∂D在每个x∈∂D处都满足内球条件,所以由Hopf引理,对任意的x∈∂D,
(∇v·n)(x)=(∂v/∂n)(x)>0
从而 ∇v(x)≠0→,且因 ∂D 是紧的,所以
ε:=inf{ ||∇v(x),x∈∂D}>0断言得证。

以下我们完成引理1的证明。因为∂D是GD(·,y) 和 v(·) 的 0-等 值 线 ,所 以 对 x∈ ∂D ,∇xGD(x,y)和∇v(x)都与∂D垂直,都指向外。因此,在∂D上,对y∈
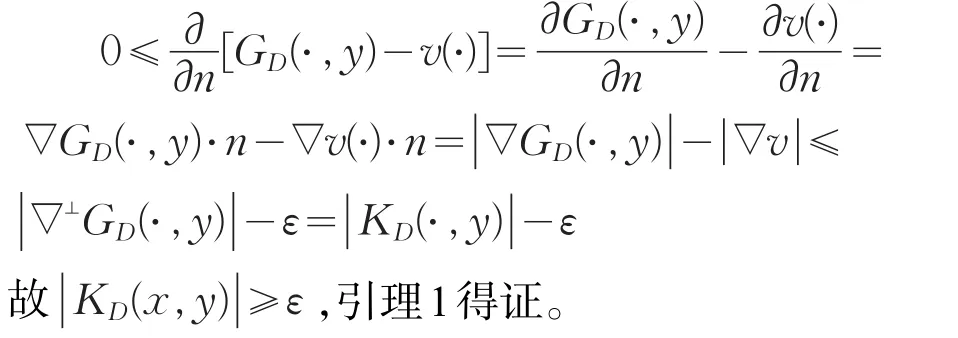
定理1带有尖点的区域D'上二维Boussinesq方程组(2)存在有限时间内爆破的局部光滑解。详细地,若初始温度和涡量 θ0, ω0∈C1(Dˉ')对 x2反对称,在L的一个邻域内为0,在D内它们非负,θ0只在足够小的区域上非0,ω0在θ0的支撑内不恒为零,且ω0在∂DL上与尖点P(图1(b))的距离足够小的一点处非0,则ω在有限时间内变得不连续。
证明:选取对 x2反对称的ω0,θ0,从而由Biot-Savart公式知速度场u相对于x1-轴对称,使在某时间t0>0前在∂D上的质点最低以某速度沿反时针方向流动,且在足够接近尖点P的某点x'∈∂D处ω0(x')>0,且保证从x'出发的质点流动时涡量不变。则从ω0对 x2的反对称性,当 x'与它相对于x1-轴的镜像x''同时流到L时,ω就在L处不连续。以下是详细证明。
第一步:选初始涡量和温度ω0,θ0:D'→R满足以下条件
(i) ω0,θ0∈C1(Dˉ'),对 x2反对称;
(ii)在 D 内,ω0,θ0≥0,不恒等于0;
(iii)ω0,θ0各在 L的某开邻域 Nω0,Nθ0内为0;
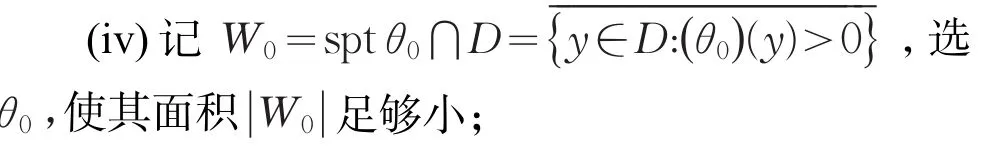
(v)∫W0ω0(y)dy>0 令,即 ω0在W0内不恒为0;
(vi)ω0在∂DL离P足够近的一点处非零(第三步中详细描述)。
设X(x,t)为从x出发的质点轨迹,即满足的唯一解。令

所以在 DWt上 ω(·,t)≥0 。事实上,若 ∉W0,则存在的一个邻域 N,N⋂W0=φ ,其上 θ≡0 ,从而θx1
≡0,Dω/Dt=0。因为 X(·,t)是 D 上的同胚,所以

第二步:由光滑区域上局部光滑解的存在性,可知存在T>0,使在 D×[0,T]上式(2)有以 ω0,θ0为初值的光滑解,若它在有限时间内爆破,则定理1结论已成立。以下设它可以延拓为D上的全局光滑解。
我们断言:若x∈∂D,u(x,t)=∫DKD(x,y)ω(y,t)dy 与 ∂D 相切,指向反时针方向,且存在常数C>0,t0>0,使当t∈[0,t0]时,有|u(x,t)|≥C。
为证明此断言,取δ>0,使
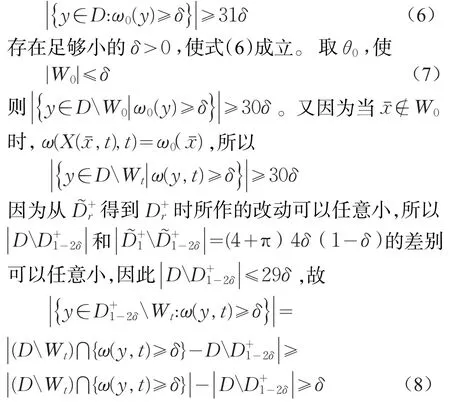
以上所涉及的区域可参看图2。把速度u分解为

图2 区域D,和Wt
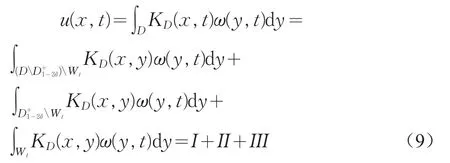
以下分别估计I,II和III。从式(4)后的讨论可知,对 x∈∂D,y∈D,KD(x,y)与∂D相切,指向反时针方向。因为在(D)Wt上 ω(y ,t)≥0,所以I指向反时针方向。对于II,同样地在积分区域里ω(y,t)≥0,令
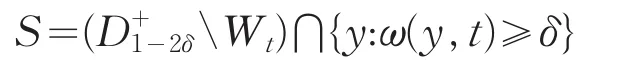
由式(8)可得,|S|≥δ,ω≥δ 。令τ为 ∂D 上指向反时针方向的单位切向量,则

由引理1,II是长度不小于εδ2,跟∂D相切,指向反时针方向的向量。以下估计III。由积分中值定理,

分以下两种情况讨论:若对所有 t≥0,ω(y0,t)≥0,则在任何时间III都指向反时针方向,得u(x,t)满足 |u(x,t)|≥εδ2,指向反时针方向的 ∂D 的切向量(此时取t0为任意正数)。若存在时间t,使ω(y0(t),t)<0,则令t0为使

第三步:从第二步可知直到时间t0,∂D上的质点沿反时针方向至少移动εδ2t0。现在选x'∈∂D,x'在令θ0消失的L的开邻域 Nθ0内(从而 x'∉W0,ω(X(x',t),t)=ω0(x')),并从x'沿反时针方向到尖点P的距离小于εδ2t0,那么在t0之前的某时间t1,从x'出发的质点将流到L中,又由ω对x2的反对称性(从而由Biot-Savart公式u1和u2分别对 x2对称和反对称),在上x'相对于 x1-轴的镜像 x''也同时流到 L。有两种情况:若 ω0(x')>0,则ω0(x'')<0,ω(·,t1)在 L 处将不连续;若 ω0(x')=0,则对ω0在x'附近作小改动使得ω0(x')>0,这样增加ω0后,I仍然指向反时针方向。对已选的δ,式(6)依然成立。所以在t0之前的某t1,仍有ω(·,t1)在L处不连续。定理1证毕。
以下粗略描述一般二维光滑区域Ω上Boussinesq方程组经典解的局部存在性。把式(2)补上u和θ的初值条件(10)5、 (10)6,把式(2)3、 (2)4换成等价的式(10)3、 (10)4后得到

存在性的证明平行于文献[5]中对二维Euler方程的讨论。先假定 ω0∈L∞(Ω),θ0∈C1(Ω),证明式(10)存在局部弱解,即存在T>0,及

n=1,2,…。可证式(12)有解,并在区域Ω×[0,T]内收敛到式(11)的解 ω,θ∈L∞(Ω×[0,T]),然后证明它们是式(10)的弱解。进一步,当ω0∈C1(Ω)时,可用类似于文献[5]的方法证明
ω,θ∈C1(Ω×[0,T])。
3 结论
本文考虑无黏性无热传导的Boussinesq方程组的全局正则性。通过粘合两个光滑区域上的光滑解,我们得到一个在带尖点区域上有限时间失去光滑性的局部光滑解。所以在这类区域上,这组方程组不具有全局正则性。

