一类脉冲时滞神经网络模型的周期性分析

张为元，王振华，张磊磊

（1.咸阳师范学院非线性科学研究所，陕西咸阳712000；2.京能锡林煤化有限责任公司，内蒙古锡林郭勒盟 026000）

在自然界中，许多生物系统处在周期变化的环境下，其动力学特征呈现出周期性。在神经网络系统中,具有周期系数的人工神经网络系统是一种重要的神经网络系统[1-3]，其在某种条件下会产生周期震荡现象。为了保证具有周期系数神经网络的稳定性，其周期解的相关性质，如解的存在性、稳定性等成为其重要研究内容。最近二十多年来，多种神经网络周期解的问题得到了广泛的研究，产生了许多重要的成果[1-6]。文献[5]利用线性矩阵不等式方法研究了一类离散时滞神经网络的全局周期性问题，并分别得到了时滞无关和时滞相关的周期性判据。文献[6]考虑的极限环可以通过存储模式应用到联想记忆中，因为一个平衡点可以看成具有任意周期振荡的特殊形式，所以神经网络的周期性研究具有重要性。

物理学、经济学、通信工程以及生物医学工程等许多科学和工程问题利用脉冲微分系统描述，为解决这些实际问题提供了数学模型。脉冲微分系统是一种特殊的不连续系统，被广泛应用到工程领域中控制系统的瞬时刻画，包括卫星变轨技术、工业机器人技术等。神经网络被广泛应用于图像处理、模式识别、联想记忆、信号处理以及保密通信等领域。此外，脉冲神经网络的相关理论和应用研究也是非线性系统理论研究的热点问题，引起了越来越多的学者的关注和深入研究。在实际问题中,由于记忆效应、开关速度和有限信号传输时间等神经网络的传输，可能会同时受到突变和时滞的影响，因而，对于具有周期系数的脉冲时滞神经网络模型开展深入研究也很重要。近年来，脉冲神经网络解的周期性问题得到广泛关注[7-10]。文献[7]研究了时滞神经网络周期解存在性和稳定性判据。文献[8]考虑了非时滞脉冲神经网络周期解的稳定性问题。文献[9]利用不等式和Lyapunov泛函的方法，讨论了带周期系数的脉冲时滞神经网络周期解的存在性和指数稳定性问题等。本文针对具有脉冲随机干扰时滞神经网络的周期性问题进行研究。利用Lyapunov稳定性分析方法和脉冲微分不等式等，建立考虑神经网络系统的周期解指数稳定性的充分条件。

1 模型描述与预备知识

考虑如下一类混杂神经网络模型

其中时间序列tk称为脉冲时刻且满足0＜t0＜t1＜…＜tk＜tk+1＜… ，=∞; ui(t)表示第i个神经元的状态；神经元之间的联接权值；n和F,{Ft}t≥0,P ) 表示激活函数；Ji表示外部输入；ai(t)表示与神经网络不连通且无外部附加电压差的情况下的第i个神经元恢复孤立静息状态下的速率；τ(t)表示时滞且0≤τ(t) ≤τ,τij(t),θji(t)是一常数；kij(·)是定义在(0 ,+∞ )上实值非负连续函数；ui(t-)和ui(t+)分别表示ui(t)关于t的左右极限；σij(·)(i,j=1，2，…，n)表示自由扰动的权函数；w(t)=(w1(t),w2(t),…,wn(t))T是一标准布朗运动；θik是常数。假设u(t)=u(t+)。ikik

系统（1）的初始条件如下

在系统（1）中，当 σij=0 时，文献[11]对该确定性模型进行了研究。当θik=0系统（1）变为具有混合时滞随机神经网络，文献[1，2，5]进行了研究。如果 θik=0和 σij=0，系统（1）归结为具有混和时滞的确定性连续系统。

本文我们作如下假设：

其中 j=1,2,…,n，Lf=diag()，=diag(，Lfˉ=diag()为正定对角矩阵。

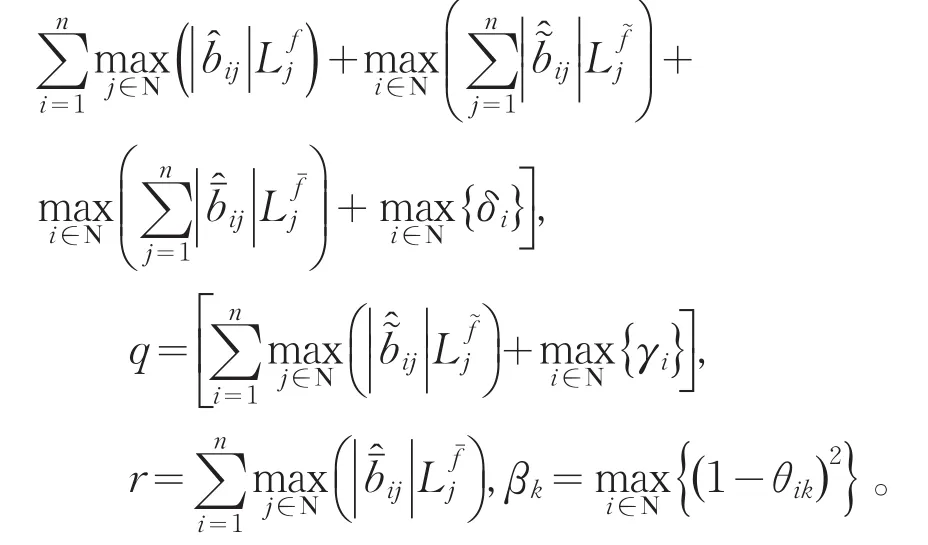
2 主要结果

定理 1 假设 (A1)-(A7)成立，则系统（1）和（2）的周期解在均方意义下全局指数稳定。

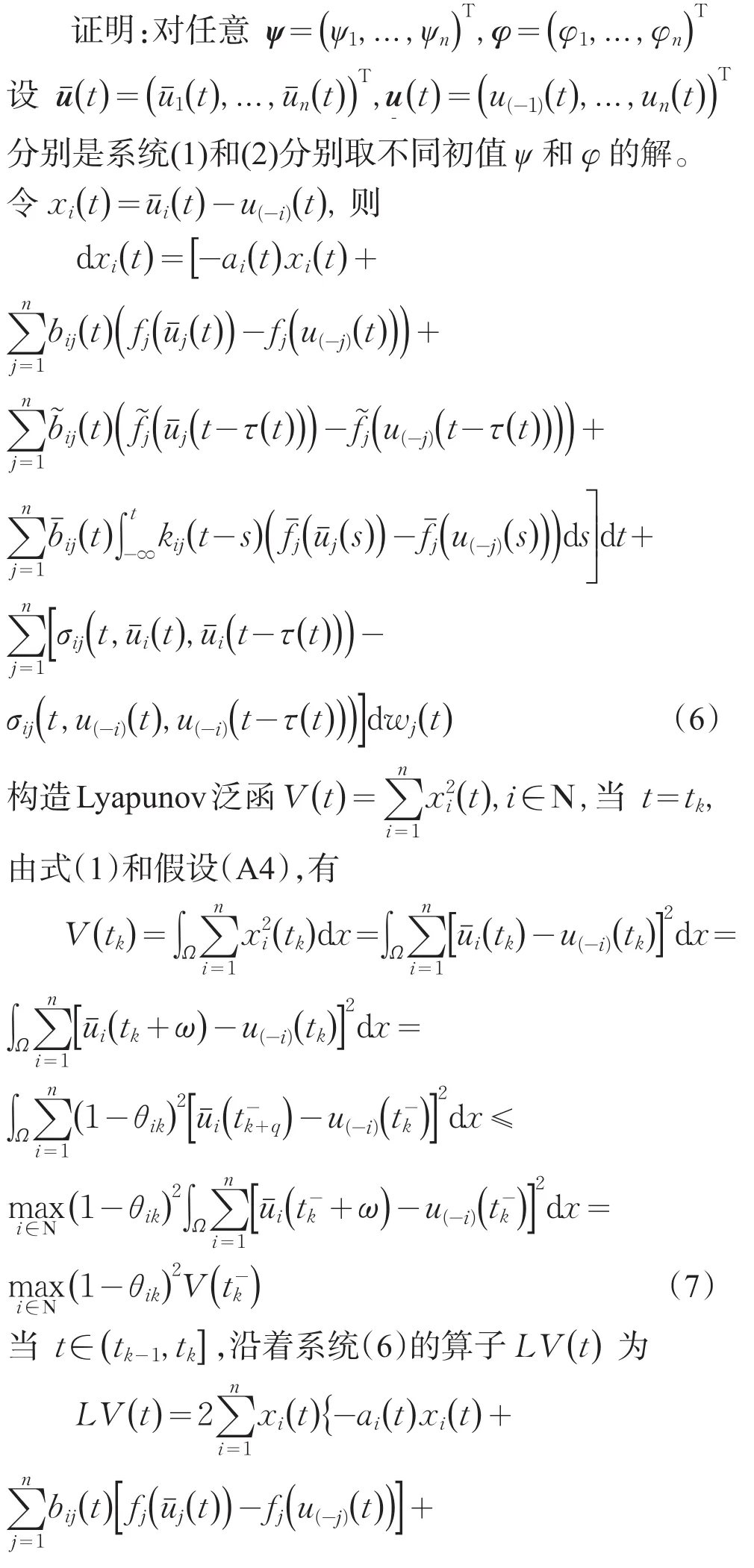
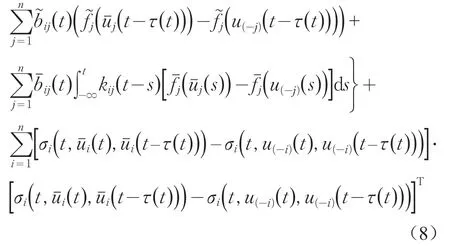
由Cauchy不等式和假设(A2)得

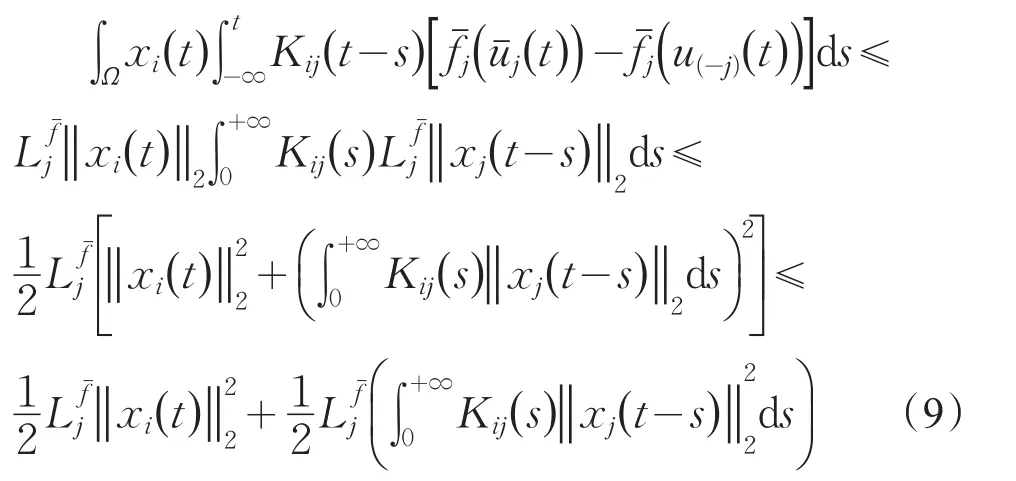
由假设 (A1)-(A3)、(A5)和式（8）（9）可得

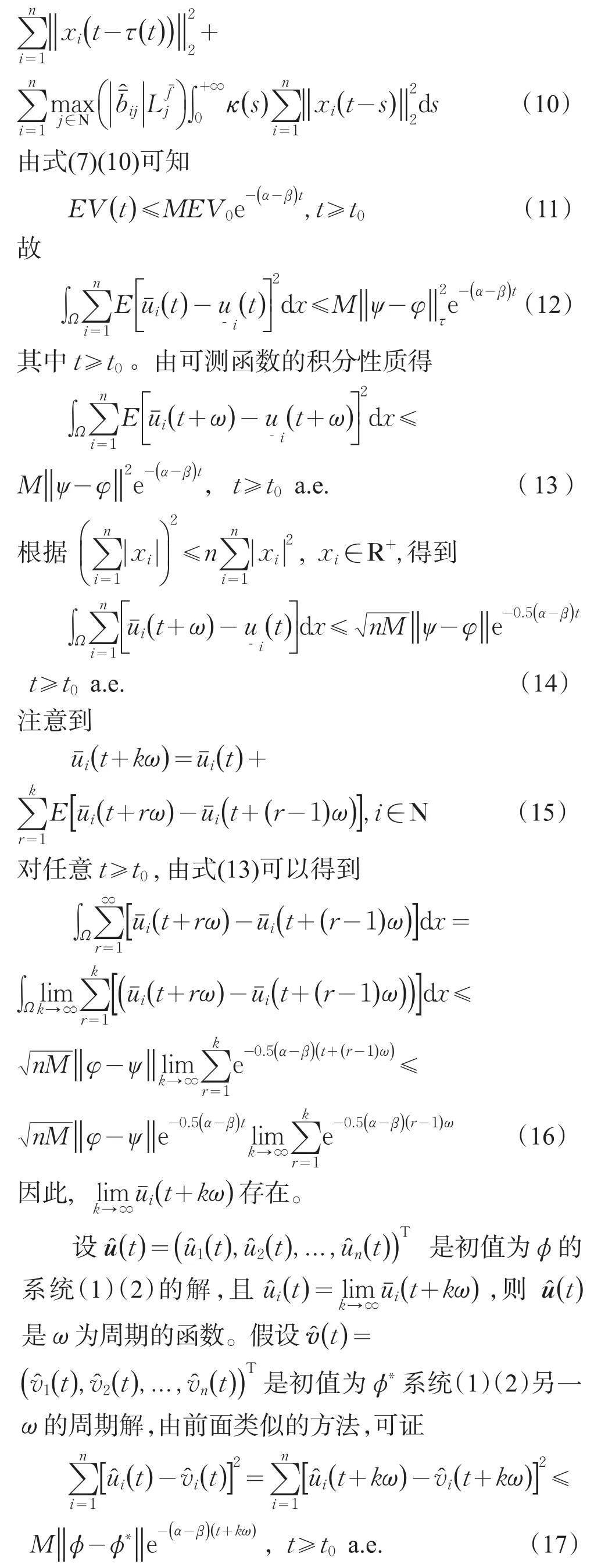
系统（1）（2）的周期解在均方意义下全局指数稳定。

定理2假设(A1)-(A3)和(A5)成立。如果存在正定矩阵 Ξ1,Ξ2,非负常数 p,q,r和 βk,(k ∈Z+),使得下列条件

证明：构造Lyapunov泛函如下

由式(11)和假设(A5)得

3 结语

本文考虑了脉冲随机时滞神经网络的周期性行为,即周期解的全局指数稳定性问题。构造适当的Lyapunov-Krasovskii能量函数，利用经典不等式和线性矩阵不等式，得到了该系统周期解的全局指数稳定的充分条件,对已有文献的结果进行了推广。