基于改进PSO与NB算法的软件缺陷预测模型

马振宇,张 威,*,王晓岭,高 飞,刘福胜

(1.装甲兵工程学院，北京 100072； 2.中国人民解放军91431部队，湛江 524002；3.中国人民解放军9596部队，武汉 430300)

0 引 言

近几年，随着科技的不断发展，软件在各个领域都得到广泛的应用，软件已然对国家经济走向以及国民生活品质的高低起到至关重要的影响作用。为了能最大限度的利用好软件，我们就需要在软件开发的第一步把好关，尽可能多的预测出缺陷，降低日后软件在使用过程中所需花费更大的代价。诸如软件的再次开发、维护成本甚至直接造成软件的失效，因此软件缺陷预测技术[1-3]越来越受到人们的瞩目。

为了寻找到一种高效地预测方法，可以更早地、更准地、更快地发现软件潜在的缺陷，那么就可以通过高效地预测技术节省更多的资源。本文借鉴遗传思想，将遗传算法中变异的思想融入到粒子群算法中，通过变异算子使得种群里的粒子更新得到更好地速度和位置；然后将该方法与朴素贝叶斯算法相结合，得到最优的分离点以及最低的错误率；最后建立软件缺陷预测模型，提高软件预测能力[4]。

1 相关工作

1.1 朴素贝叶斯

贝叶斯定理在250多年前就被发明，在当今领域内有着无法撼动的位置。贝叶斯分类是一系列该分类算法的统称，这些算法都是根据贝叶斯定理演变而来，所以都叫做贝叶斯分类。在该分类算法的领域里，朴素贝叶斯算法(Naive Bayesian)[5]是其中应用最为广泛的算法之一，本文将其做以重点介绍。

借鉴概率和数理统计的思想将NB分类。NB是贝叶斯算法的一种特殊情况，它简化了属性变量之间的关系，即简化为相互独立。虽然这个条件在一定范围里制约了朴素贝叶斯算法，但是与此同时，朴素贝叶斯算法使得对参数的估计大量简化，并通常可以忽略数据丢失带来的影响，算法本身也就简单化了，因而从较广的范围上降低了朴素贝叶斯算法的复杂度。

朴素贝叶斯算法模型如下：每一个数据样本都有很多的属性，把它的所有属性构建成一个n维的特征向量X={x1,x2,…xn}，分别对这n个属性进行A1,A2,…An度量。假设有m个类Y={y1,y2,…ym}，对于给出的一个未知样本X，预估X隶属于具有最大后验概率的类里，那么NB算法将未知样本分到yi，也就是满足下式：

P(yi|X)>P(yj|X), 1≤j≤m,j≠i

(1)

其中P(yi|X)最高对应类的yi称作最大后验假定，由贝叶斯定理，得到：

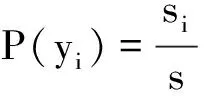
由于数据样本集具有很多的属性，它们之间的关系错综复杂，计算P(X|yi)的开销可能会异常的大，为了减少计算P(X|yi)的开销。我们假设各个属性相互独立，即在属性之间，没有任何联系，既有：

其中每个样本的属性条件概率P(x1|yi),P(x2|yi),…,P(xn|yi)可由训练样本估算。其中Ak分为两种情况讨论，即：

(1)若Ak是连续的，我们一般就假设这个属性满足高斯分布，得到：

其中，给出yi样本属性值Ak，g(xk,μyi,σyi)是属性Ak的高斯密度函数，而μyi,σyi分别为平均值和标准差。

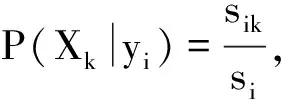
1.2 粒子群算法

粒子群算法[6-7]是人类根据鸟类群体的行为表象提出的一个算法，其核心思想就是模拟鸟类群体一起飞行寻食的过程，通过鸟类种群里各个小鸟的相互协作，反馈出自身最好的位置，然后再在鸟类种群里寻找到整个种群最佳的位置。现在我们把种群里的每一只鸟看成一个粒子，演化成现在的粒子群算法。就是在维数为D的搜寻空间里，有一粒规模数为N的种群粒子。然后规范粒子群相关参数，其中第i个粒子位置为：xi=(xi1,xi2,…,xiD)，第i个粒子速度为：vi=(vi1,vi2,…,viD)，第i个粒子历史最优位置为：pi=(pi1,pi2,…,piD), 所有粒子最优位置为：pg=(pg1,pg2,…,pgD)，位置更新公式为：viD(t+1)=ωviD(t)+c1r1×(pid(t)-xiD(t))+c2r2(pgD(t)-xiD(t))速度更新公式为：xiD(t+1)=xiD(t)+viD(t+1)。

2 基于遗传思想的PSO算法

为了保持粒子的高效性，根据遗传算法[8-10]里的变异算法，避免求解过程中陷于局部最优解。我们给出一个将变异思想融入PSO里的改进算法，即M-PSO(Mutation Swarm Optimization))。在历代更新进程中使用变异手段，使之最终得到最优解。

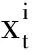
而PSO的具体变异迭代公式为：

(6)

在以上公式中，我们可以得出一些结论。第一块通过参数变量可以有效地预计变异的幅度和运动轨迹。第二块则是通过变异操作来达到目的的。

曾经有种极端的改变方法。将一部分粒子的原有运动轨迹直接变异为逆方向，大大增强了该群的多样性，提升了PSO的寻优能力。就是把遗传思想里的变异率应用到粒子群算法中，用种群的规模大小去乘以变异率，算出需要变异的粒子个数，选定等同数目的粒子个数，不再按原来的迭代方程式进行速度的更新，而是选取种群现状中最优解的逆方向定为该粒子的飞行轨迹。这样以来就扩大了粒子自身的搜寻范围，消弱了粒子聚集的可能性，避免了“早熟”现象的出现。

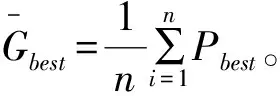
其基本实现步骤如下，即图1所示。

第一步：初始化该种群中所有粒子的初始位置和速度。假定粒子的种群数量为N。

第二步：通过适应值函数，算出每个粒子最初的适应值。将每个粒子在取适应值时所处位置设为Pbest，然后在根据该群体里的初始粒子，选择最优的适应值所对应的位置设为Gbest。

第三步：根据粒子位置和速度公式更新每个新粒子的最优位置和最佳速度。用其更新的位置和速度带入适应函数，计算出新的适应值。

第四步：判断β是否趋于0，如果是就对该代粒子采取变异手段，通过变异迭代公式去产生新的粒子,然后求解与其对应的新的适应值。否则直接跳过第五步，进行第六步。

第五步：比较所有适应值。把该代的每一个粒子的适应值分别于对应的上一代粒子乃至历代粒子的适应值进行对比，假如该代粒子的适应值比上一代粒子乃至历代粒子的适应值都要好，就把该粒子的位置更新为现在最好的位置，否则不进行替换。再拿下一代的每一个粒子的适应值去和历史全局的适应值进行比较，假如该带的适应值高于历史种群的适应值，就用该粒子的位置更换历史种群最优位置，否则不进行更换。

第六步：判别该方法的终止条件，如果算法大于最多迭代次数或者找到最优解，立刻终止。否则回到第三步，接着进行运算。

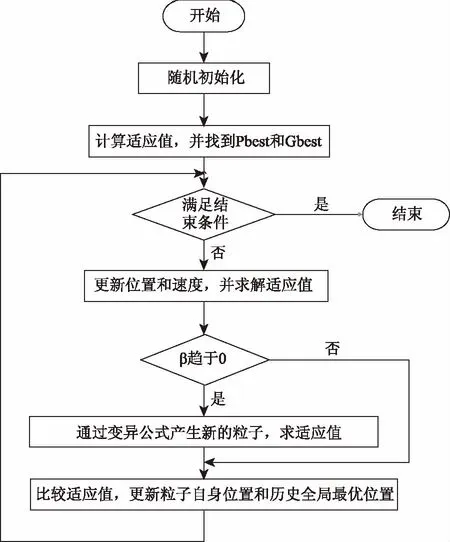
图1 M-PSO算法实现步骤

3 基于M-PSO与NB的软件缺陷预测模型

3.1 基于M-PSO与NB的属性离散化

把各个样本的属性值离散化，不但能够避免由于属性值连续带来的大量计算量，而且能使预测结果简单明了和便于应用。我们把M-PSO与朴素贝叶斯相结合来完成属性值连续问题的离散化。为了更好地叙述这个方法，我们不妨假定样本的属性数量为N。粒子群探索范围的上下界分别是：

Pmax=(pmax1,pmax2,…,pmaxN)

Pmin=(pmin1,pmin2,…,pminN)

(7)

其中Pmaxi和Pmini分别代表该样本第i个属性的最大值(上界)和最小值(下界)。各个样本的属性值的离散化其实就是在每个属性所属的范围内寻找几个分离点，假设将属性划分出a个等级，那么就需要找到a-1个分离点。

3.2 M-PSO与NB实现介绍

各个样本本身的属性离散化本质就是找寻该样本的分离点，由于没有统一的方法能够使分离结果做到最好，所以这也是实现该问题的一个难点。我们将NB的分类错误率当做粒子群算法里的适应函数，使用本文提出的M-PSO算法搜寻能够使得适应函数值最小的来找到最佳分离点。

第一步：对种群的粒子进行初始化，粒子群维数为N=20,w=0.3,c1=c2=1.5,r1=r2为0到1的随机数。最大迭代次数为Tmax=50，初始迭代次数为t=0。然后把属性划分为3个级别，即有2个分离点。

第二步：依据每个粒子的坐标分离各个样本的属性，在应用朴素贝叶斯算法得到分类错误率，也是在比较该粒子坐标的好坏。然后更替粒子群里各个粒子最优位置以及种群最优位置。

第三步：按照文章里指出的M-PSO算法更替该粒子种群两个指标。

第四步：t=t+1，判别t是不是小于T，如果是，立刻回到第二步，否则继续。

第五步：输出最佳分离点和最小错误率，得到软件缺陷预测模型。

3.3 软件缺陷预测模型

建立软件缺陷预测模型，即图2所示。

第一步：收集软件数据，输入总样本数以及各样本属性。

第二步：求解各个样本属性的的最大值(上界)与最小值(下界)。

第三步：根据文献[11]中，葛贺贺给出的训练样本与测试样本的分配比例(3∶2)，本文为了方便进行实验结果的对比分析，所以选择一样的分配比例。然后随机进行样本的分组。

第四步：将M-PSO与NB算法相结合，计算每个样本的分离点，将样本属性离散化。

第五步:基于第四步的结果，建立软件缺陷预测模型。

第六步：输出预测结果。

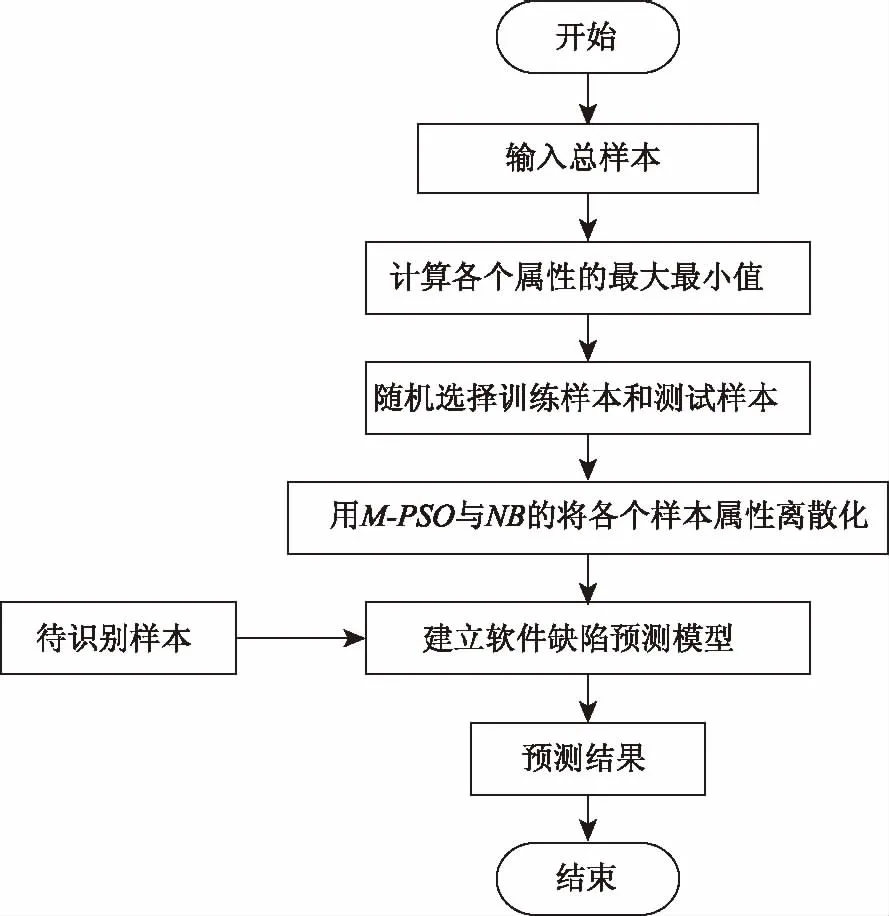
图2 软件缺陷预测模型

4 实验分析

为了更好地对比实验效果，本文采用NASA提供的数据包，里面总样本个数有10 855个，并包括21个属性。我们首先从总共的样本数里任意抽选6 000个当做训练样本，然后从剩余的里面任意抽选4 000个当做测试样本；然后根据数据离散化属性，从每个属性的最大值和最小值之间找出2个分离点，即把属性分为了3个等级；最后的实验结果如表1所示。

进一步我们可以得到分类错误率，在使用M-PSO与朴素贝叶斯方法相融合的情况下，使得错误率有了良好的改观，控制到15.12%。比其他算法计算出来的错误率更好。比如在文章《Knowledge Discovery in Databases: An Attribute-oriented Approach》[12]中的错误率为20.45%，在文章《Extracting Classification Rule of Software Diagnosis Using Modified MEPA》[13]中的错误率为18.87，而在极为相似算法的文章《基于PSO和朴素贝叶斯的软件缺陷预测模型》[11]中的错误率仍为16.8%，证明了该方法的有效性。

表1 数据离散化结果

5 结 语

本文通过将遗传算法里的变异思想融入到PSO中，提出了两个相融合的方法M-PSO，以此为基础，和朴素贝叶斯算法相融合，构建出软件缺陷预测模型。实验结果证明，由于M-PSO算法改良了粒子群算法本身收敛速度较慢的缺点，所以可以更加高效地预测缺陷，使得软件有了更高的可靠性。

但对于多样本多属性的数据，会出现收敛速度较慢的现象，所以在今后的研究工作中，需要采用更高效的分类算法，提高预测效果。