基于局部SVD的深度图像增强算法

冯 策, 薄 中

(中国电子科学研究院，北京 100141)

0 引 言

深度信息的获取是机器视觉中的重要步骤，无人机的碰撞检测和倾斜测量、移动设备的人脸识别等都依赖于对深度图像的分析。近些年，一些快速、经济型深度传感器[1]的诞生，为人机交互和机器视觉领域带来了一系列革命性的变化。由于深度信息与光和物体表面的反射特性无关，所以与传统图像相比，深度图像不受光照变化和阴影的影响。因此，深度图像更容易表示对象的特征，适合于提高机器视觉任务的可靠性和实时性。

然而由于采集设备获取的深度图质量不高，存在噪声严重、边缘缺失等问题，制约了其在工业领域的应用。所以如何改善深度图的质量是本文所要研究的问题。

1 问题分析

由传感器获取的深度信息主要存在以下三方面问题：

(1)深度图像的分辨率较低，不及彩色图像的分辨率；

(2)深度图像噪声干扰严重；

(3)深度图像在物体的边缘处容易出现缺失，通常是由于一个像素点所对应的场景包含了不同的物体表面所引起的。

在深度图像优化方面，至今已经提出了很多算法，文献[2]联合双边上采样方法，是从双边滤波法改进而来的，但是在引导图颜色相似的地方会导致深度图像的模糊，而且图像质量不高。文献[3]中的联合距离变换的方法改进了自适应核回归算法，优化了深度图像细节，但没有修复深度图像缺失。文献[4]利用多传感器数据融合和多向滤波器进行深度图像质量优化，但是需要基于多传感器组合，系统构建复杂。文献[5]分别采用不同尺寸的窗体对深度图像进行中值滤波，虽然可以填补不同大小的缺失，但是对边缘毛糙部分没有做平滑处理。文献[6]提出改进联合双边滤波法，引入梯度约束项进行图形优化，梯度比色彩具有更强的特征表示能力，引导图像梯度区域具有更好的约束作用。因此，针对传统深度图像增强算法存在的不足，本文提出了基于局部SVD的深度图像增强算法，以引导图像局部协方差矩阵分解后的奇异值作为增强标准，自适应的增强图像，同时结合非线性滤波法进一步优化深度图像的质量。

2 算法研究工作

2.1 基于引导滤波的能量函数

本文算法的能量函数是基于引导滤波器的彩色图像引导模式的，如式(1)所示。引导像滤波是何凯明提出线性保边滤波算法[7]，选取引导滤波法是因为其具有以下优点：

(1)线性滤波器，不依赖于滤波核大小，只依赖于像素数量；

(2)基于窗口的滤波，适用于GPU并行计算方式；

(3)可以有效抑制图像噪声；

(4)边缘以及细节的改善优于传统的保边滤波算法。

引导滤波器是利用引导图I来改善图像p的质量，在以像素点k为中心的窗口内局部线性变换：

ε‖ak‖2

(1)

ak=(CIp)(CI+εU)-1

(3)

bk=(U-ak)uk

(4)

uk=1/η∑j∈ω(k)Ij

(7)

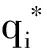
首先对待处理的深度图像进行邻域插值，将待处理深度图p的分辨率插值到与引导图I相同，然后最小化能量函数，确定线性系数，使得输出图像q和输入图像I的差别最小。深度图像包含三种类型的区域：边缘区域、平坦区域和细节区域。本文主要工作是对细节和边缘区域进行增强，滤除平坦区域的噪声，改善深度图像的质量。

2.2 面向深度图像的引导滤波法问题分析

引导滤波器中，在I=p和ε>0的情况下：

对于“细节和边缘区域”，也就是梯度值变化较大的窗口ωk，ak趋近于1，bk趋近于0。

通过以上分析，可知引导滤波器在梯度变化较大的区域，增强效果比较明显，而在平坦区域，平滑效果比较明显。深度图像中梯度变化较大的区域，通常是前背景边界处，但是这一部分在彩色引导图中的梯度变化可能很小，如图1(b)所示。因此，在这种区域，不仅达不到增强边缘的效果，还会导致模糊边缘的问题。

另一方面，在梯度变化较大的区域，引导图I与深度图p会很相似，如果此区域I的纹理比较复杂，而此区域的深度图像只是一条简单前背景分界线，滤波后的深度区域会因为接近于I，而影响深度信息准确性，导致区域出现混淆的情况，“混淆”区域在滤波过程中出现的比较频繁，是本文重点解决的问题。如图2(b)所示：

图1 “模糊”区域

图2 “混淆”区域

总结起来，面向深度图像的引导滤波器存在以下两方面的问题：

(1)彩色引导图的前景和背景边缘部分颜色相似，导致滤波后的深度图像边缘部分模糊，无法区分前背景，如图1所示。

(2)引导滤波器是引导图像I与滤波输出q的局部线性滤波器。纹理复杂的区域I与p会很相似，因此深度信息会受彩色图像影响，导致区域“混淆”，如图2所示。

2.3 局部协方差SVD的增强算法

由上节分析可知，系数ak主要决定滤波图像的细节部分，当增大ak值得时候，边缘和细节部分会得到增强，如图3所示：

图3 增大ak的效果

本文引入参数α来控制图像增强的效果，ak变为：

ak=α(CIp)(CI+εU)-1

(8)

随着α增大，边缘模糊的部分得到了增强，这样可以解决“模糊”区域的问题，但缺点是引导图纹理对于深度信息的影响也会随之增加，即“混淆”区域的增强，如图4中方框部分所示。为了解决“混淆”区域问题，本文引入了SVD分解算法。

SVD分解算法具有良好的稳定性和不变性，其分解的奇异值反映数据的内在属性，通常用于降低噪声，主元成份提取(PCA)，图像压缩的算法，搜索引擎语义层次检索的LSI。矩阵奇异值分解(SVD)属于矩阵对角化分解的一种，是针对一般矩阵的对角化分解算法，定义如下。

设A∈Rm×n，则存在正交矩阵：

U=[u1,…，um]∈Rm×m,V=[v1,…，vn]∈Rn×n

使A=UDVT

U是m*m阶酉矩阵，D为m*n阶对角矩阵，VT是n*n阶酉矩阵。其中：D=diag(s1,s2,s3,…,sn)，s1,s2,s3,…,sn为矩阵的奇异值，s1≥s2≥s3…≥sn≥0。

本文将引导图的局部协方差矩阵CI进行SVD分解：

UDUT=SVD(CI)

(9)

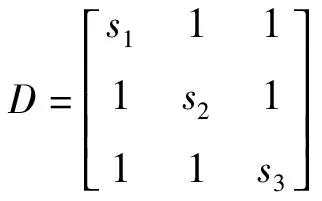
ak变为：

s1,s2,s3为CI的奇异值，代表局部区域梯度变化度的能量值，能量值越大，梯度变化越大，s1,s2,s3递减排列，其代表的区域梯度变化值也呈递减趋势。通常情况下，边缘区域是梯度变化较大区域，而混淆区域是相对边缘区域变化稍弱的区域，因此，本文联想到了利用奇异值所反映的属性来找到混淆区域，这也是本文算法的关键。

尝试缩小s2，滤波效果如图4所示。随着s2的减小，深度图像的“混淆”区域逐渐增强。

图4 减小s2的效果

由上图可见，s2是代表CI中混淆部分的奇异值，混淆区域是滤波过程中想要去除的区域，这也是本文最为感兴趣的部分，因此，可以利用这个特征来解决区域“混淆”的问题：

(1) 在s2较大的部分，即混淆的部分，α取较小值，减小“混淆”区域的增强。在s2较小的部分，即非混淆区域，α取较大值，增强非混淆区域。

(2) 增大奇异值s2和s3，削弱混淆和噪声。

根据以上分析，本文改进滤波模型，式(10)中的α改为自适应参数：

α=aexp(-s2τ)

(11)

α的值随着s2的减小而增大，混淆区域的s2较大，则α较小。经过一组图片的试验，式(11)中的参数a取3.5, τ取150。

式(10)中的D变为：

(12)

这里参考了ShinshuUniv的算法[8]，采用了指数模型对奇异值进行缩放，实验中β和γ分别取0.8和0.5。

2.4 联合双边滤波法优化

增强后的图像质量得到了改善，但是仍有部分混淆存在，如图5方框中所示，因此需要进一步的优化。

图5 未优化的效果

经典的保边滤波算法双边滤波法[9]，是在高斯滤波的基础上进行的改进，考虑了距离差异权重的同时，也考虑到了周围像素灰度差异权重。后期出现了联合双边滤波法[10]，联合双边滤波法的灰度相似性权重是基于引导图像进行计算的，而不是基于输入图像的。如下式所示：

其中Ip为结果图像，Iq为输入图像，g为灰度相似权重，d为几何相似权重。

针对深度图像的特点以及存在的问题，本文对双边滤波法进行了改进，具有以下功能：

(1)平滑无用的细节和噪声；

(2)联合彩色引导图对边缘进行优化；

(3)填补深度图像的缺失。

本文采用的联合双边滤波法是基于Lab颜色空间，权重因子是三个通道颜色差值，滤波器模型如下：

空间滤波算法是利用邻域像素的加权平均结果来填充中心像素，但是邻域中存在无效像素：一种是缺失像素；第二种是与待填充的中心像素不处于同一物体上的邻域像素。

处于同一物体上的像素可以利用颜色相似的权重因子来判断。而缺失像素的灰度值通常较小，因此，可以设定深度阈值来判定像素的缺失，小于阈值的则为缺失像素，对中心像素无贡献。因此，式(14)变为：

(16)

2.5 算法流程

本文基本算法流程如下：

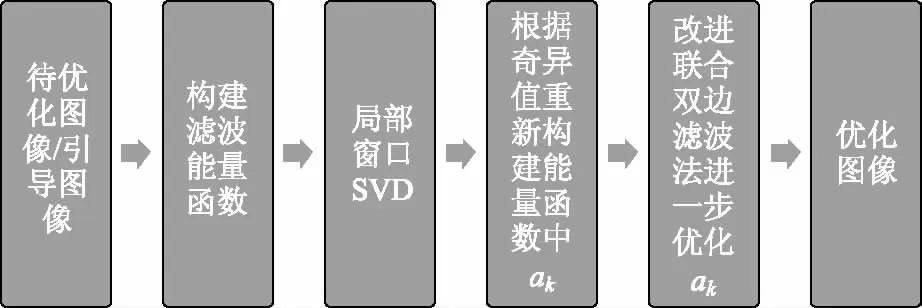
图6 算法流程图

(1)根据引导滤波构建算法能量函数；

(2)对引导图像进行局部协方差矩阵分解；

(3)将得到的奇异值作为能量函数核心参数的修正标准，自适应的优化图像；

(4)最后结合改进联合双边滤波法进一步优化深度图像的质量。

3 实验结果

在PC机器上，利用Python实现了本文提出的算法，计算机配置为Intel(R)Core(TM)i7CPU(3.3GHz) 8GB内存。实验数据采用了middlebury[11]标准数据集。标准数据集的彩色图像分辨率为1376×1088。

为验证本文方法的可行性与有效性， 就本文算法与联合双边滤波法计算结果以及真实深度图像进行比较。由图7(a)可见，原图像分辨率较低，噪声严重，质量较差。经过本文本算法优化后，深度图像的质量得到有效地改善，如图7(c)所示。与图7(b)的联合双边滤波法结果进行比较，本文算法的结果更接近于真实的深度图像。

图7 算法效果对比

4 结 语

本文提出了基于局部SVD的深度图像增强算法，对引导图像局部协方差矩阵进行SVD分解，并根据奇异值的大小自适应的增强深度图像，本文算法一方面增强了深度图像的细节，另一方面平滑了深度图像的噪声，有效地改善了深度图像的质量。在公开测试集上验证本文算法，并与真实深度信息以及联合双边滤波法优化结果进行了比较，本文算法对于质量较差(分辨率低，噪声严重)的深度图像优化效果较为理想，对于细节部分给予了很好的增强，但算法的缺点是在窗口尺寸较大的情况下比较耗时。