一种改进的独立分量分析跳频网台分选方法

杨芸丞, 孙雪丽, 钟兆根, 刘 军

(1. 海军航空大学，山东烟台 264001; 2.66135部队，北京 100144)

0 引 言

现代信息化战争中，跳频通信由于其低截获概率、组网方式灵活、信道衰减缓慢等优点，在军事通信、指挥、控制和情报系统均得到了广泛应用[1]。然而对于信号监听一方而言，如何在不具备一切先验条件的情况下，从混合信号中将多个跳频网台的信号分选出来，仍然是跳频通信侦察中具有挑战性的问题[2]。

传统的跳频网台分选方法多依据所截获跳频信号的纹理特征进行分选[3]。文献[4]引用模式识别的方法，搭建了稀疏贝叶斯模型进行分选，文献[5～10]等通过对跳频信号的跳周期、跳时、来波方位、功率等参数的准确估计聚类分选；文献[11]通过跳频信号驻留时间和起跳时间，建立分选的数学模型进行分选；文献[12]基于功率放大瞬态响应过程实现跳频网台分选。但在战场环境中，跳频信号的先验条件往往未知，且上述方法耗时较长，导致了这些方法的局限性，不能实时有效的达到战术战略目的。文献[13～15]将独立分量分析(Independent Component Analysis, ICA)引入跳频网台分选中，在未知跳频信号参数特征的情况下，实现了跳频信号网台的盲分选。但以往的独立分量分析方法未考虑跳频信号瞬时变化快、时频分析复杂等特点，选用的非线性函数不利于硬件实现，这就导致了上述算法鲁棒性能低，收敛速度慢，运算时间相对较长。

针对上述方法存在的不足以及跳频信号的特点，本文在快速独立分量算法[16]的基础上，提出了一种适用于跳频信号分选的改进的快速独立分量分析算法。该算法首先对传统的非线性多项式函数进行改进，建立一个基于负熵最大化的目标函数；其次将固定点算法的牛顿迭代[17]由二阶收敛转换为五阶收敛；最后以负熵最大[18]作为一个搜寻方向，顺序地提取了独立源，完成了对混叠跳频信号的分离。仿真结果验证了本文算法在不同信噪比、不同野值数目的适应情况，并与快速独立分量分析算法在相关系数、性能指标(Performance Index，PI)、输出信噪比指数、迭代次数、运算时间等参数做出性能比较[19～20]。

1 快速ICA算法

独立分量分析模型包括含噪线性模型和无噪线性模型[21]，本文主要使用含噪声线性模型。观测信号为含噪声的源信号的瞬时线性组合，则待处理的观测信号可表示为：

x(t)=As(t)+n(t)

(1)

其中s(t)为n维统计上相互独立的源信号矢量，s(t)=[s1(t),s2(t),…,sn(t)]T，x(t)为m(n≤m)维的观测信号矢量，x(t)=[x1(t),x2(t),…,xm(t)]T，n(t)为m维的噪声矢量，A为m×n维随机矩阵。ICA的目的就是寻找一个解混矩阵W，使得：

y(t)=Wx(t)=WAs(t)

(2)

式(2)中，y(t)是s(t)的估计矢量，当解混矩阵W是A的逆矩阵时，即WA=I，在未加噪声的前提下，由观测信号x(t)恢复成统计独立的源信号s(t)。

在对观测信号进行盲源分解前，通常都需要进行一些预处理，包括中心化和白化两部分内容。白化后观测向量记作z(t)，白化使原来所求的解混合矩阵A退化成一个正交阵，这种预处理方法使自由度从N2降为N×(N-1)/2，且算法收敛性更好。

对白化后的信号的分离，其目标函数采用一个经典的近似公式：

J(y)={E[G(y)]-E[G(yGauss)]}2

(3)

其中，E[·]为均值运算；G(·)为非线性函数，可取三个经典的非线性函数，分别为：

G2(y)=-exp(-y2/2)

(5)

a通常取1。

为找到一个独立分量或者投影追踪的方向[22]，采用定点迭代的方法，在WTz的方差约束为1的条件下，令WTz具有最大的非高斯性，负熵最大化目标函数如下:

J(y)={E[G(WTz)]-E[G(yGauss)]}2

(7)

根据Kuhn-Tucker条件，E{g(WTz)}的最优值能在满足下式的点上获得：

E{zg(WTz)}+βW=0

(8)

g1(y)=tanh(a1y)

(9)

g2(y)=yexp(-y2/2)

(10)

g3(y)=y3

(11)

利用牛顿迭代法解方程。用F表示式(8)等式左边的的函数，可得F的雅可比矩阵JF(W)如下：

JF(W)=E{zzTg′(WTz)}+βI

(12)

由于数据被白化，E{zzTg′(WTz)}≈E{zzT}·E{g′(WTz)}=E{g′(WTz)}I。因而雅可比矩阵变成了对角阵，得到下面的近似牛顿迭代公式：

(13)

其中，W*是W的新值，β=E{WTg(WTz)}，归一化能提高解的稳定性。简化后得到FastICA算法的迭代公式：

(14)

2 改进算法原理

2.1 非线性函数的改进

为获得E{g(WTz)}的最优值，采用自适应算法优化目标函数时，应满足(8)式的条件。将式(8)两端同乘WT，由于WTW=1，整理可得：

E{WTzg(WTz)}+β=0

(15)

由式(17)可以看出，WTzg(WTz)决定了算法的鲁棒性强弱，非线性函数的导数g变化越慢，算法鲁棒性能越稳定。

对选取非线性函数的考量，一是要考虑所选函数的硬件实现难度，二是要考虑所选函数对算法鲁棒性影响。前文提到的式(9)、(10)、(11)三个非线性函数，其中式(9)、(10)均为指数类函数，硬件实现较为复杂，运算时间长。而式(11)鲁棒性极差，一般不选用该函数。针对算法硬件实现难度和鲁棒性两方面考量，本文提出了一种新的非线性函数Tukey函数作为算法的目标函数。

Tukey函数具体表达式如下：

(16)

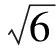
图1 四种非线性函数的导数图

由图1可以看出，非线性函数的导数g1(y)、g3(y)增长十分迅速，当存在较大的野值点时，函数值很难收敛。而g2(y)、g(y)增大到极大值点后又逐渐减小到零，当存在较大的野值点时，函数值趋向于零，这就很大程度上降低了野值对算法的影响，稳定了算法的鲁棒性。由于跳频信号频率跳变较快，对算法的鲁棒性能要求较高；为达到实时有效的网台分选，对硬件运算的实时性也提出了较高要求。通过上述的理论分析，考量函数的硬件实现难度以及鲁棒性能，应用独立分量分析的方法实现混叠跳频信号的网台分选，本文所提出的Tukey函数与传统的非线性函数相比，有明显的优势。

2.2 牛顿迭代法的改进

传统的固定点算法，是按照牛顿迭代公式所推导，得到快速独立分量分析的关键步骤式(14)，牛顿迭代公式如下：

为了提高算法的收敛速度，减少算法的运算时间，对快速独立分量分析算法的迭代公式就要作出改进，也就是要增加牛顿迭代公式的阶数。文献[17]给出了三种不同的三阶修正牛顿收敛公式：

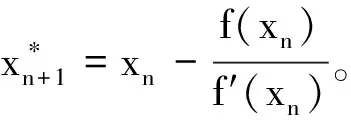
通过泰勒公式推导展开，利用式(18) 、(19) 、(20)分别得到三种五阶收敛的牛顿迭代公式：

(21)

(22)

(23)

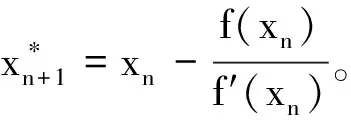
(24)

3 算法流程

按照上文改进的快速独立分量分析算法原理，具体的算法流程如下：

步骤一：对观测信号x进行中心化，使它的均值为0；再对中心化的数据白化处理得到z(t)。

步骤二：随机选择一个具有单位范数的初始权矢量Wp。

步骤三：设迭代次数p初始值为1，设需要估计的分量个数为n。

步骤四：将Wp代入式(26)，取G(y)=

步骤六：若Wp收敛，加上均值得到源信号；Wp不收敛，返回步骤四。

步骤七：令p=p+1，如果p≤n，返回步骤三，进行下一个独立分量的估计。

通过上述实现步骤，可以根据观测信号估计出源信号。

4 仿真实验与分析

实验一：本文算法的有效性验证

针对本文提出的改进的独立分量分析算法，对混叠跳频信号进行网台分选实验。一般来说，分离过程中，采样点越少，信号恢复的程度越差；源信号的差异性越小，分离越难实现。本文中信号源由三组不同频率集的同步正交跳频网台产生，有效降低了异步非正交跳频网台的差异性。三组跳频信号跳频速率同为250 hop/s，采样率同为10 kHz，抽取前320个点作为实验样本。本文中的仿真跳频系统可视作FH/8FSK调制跳频系统。

三组归一化跳频频率集分别为：

fk1=[0.10,0.45,0.30,0.05,0.20,0.40,0.25,0.15](kHz)

(25)

fk2=[0.32,0.12,0.21,0.36,0.14,0.23,0.17,0.42](kHz)

(26)

fk3=[0.22,0.33,0.44,0.18,0.06,0.31,0.41,0.08](kHz)

(27)

为仿真3个不同位置接收机的观测信号，本文中随机混合矩阵设置为：

(28)

仿真后，得到图2所示的源信号图，图3所示的观测信号图。图例中，FastICA-G1(y)、FastICA-G2(y)、FastICA-G3(y)分别代表基于非线性函数G1(y)、G2(y)、G3(y)的快速独立分量分析算法。

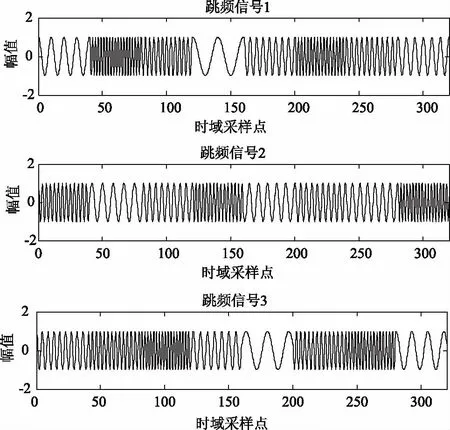
图2 跳频信号源信号

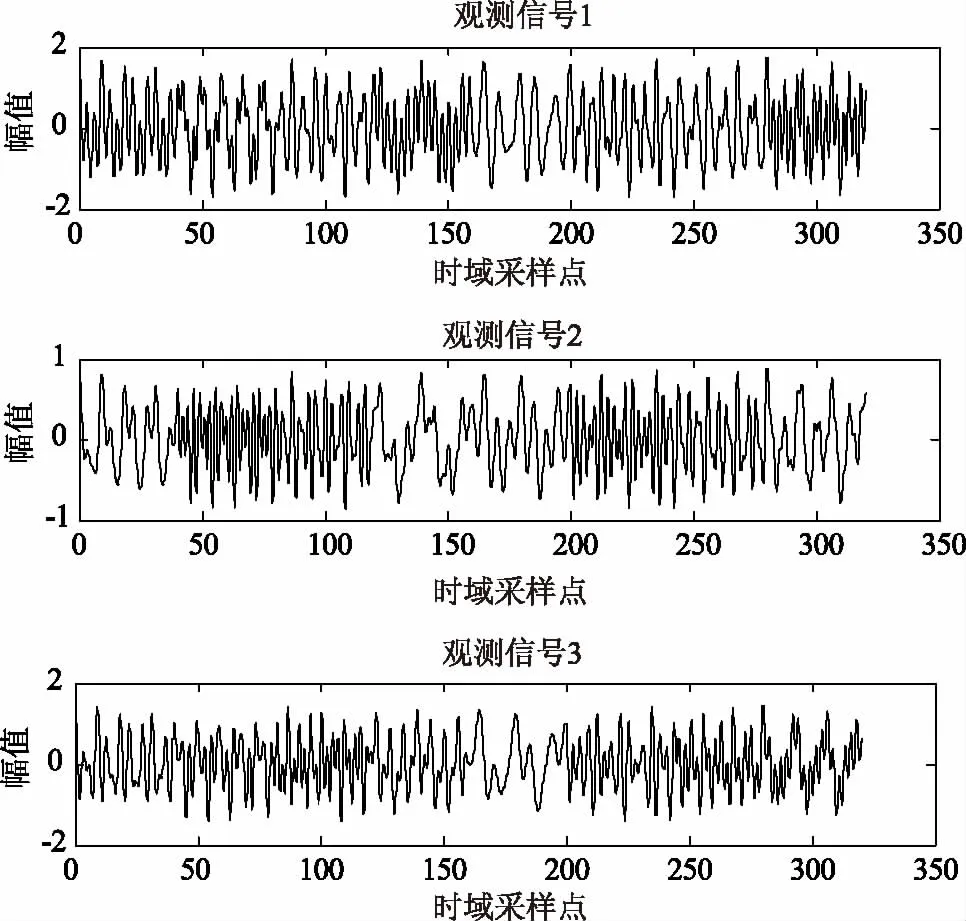
图3 观测信号

分别根据本文算法及以式(4) 、(5)、(6)作为非线性函数的快速独立分量分析算法对图三中的观测信号进行处理。

上述方法分别实现了对跳频混叠信号的分选。对上述方法进行比较，一方面，本文算法分离的信号与源信号相比，恢复程度要好；另一方面，上述算法均存在采用独立分量分析方法的两种问题：一是分离信号的次序较源信号发生了变化；二是分离信号的幅度和相位发生了不同程度的变化。但这两种问题并不影响对跳频信号网台的分选以及主要参数的识别。实际的跳频信号比本文仿真实验产生的跳频信号仍要复杂，对信号的恢复程度会有更高的要求，本文算法有效的提高了跳频源信号的恢复程度。

实验二：本文算法对不同信噪比的源信号的适应情况分析

通过实验一，我们可以将不同算法分离出的信号波形与源信号作对比，但这只能定性的分析不同算法分选性能的优劣[23]。为了定量的检验各独立分量分析的性能，本文引入相关系数、性能指标PI值、信噪比指数三个指标作对照分析。

相关系数定义[16]如下：

(29)

其中，|ρij|越接近1时， 两曲线越线性相关；|ρij|越接近零时，两曲线越线性无关。本文中，进行1 000次蒙特卡洛实验取平均值，通过比较各算法在不同信噪比条件下分离后的解混信号与源信号的相关系数，验证算法的优劣程度，相关系数取三组信号相关系数中绝对值的最小值。

图5给出了各算法不同信噪比下源信号与分离信号相关系数比较图。通过图5可以看出，本文提出的改进的独立分量算法相关系数在各信噪比条件下明显优于FastICA-G1(y)、FastICA-G2(y)、FastICA-G3(y)，且曲线更加平滑。

性能指标PI值[20]定义如下：

式(30)中：混合分离矩阵C=WHBA=(cij)n×n。W是白化后的分离矩阵，B是白化信号，A是随机混合矩阵。PI值越小，盲源分离的效果越好。本文中，进行1 000次蒙特卡洛实验取平均值，通过比较各算法在不同信噪比条件下分离后的解混信号与源信号的性能指标PI值，验证算法的优劣程度。

图6给出了各算法不同信噪比下源信号与分离信号性能指标PI值比较图。通过图6可以看出，本文提出的改进的独立分量算法相关系数在各信噪比条件下PI值较低，故改进的独立分量分析算法性能明显优于传统的快速独立分量分析算法。

图4 不同算法分离的跳频网台分选图比较

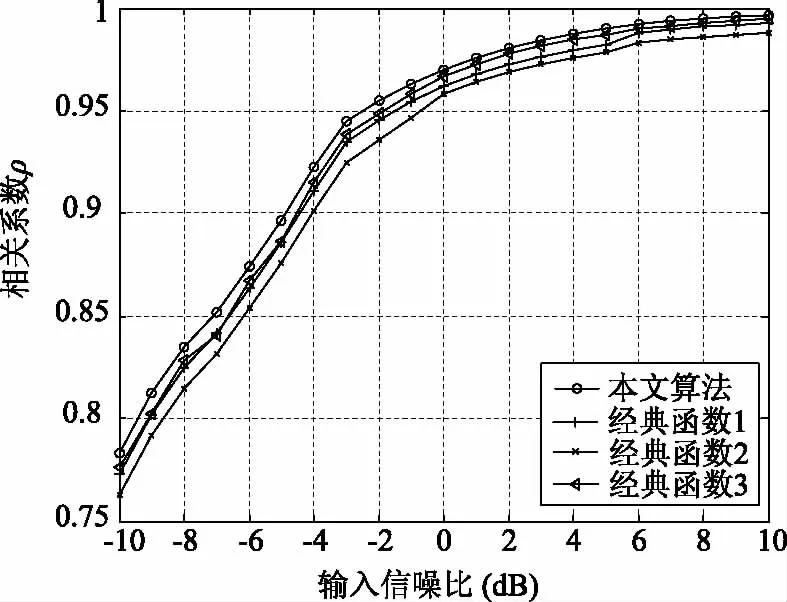
图5 各算法不同信噪比下源信号与分离信号相关系数曲线

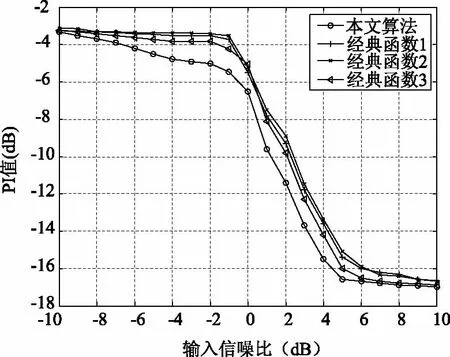
图6 各算法不同信噪比下源信号与分离信号PI值曲线

信噪比指数定义[16]如下：

其中var代表对向量进行方差计算，si为源信号矢量，sj为分离信号矢量。该参数越大，证明盲源分离效果越好，源信号与分离信号越接近。

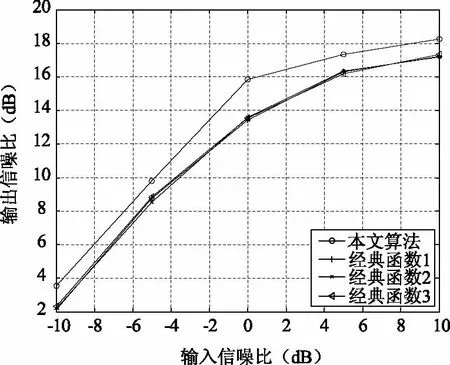
图7 各算法不同信噪比下源信号与分离信号输出信噪比指数曲线

图7给出了各算法不同信噪比下源信号与分离信号输出信噪比指数比较图。通过图7可以看出，本文提出的改进的独立分量算法相关系数在各信噪比条件下输出信噪比指数高于传统的快速独立分量分析算法。

综合相关系数、性能指标PI值、信噪比指数三个指标作对照分析，本文算法均优于FastICA-G1(y)、FastICA-G2(y)、FastICA-G3(y)。究其原因是，跳频信号频率变换迅速，需要很好的稳定性，本文采用的Tukey 函数一阶导数g(·)超过阈值之后其输出值逐渐减小，直到零为止，且一阶导数变换速度较慢，从而算法性能稳定；另一方面，牛顿迭代速度由二阶变为五阶，算法迭代次数会明显减少，这很大程度上加快了收敛速度。

实验三：本文算法的鲁棒性分析

图8给出了各算法野值数目与性能指标PI值关系曲线图，PI值计算公式如式(30)。通过比较各算法在不同野值数目的情况下，分离后的解混信号与源信号的性能指标PI值，验证各算法的鲁棒性能，图中记录的数值均为1000次蒙特卡洛实验后的平均值。实验中，选用的野值由 [0,3] 之间均匀分布的随机变量产生。

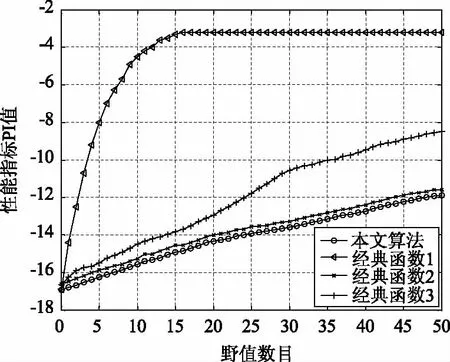
图8 各算法野值数目与性能指标PI值的关系曲线图Fig.8 The number of outliers and PI value of the relationship between the graph

通过图8可以看出，一方面，在不同野值数目的条件下，本文算法均取得了最好的性能指标；另一方面,本文算法的性能指标的变换量也是最小的，这就进一步验证了本文算法相比于其他算法有更好的鲁棒性能。不得不提到的是，在实验中，基于FastICA-G2(y)的快速独立分量分析算法也具备良好的鲁棒性能，但是FastICA-G2(y)为指数类函数，硬件实现较为困难，也影响了算法的运算速度、增加了网台分选的分选时间，这一点在实验四中得以体现。

实验四：本文算法的计算复杂度分析

各算法迭代次数与分选时间的比较见表1。表中各数据均为1000次蒙特卡洛实验取平均值。

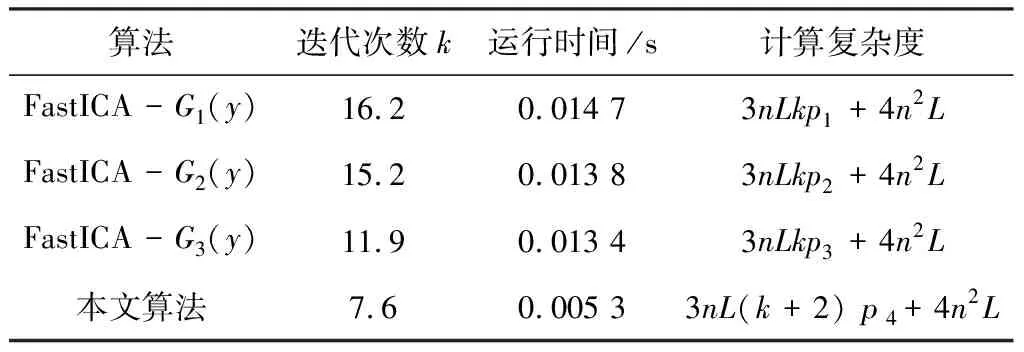
表1 各算法迭代次数与分选时间对照

分析四种算法的计算复杂度，将一次乘法或一次加法的计算复杂度记为1，四种算法在一次迭代时计算复杂度分别记作p1，p2，p3，p4，且p2>p1>p3>p4，源信号矢量的维数为n，L为采样数目，k为迭代次数。在白化过程中，四种算法的计算复杂度均为4n2L；在固定点算法时，基于非线性函数G1(y)、G2(y)、G3(y)的快速独立分量分析算法的计算复杂度主要集中于式(14)，分别为3nLkp1,3nLkp2,3nLkp3。基于本文算法的计算复杂度主要集中于式(24)，计算复杂度为3nL(k+2)p4。

5 结 语

本文以跳频网台分选为研究对象，在推导传统的快速独立分量分析方法的基础上，改进了目标函数的非线性函数，增加了固定点算法牛顿迭代的次数，提出了一种改进独立分量分析算法的跳频网台分选方法。仿真实验验证了本文算法的性能。由本文的仿真实验分析得出：在不同信噪比条件下，本文算法的相关系数、性能指标PI值、信噪比指数均优于传统的独立分量分析算法；本文算法鲁棒性能得到提高、收敛速度加快、运算时间减少60%以上。相较于传统的快速独立分量分析方法，本文提出的改进的独立分量分析算法更适用于对混叠跳频信号进行网台分选。本文算法可以在正定或者过定的条件下完成跳频网台的盲分选，今后的工作中，将结合ICA降维的方法，实现在欠定条件下的跳频网台盲分选。