浮标CODAR阵探测定位精度分析

何建伟,蔡爱华

(中国电子科学研究院，北京 100041)

0 引 言

声呐浮标是对水下潜艇进行搜索、跟踪和定位的重要手段。被动全向声呐浮标由于搜索效率高，隐蔽性好，使用方便等优点[1]，尤其适合于航空反潜。但被动全向声呐浮标只具备探测目标有无的能力[2]，获知目标定位信息需通过多枚浮标组成CODAR(Correlation Detection And Ranging)阵来实现[3]。本文采用基于几何精度衰减因子(GDOP)的定位精度模型，分析CODAR阵探测过程中各误差源对定位精度的影响。从CODAR对的时延测角原理出发，分析时延误差、水中声速误差及浮标对间距误差对测角精度的影响；考虑到工程应用带来的布阵误差[4]，分析其对CODAR阵定位精度分布的影响；给出综合考虑各误差源时CODAR阵的定位精度分布结果。分析结果对航空反潜中浮标的应用具有一定参考意义。

1 CODAR探测原理

CODAR探测原理示意如图1所示。

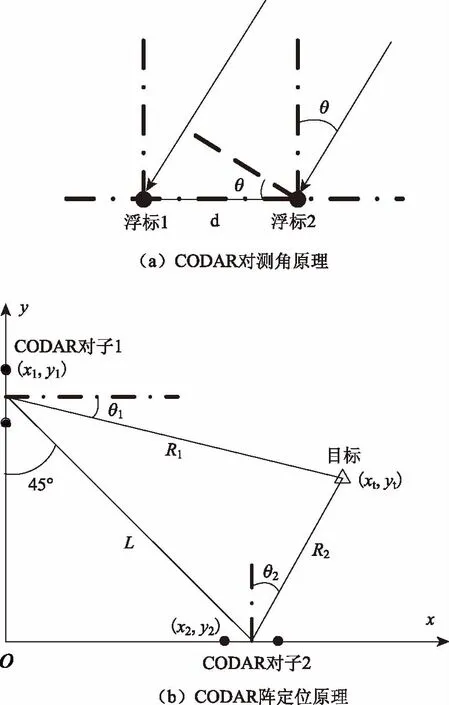
图1 CODAR阵工作原理

由图1(a)，有如下关系：

式中，c为水中声速，t为两浮标间信号到达时延，d为两浮标间距。由此得到：

(2)

如图1(b)所示，建立直角坐标系xoy。设CODAR对子的中心位置坐标分别为(x1, y1)、(x2, y2)，CODAR对测量得到的目标方位角分别为θ1、θ2，目标的位置坐标为(xt, yt)。由几何关系可以得到：

(3)

由CODAR对子的中心位置(x1, y1)、(x2, y2)以及方位测量值θ1、θ2，利用上式计算获得目标位置(xt, yt)。

以GDOP(GeometricalDilutionofPrecision)描述定位误差的空间分布[5-7]，即目标在空间不同位置时定位误差的大小，由下式确定：

2 CODAR测角误差分析

由公式(2)，测角误差Δθ由时延误差Δt，水中声速误差Δc，及两浮标间距误差Δd引起。考虑到各误差源相互独立，得到：

由公式(1)、(2)，各误差源引起的测角误差取值分别为：

(6)

其中，两浮标间距误差Δd由浮标投放误差决定，水中声速误差Δc与水文环境有关，时延误差Δt由测量系统决定。

综合考虑各误差源时，CODAR阵的测角误差取值为：

2.1 时延误差

仅考虑时延误差时，在典型的水中声速c=1500 m/s、浮标间距d=200 m条件下，不同时延误差Δt对测角误差Δθt的影响如图2所示。

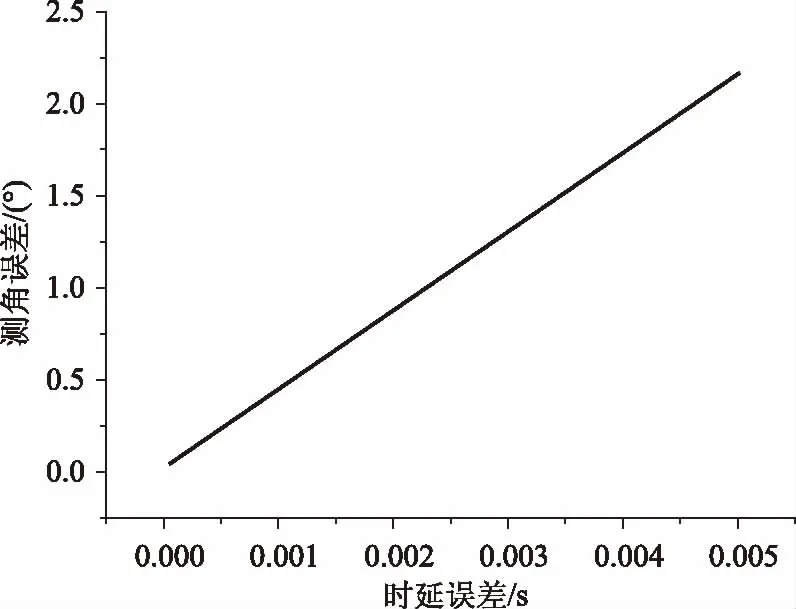
图2 时延误差Δt对测角误差Δθ的影响

假设浮标作用距离3000m，CODAR对子距离d=200m，水中声速C=1500 m/s，当CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位：m)时，测角误差[-0.5°，0.5°]范围分布区域如图3阴影部分所示。

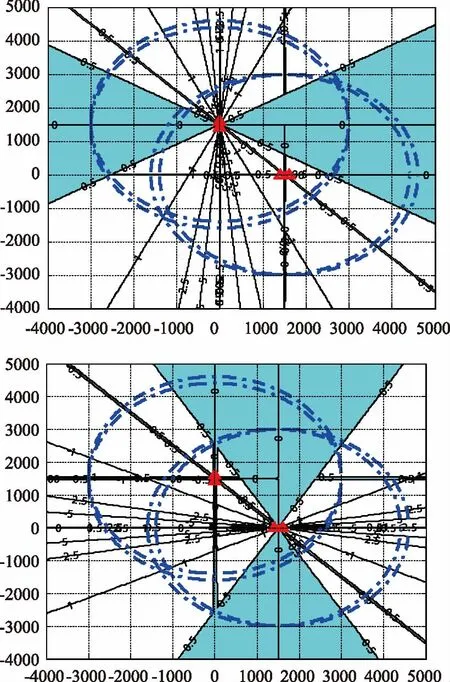
图3 时延误差t=1ms，测角误差[-0.5°，0.5°]分布

从图3看出，因时延误差产生的测角误差，其分布范围以CODAR对中心垂线为轴对称分布，靠近中心垂线的区域测角误差最小，随着测量方向偏离CODAR对中心垂线，测角误差逐渐变大。

2.2 水中声速误差

仅考虑水中声速误差时，在典型的水中声速c=1500m/s、浮标间距d=200m条件下，不同水中声速误差Δc对测角误差ΔθVc的影响如图4所示。

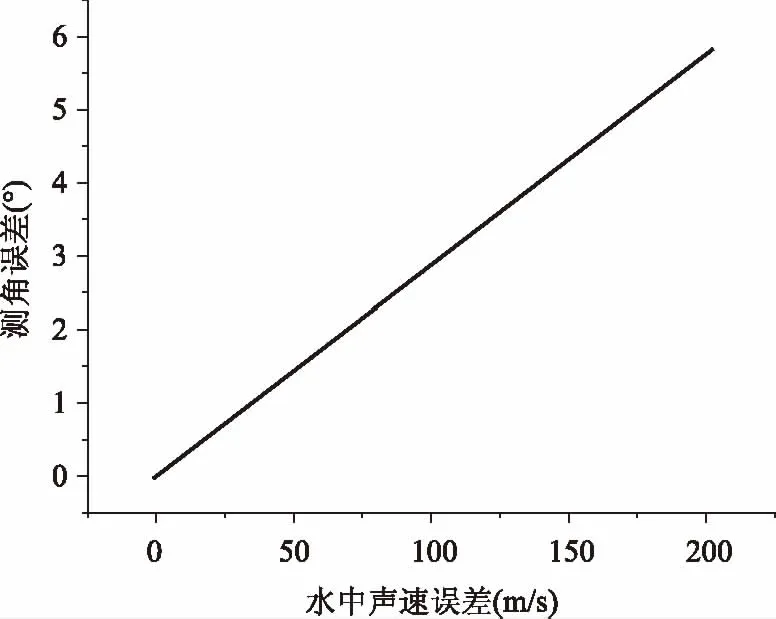
图4 水中声速误差Δc对测角误差Δθ的影响

假设浮标作用距离3000m，CODAR对子距离d=200 m，水中声速C=1500 m/s，当CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位：m)时，测角误差[-0.5°，0.5°]范围分布区域如图5阴影部分所示。

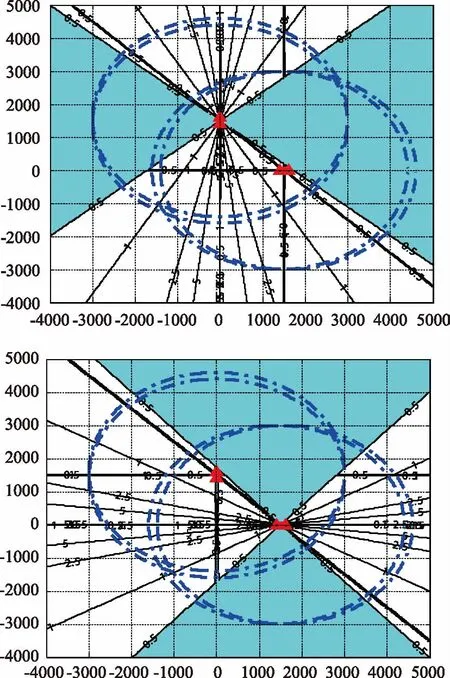
图5 水中声速误差c=15 m/s，测角误差[-0.5°，0.5°]分布

2.3 浮标对间距误差

仅考虑浮标对间距误差时，在典型的水中声速c=1500 m/s、浮标间距d=200 m条件下，不同浮标对间距误差Δd对测角误差Δθd的影响如图6所示。

对于2m浮标对间距误差，即Δd=2 m，Δθ=0.43°。

假设浮标作用距离3000m，CODAR对子距离d=200 m，水中声速C=1500m/s，当CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位：m)时，测角误差[-0.5°，0.5°]范围分布区域如图7阴影部分所示。

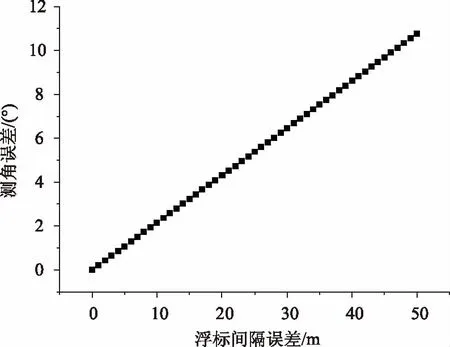
图6 浮标对间距误差Δd对测角误差Δθ的影响

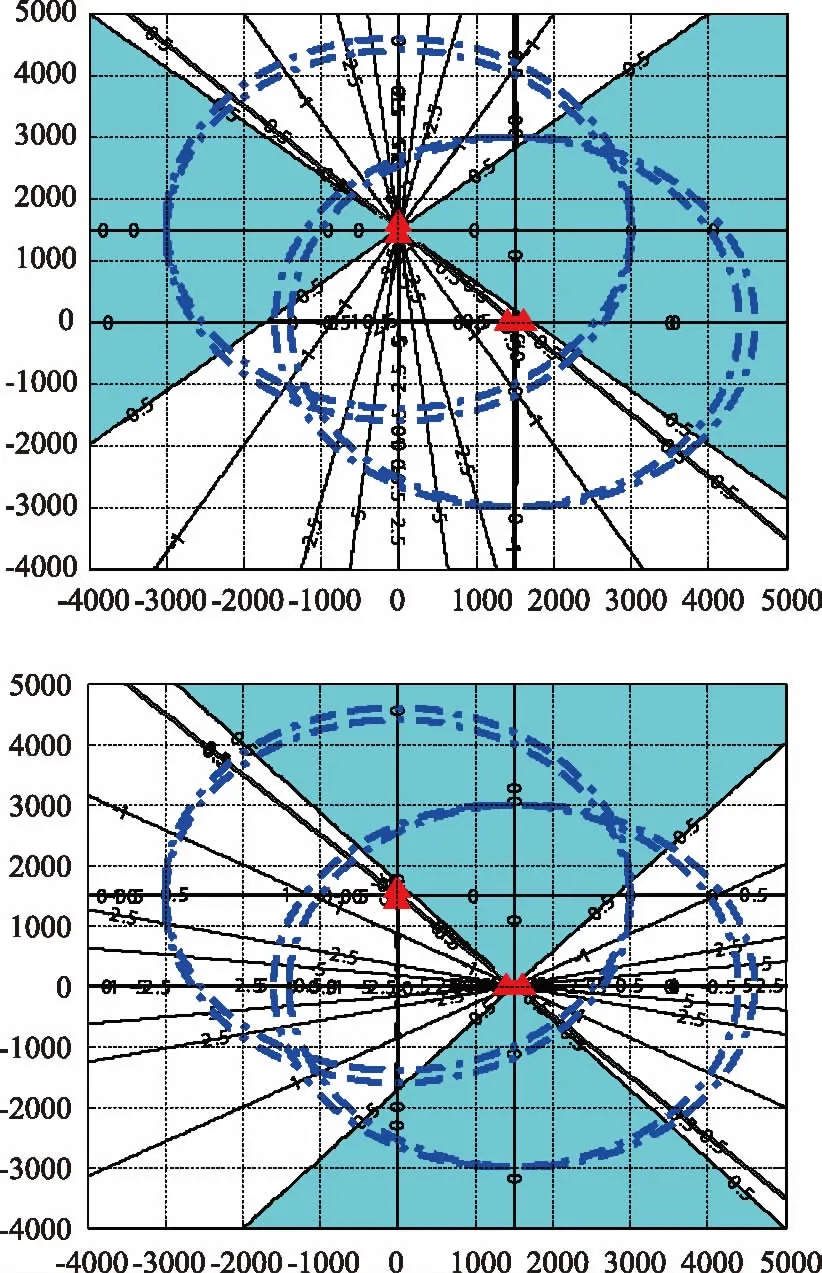
图7 浮标间距误差Δd=2 m，测角误差[-0.5°，0.5°]分布

对比图3、5、7，由各误差源引起的相同测角误差(Δθ=0.43°)条件下，对于[-0.5°，0.5°]范围的测角误差，由时延误差产生的分布区域最小。为使测角误差小于0.5°的区域尽可能的大，应优先考虑减小时延误差。

3 CODAR阵定位精度分析

对如图1(b)所示的CODAR阵，其定位精度分布与三种因素有关：1. CODAR对子的测角误差；2. CODAR阵的布阵误差；3. 两CODAR对子间的布阵间距。

3.1 测角误差对定位精度的影响

当测角误差的空间分布为定值时，图1(b)所示CODAR阵的定位精度GDOP空间分布如图8所示。假设CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位m)。浮标作用距离3000 m，测角误差Δθ1=0.5°，Δθ2=0.5°。图中阴影部分区域定位精度为100 m。

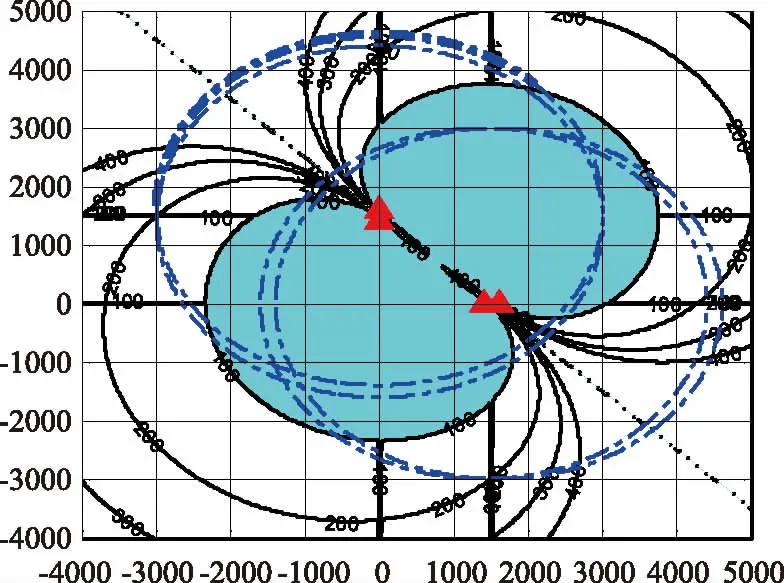
图8 测角误差Δθ1=Δθ2=0.5°时，CODAR阵定位精度分布

由图3、5、7，时延误差、水中声速误差及浮标对间距误差所引起的测角误差空间分布并非定值，考虑误差源带来的影响，CODAR阵的定位误差分布如下：

仅考虑时延误差时，假设CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位m)。浮标作用距离3000m。

当Δt=1 ms时，CODAR阵定位精度分布如图9所示，图中阴影部分区域定位精度为100 m。

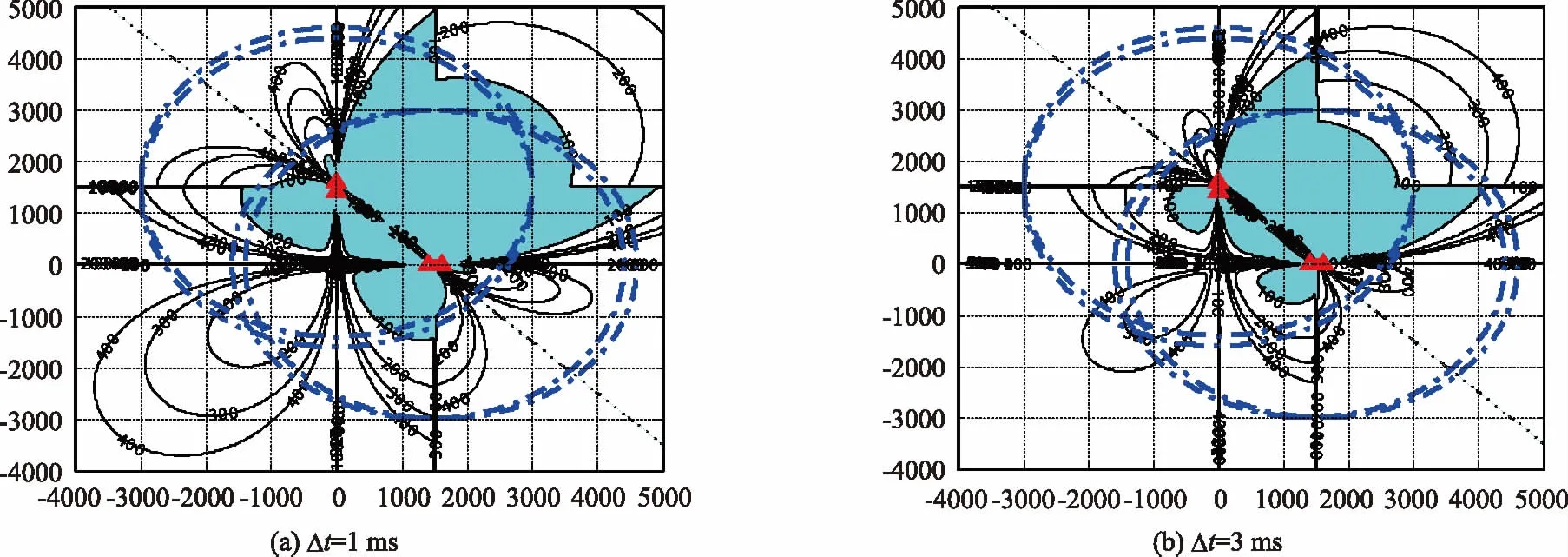
图9 时延误差对CODAR阵定位精度分布影响

由图9，随着时延误差的增大，CODAR阵定位精度高的区域向CODAR对子中心连线收缩，分布区域缩小。

仅考虑水中声速误差时，假设CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位m)。浮标作用距离3000 m。

当Δc=15 m/s时，CODAR阵定位精度分布如图11所示，图中阴影部分区域定位精度为100 m。

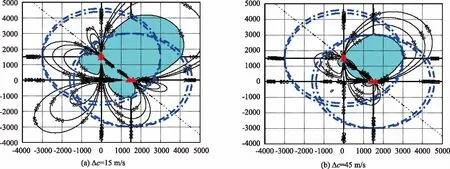
图10 水中声速误差对CODAR阵定位精度分布影响

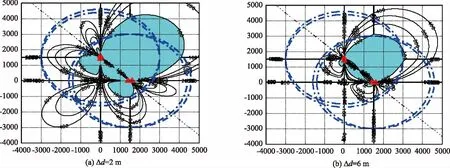
图11 浮标间距误差对CODAR阵定位精度分布影响

由图10，随着水中声速误差的增大，CODAR阵定位精度高的区域向CODAR对子中心连线收缩，分布区域缩小。

仅考虑浮标间距误差时，假设CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位m)。浮标作用距离3000 m。

浮标间距误差对CODAR阵定位精度分布的影响如图11所示，图中阴影部分区域定位精度为100 m。

由图11，随着浮标间距误差的增大，CODAR阵定位精度高的区域向CODAR对子中心连线收缩，分布区域缩小。

综合考虑各误差源所引入误差，假设CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位m)。浮标作用距离3000 m。各误差源的典型值为：时延误差Δt=1 ms；水中声速误差Δc=45 m/s；浮标对间距误差Δd=5 m。CODAR阵的定位误差分布如图12所示，图中阴影部分区域定位精度为100 m。

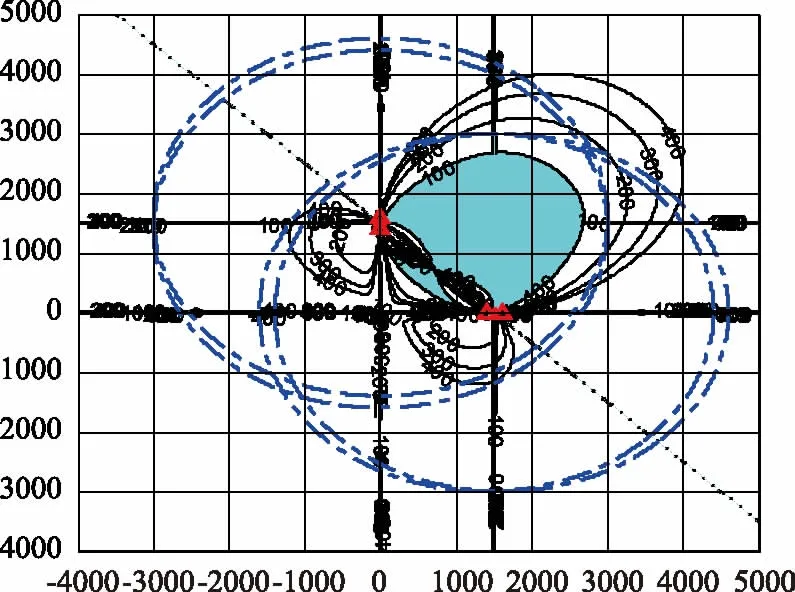
图12 典型误差条件下CODAR阵定位精度分布

由上述分析，可知：各误差源导致的测角误差在空间分布中存在变化，使得CODAR阵的定位精度空间分布，从测角误差为定值时的沿CODAR对中心连线对称分布(图8)，变为单侧分布，分布在CODAR对中心垂线相交的一侧(图12)。表明CODAR阵定位具有一定的方向性。探测误差增大，使得CODAR阵定位精度较高的区域向CODAR对子中心连线收缩，分布范围减小。

3.2 布阵误差对定位精度的影响

为简化讨论，定义CODAR对的布阵误差如图13所示[2]。 仅考虑CODAR对子在布阵方向上偏移误差，暂不考虑CODAR对子自身旋转所带来的误差。

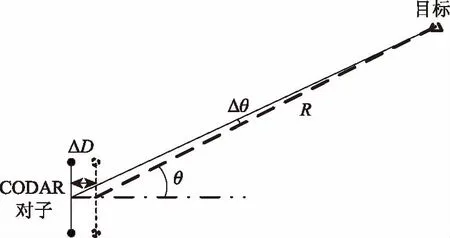
图13 CODAR阵布阵误差

图中，CODAR阵布阵误差，ΔD引起的角度误差，等效于ΔD对目标所形成的张角。由几何关系，有：

Δθ≈ΔD/R

(8)

式中，ΔD为CODAR阵的布阵误差，R为CODAR对子中心与目标间距离，Δθ为角度误差。

假设CODAR对中心点坐标1(0,1500);中心点坐标2(1500,0)(单位m)。浮标作用距离3000m。各误差源的典型值为：时延误差Δt=1ms；水中声速误差Δc=45m/s；浮标对间距误差Δd=5m。当布阵误差ΔD=100m时，定位精度如图14所示。

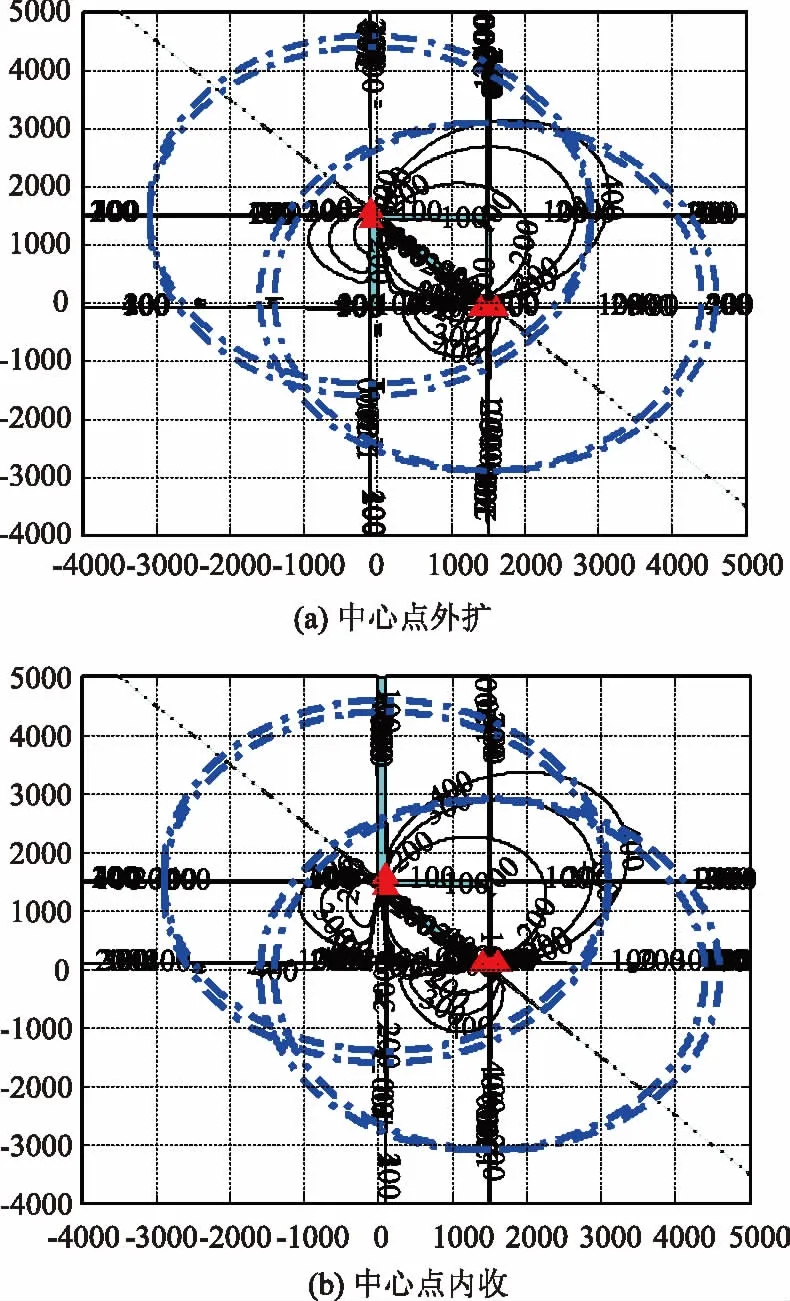
图14 布阵误差ΔD=100 m，CODAR阵定位精度分布

图14中，(a)、(b)分别为因布阵误差使CODAR对中心点外扩、内收时的定位精度分布。图中可看出，由于引入了布阵误差，CODAR阵的定位精度下降，特定精度区域的分布范围缩小。对相同的布阵误差，中心点内收的布阵，定位精度分布较优，如图14(b)所示。

布阵误差大小对定位精度分布影响如图15所示。图中阴影部分区域定位精度为100m。

由图15，随着布阵误差的增大，CODAR阵定位精度高的区域向CODAR对子中心连线收缩，分布区域缩小。

3.3 布阵间距对定位精度的影响

布阵间距即CODAR对中心连线的距离，其大小对CODAR阵的定位精度分布也有影响。

假设浮标作用距离3000m。时延误差Δt=1ms；水中声速误差Δc=45m/s；浮标对间距误差Δd=5m；布阵误差ΔD=100m时，CODAR对间距大小对定位精度分布的影响如图16所示。

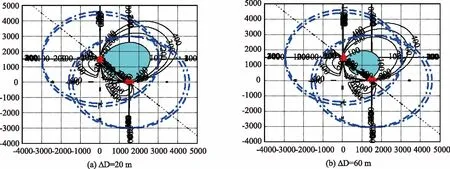
图15 布阵误差对CODAR阵定位精度分布影响

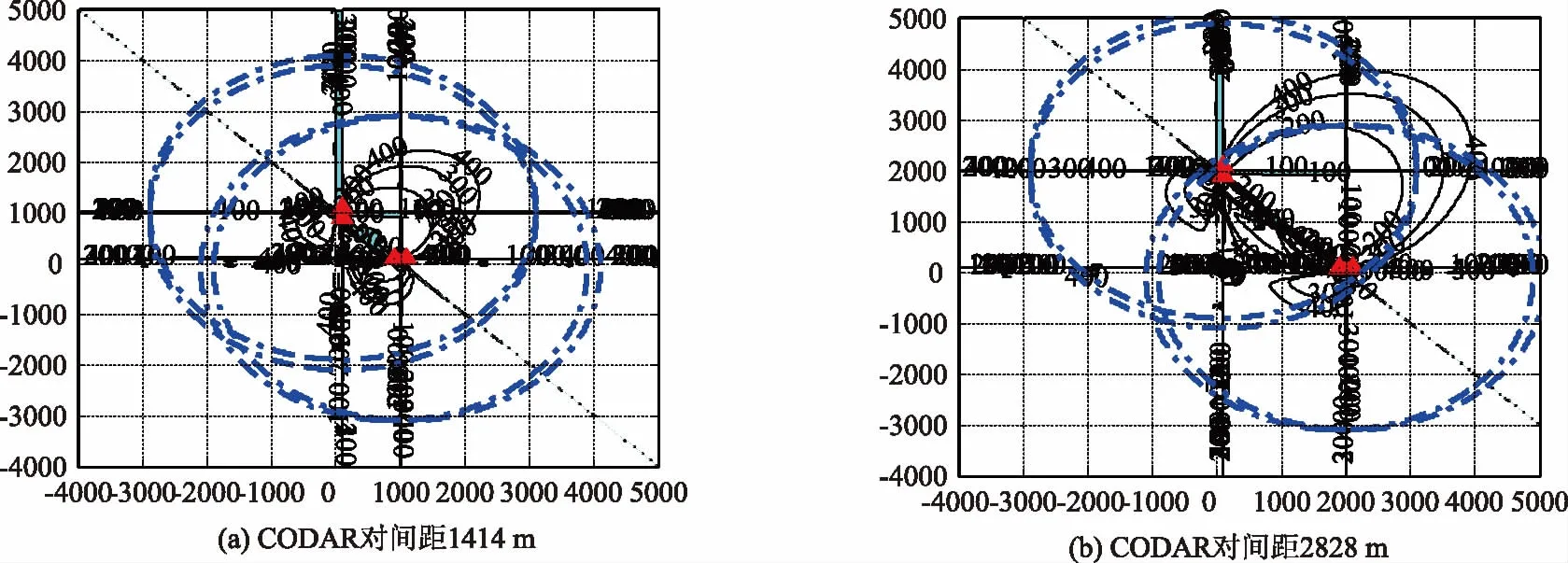
图16 CODAR对间距对定位精度分布影响

由图16，随着CODAR对子的布阵间距的扩大，定位精度较高的区域沿对子中心连线的垂直方向向外扩张，分布区域增大。但布阵间距增大，将使CODAR对子作用距离圆重叠区域减小，即CODAR阵的作用区域面积减小，导致浮标使用效率降低。实际应用中，应在布阵间距与浮标使用效率间折中考虑。

4 结 论

本文采用基于几何精度衰减因子(GDOP)的定位精度模型，分析CODAR阵探测过程中各误差源对定位精度分布的影响。CODAR阵定位精度分布与CODAR对子的测角误差、CODAR阵布阵误差及布阵间距有关。各误差源越大，定位精度较高的区域分布范围越小；布阵间距增大，可增大定位精度较高的区域分布范围，但同时会减小CODAR阵的作用区域面积。在工程应用中，可通过控制浮标对间距误差、布阵误差，及调整布阵间距的方式，使CODAR阵的定位精度更高，分布更为合理，更有利于定位目标。