闭口钢箱梁悬索桥涡振多尺度模型风洞试验
董浩天 葛耀君杨詠昕
(同济大学桥梁工程系,上海 200092)
0 引 言
大跨度扁平钢箱梁悬索桥的钝体气动外形、低阻尼比和低结构频率等特征使涡激振动较易发生[1]。涡振虽不像颤振、驰振和静风失稳等易引发结构破坏,但这种限幅振动对行车安全[2]、行人舒适[3]和结构耐久都有不利影响。我国规范[4]对公路桥梁涡振幅值上限做出了规定。
模型风洞试验是研究桥梁涡振的主要手段,包括节段模型风洞试验[5]、气弹模型风洞试验和测压模型风洞试验等。传统上,涡振研究中的尺度效应指节段模型风洞试验的缩尺效应[6],并主要表现为不同缩尺比下的雷诺数效应。Raghavan[7]试验分析了圆柱涡振随雷诺数的变化。鲜荣[8]比较了1∶50和1∶20扁平钢箱梁节段模型涡振试验,发现当雷诺数增大时斯托罗哈数和涡振振幅随之减小。熊龙[9]研究了雷诺数对钢箱梁涡振的影响。近年来,桥梁风致振动的多尺度研究方法为扁平钢箱梁悬索桥涡振研究指出了新的思路。多尺度方法包含不同尺度节段模型风洞试验、气弹模型风洞试验等试验手段以及数值模拟和现场实测验证等[10]。其中二维节段同三维全桥相比,其涡振现象既有相似特征也有显著差异。一方面,Ehsan和Scanlan[11]指出涡振中涡激力相比自激力是小量,而自激力在涡振发生时的跨向相关性很强;朱乐东[12]进一步研究了涡激力的跨向相关性,并提出节段与全桥涡振振幅换算关系;可见节段同全桥、实桥的涡振现象是可以比较的。另一方面,全桥气弹模型相对于节段模型可以模拟更多高阶振动模态[13],并再现构件之间的振动耦合。
然而,目前悬索桥涡振的多尺度试验研究仍较少,尤其是全桥气弹模型风洞试验仍被认为较难再现悬索桥涡振。目前在全桥风洞试验中发现的涡振多为结构刚度和模型风速比较大的500 m以下跨度斜拉桥[14],梁桥[15]和拱桥[16]等;而大跨度悬索桥的全桥模型结构基频低,风速比很小,涡振的再现较为困难。Zhou[17]用弹性支撑连续梁桥全桥模型等效模拟悬索桥,在风洞试验中再现了涡振现象;但等效试验未能模拟主缆、桥塔等构件的气动力。可见,多尺度方法在悬索桥涡振研究的应用,以及悬索桥全桥气弹模型风洞试验中是否会出现涡振现象都有待进一步探索。
本文采用多尺度风洞试验的方法,通过1∶60和1∶20两种不同尺度节段模型风洞试验,以及1∶122全桥气弹模型风洞试验,研究了大跨度扁平钢箱梁悬索桥的涡振现象。
1 模型涡振风洞试验
1.1 风洞试验概况
风洞试验以一座双塔三跨悬索桥为背景,跨径布置为:264 + 926 + 357 m;中跨双主缆矢高104.5 m,单根主缆净面积0.17 m2,如图1所示。加劲梁为闭口扁平钢箱梁,高3 m、宽30 m;桥面上有五道栏杆,底板有两道检修车轨道,如图2所示。利用ANSYSTM三维有限元模型动力特性分析,得到实桥第一阶对称竖弯振型的频率fb=0.125 Hz,第一阶对称扭转振型的频率ft= 0.390 Hz。风洞试验在同济大学土木工程防灾国家重点试验室TJ-2和TJ-3风洞完成,包含1∶60小尺度、1∶20大尺度节段模型和1∶122全桥气弹模型三组风洞试验。试验均在均匀流中进行,主要的试验参数见表1,雷诺数定义雷诺数Re定义为
(1)
式中:U为加劲梁高度来流风速;h为加劲梁梁高;ν为空气的运动黏度。
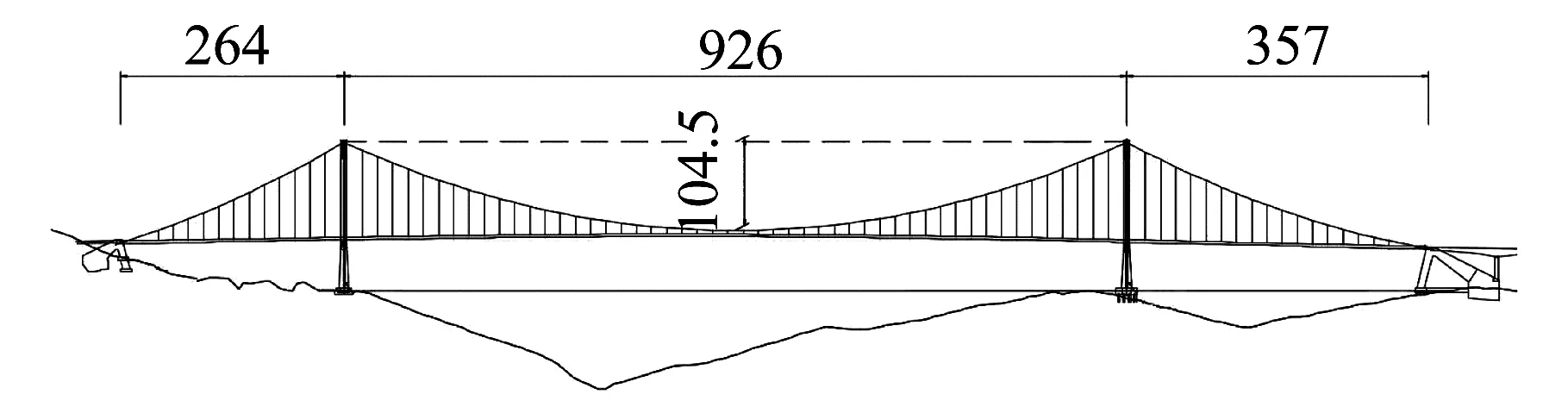
图1 悬索桥跨径布置 (m)Fig.1 Span arrangement (m)

图2 闭口钢箱梁断面布置 (m)Fig.2 Cross section of the closed steel box girder (m)
表1风洞试验主要参数对比
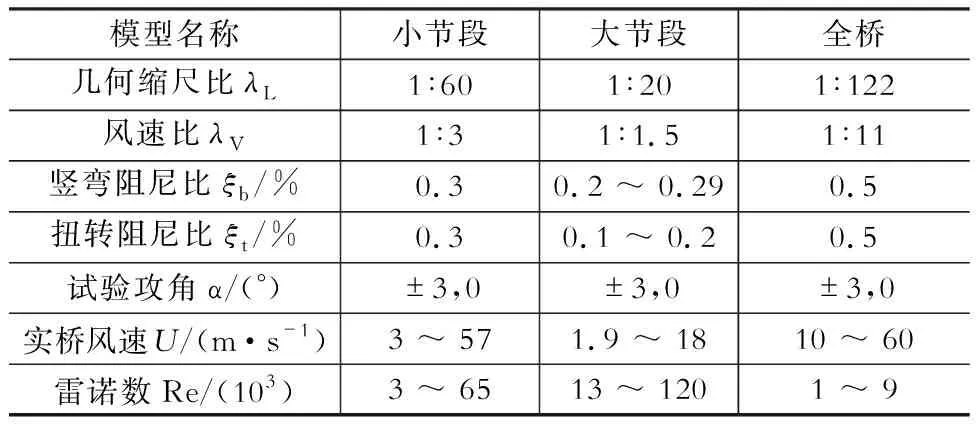
Table 1Comparison of main parameters of wind tunnel test
1.2 节段模型涡振风洞试验
1∶60小尺度节段模型涡振试验和1∶20大尺度节段模型涡振试验分别在TJ-2和TJ-3边界层风洞进行,试验系统如图3所示。TJ-2风洞高2.5 m,宽3.0 m,长15 m;可调风速1.0 m/s至68 m/s;试验段由两面挡墙围成,在上游方向为流线型断面,在中间试验段则平行于来流方向,间距1.8 m。TJ-3风洞高2 m,宽15m,长14 m;可调风速1.0 m/s至17.6 m/s;两面挡墙同TJ-2相似,挡墙之间在试验段的宽度为3.6 m。小节段模型长1.74 m,宽0.5 m,高0.05 m;大节段模型长3.6 m,宽1.5 m,高0.15 m。节段模型均通过弹簧和悬臂系统与挡墙连接,可同时一阶对称竖弯和一阶对称扭转频率。四个激光位移计安装在挡墙外侧悬臂,量程(13±5) cm,通过DASP数据动态信号采集和测试分析系统、HP35670A信号分析仪、模拟式信号采样板和YE5688电荷放大器同步测量模型的运动时程。

图3 节段模型涡振风洞试验系统Fig.3 Section model VIV wind tunnel tests
根据朱乐东[12]的研究,考虑从节段模型到实桥的振幅修正,可偏保守的取修正系数4/π,得到修正后的实桥竖弯和扭转涡振振幅yfull、αfull同节段模型涡振振幅测量值ysectional、αsectiona的关系:
(2)
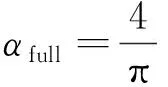
(3)
则两种尺度的节段模型在±3°和0°风攻角的实桥修正竖弯和扭转涡振振幅-风速曲线如图4所示,涡振锁定风速区间和振幅如表2所示。小尺度节段模型在+3°和-3°风攻角下均存在实桥风速10 m/s附近的扭转涡振现象,振幅分别为0.35°和0.14°;并没有发生竖弯涡振现象。另一方面,大尺度节段模型试验中除了在-3°风攻角下实桥风速10 m/s附近观测到振幅0.18°的扭转涡振之外,在-3°风攻角下实桥风速2 m/s附近还发生了振幅0.057 m的小幅竖弯涡振。
1.3 全桥气弹模型风洞试验
全桥气弹模型涡振风洞试验在TJ-3边界层风洞进行,三个攻角下的试验系统布置如图5所示。
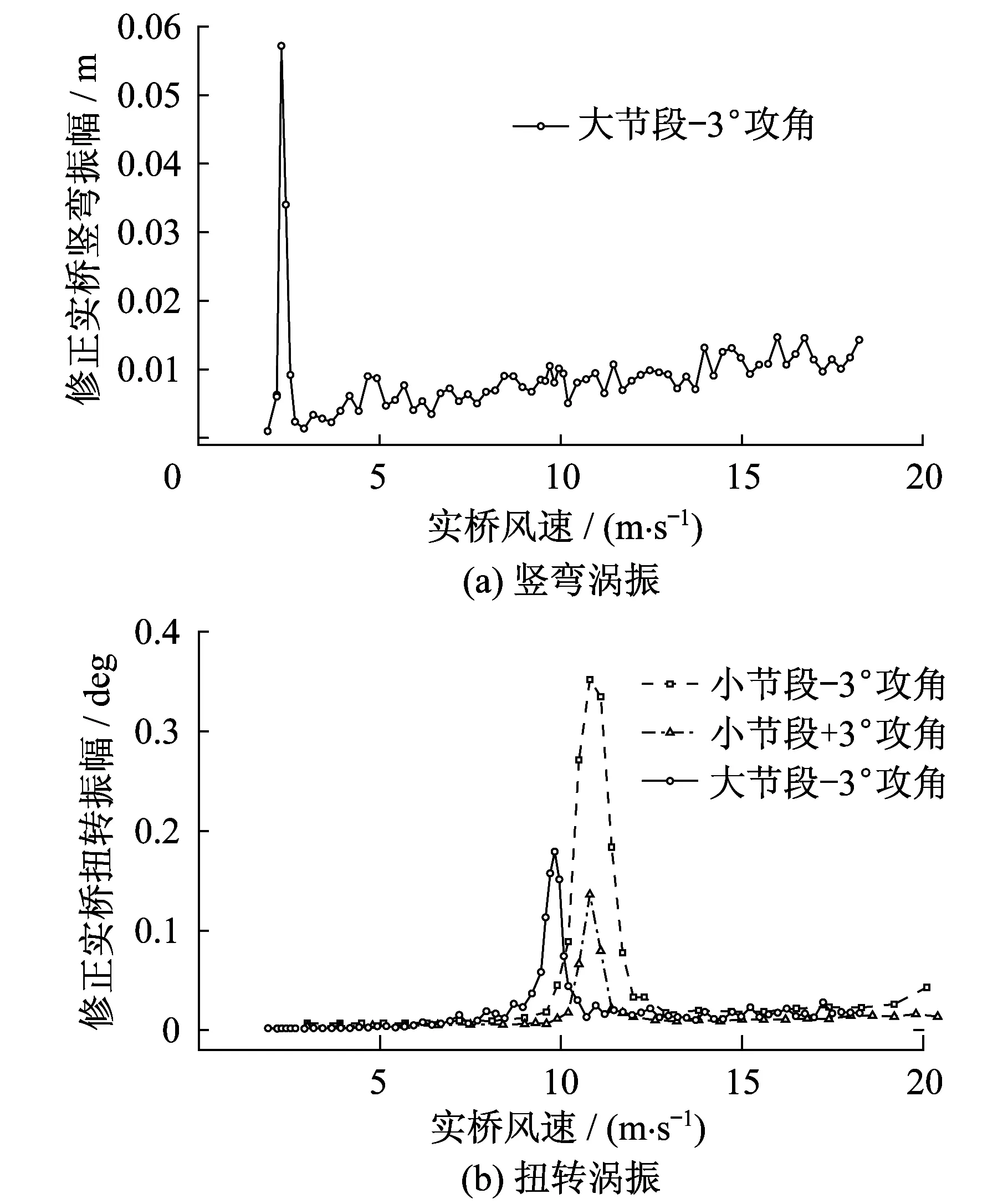
图4 节段模型涡振试验振幅-风速曲线Fig.4 Modified VIV bending and torsional amplitude with wind speed of two sectional models
表2两种尺度节段模型涡振试验结果
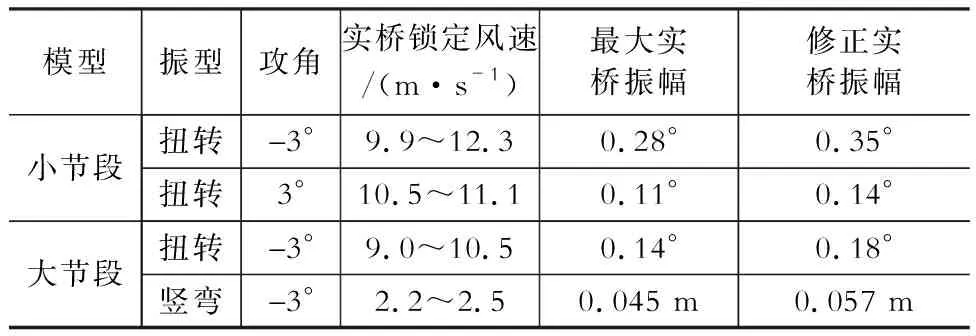
Table 2Results of sectional model VIV tests
+3°和-3°风攻角通过斜坡板实现,坡板设置满足阻塞率要求。气弹模型采用钢芯梁模拟加劲梁和主塔的刚度;钢丝模拟主缆刚度;塑料模拟加劲梁和桥塔的气动外形;铜块同钢丝一起模拟主缆气动力和质量;配重模拟加劲梁和主缆质量。流场风速标定采用眼镜蛇三维脉动风速测量仪(Cobra Probe),主要布置在气弹模型中心上游加劲梁高度处;参考风速测量采用皮托管和电子微压计,布置在桥轴线的延长线上,测点高度与桥面高度一致。位移响应测量采用激光位移计,在加劲梁中跨的跨中、左四分点、右四分点以及右侧边跨跨中分别布置3个位移计,测量竖向、侧向和扭转位移;在桥塔塔顶设置1个顺风向(垂直桥轴方向)位移计和1个横风向(桥轴方向)位移计;在下游主缆的跨中和右四分点分布设置1顺风向位移计。共布置激光位移计16个,并同步采样。

图5 全桥气弹模型涡振风洞试验系统Fig.5 Aeroelastic model VIV wind tunnel test
全桥气弹模型的动力特性测试检验了一阶正、反对称侧弯,一、二阶正、反对称竖弯和一阶正、反对称扭转等振型的频率和运动状态,如表3所示,同ANSYSTM三维有限元模型动力特性计算的理论频率的误差均在5%以内,验证了全桥气弹模型对多阶结构振动模态模拟的准确性。
表3全桥气弹模型动力特性测试
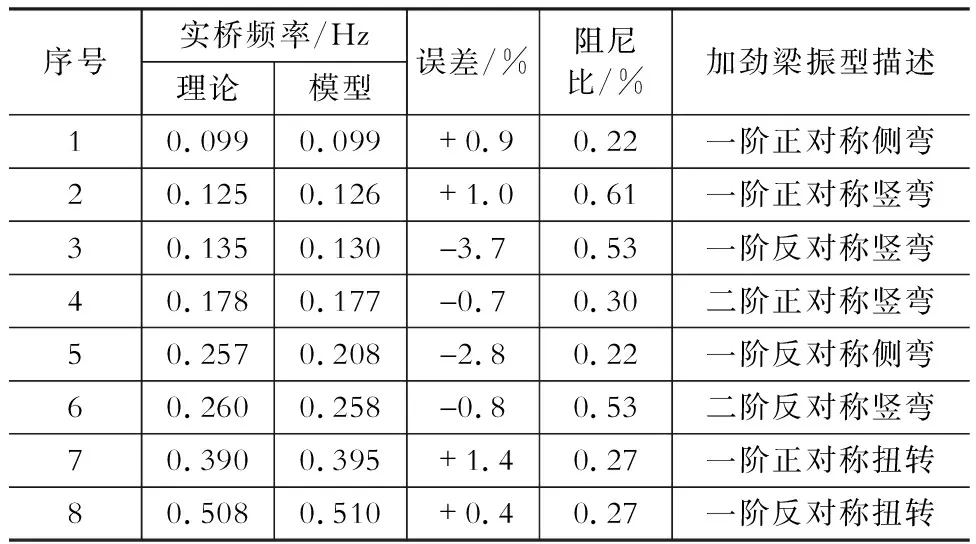
Table 3Measurements of dynamic properties of aeroelastic model
在全桥气弹模型涡振试验中发现了-3°风攻角、39~41 m/s高实桥风速区间下加劲梁扭转(包括中跨和边跨)、桥塔弯曲和主缆位移共同参与的涡振现象,如图6所示。具体来说,在-3°攻角实桥39~41 m/s,加劲梁的中跨跨中、左四分点、右四分点和边跨跨中均发生扭转振动,同时右桥塔观测到顺风向和横风向振动。而对于主缆,在+3°和-3°均在实桥35~45 m/s发生一阶正对称横风向涡振。从振幅上看,中跨跨中振幅大于中跨左右四分点振幅大于边跨跨中振幅,表现出正对称扭转的振型。但由于两边跨跨长不一致,悬索桥不是严格对称的,中跨左右四分点振幅有一些差异。从风速锁定区间来看,主缆的涡振区间宽于加劲梁和桥塔。
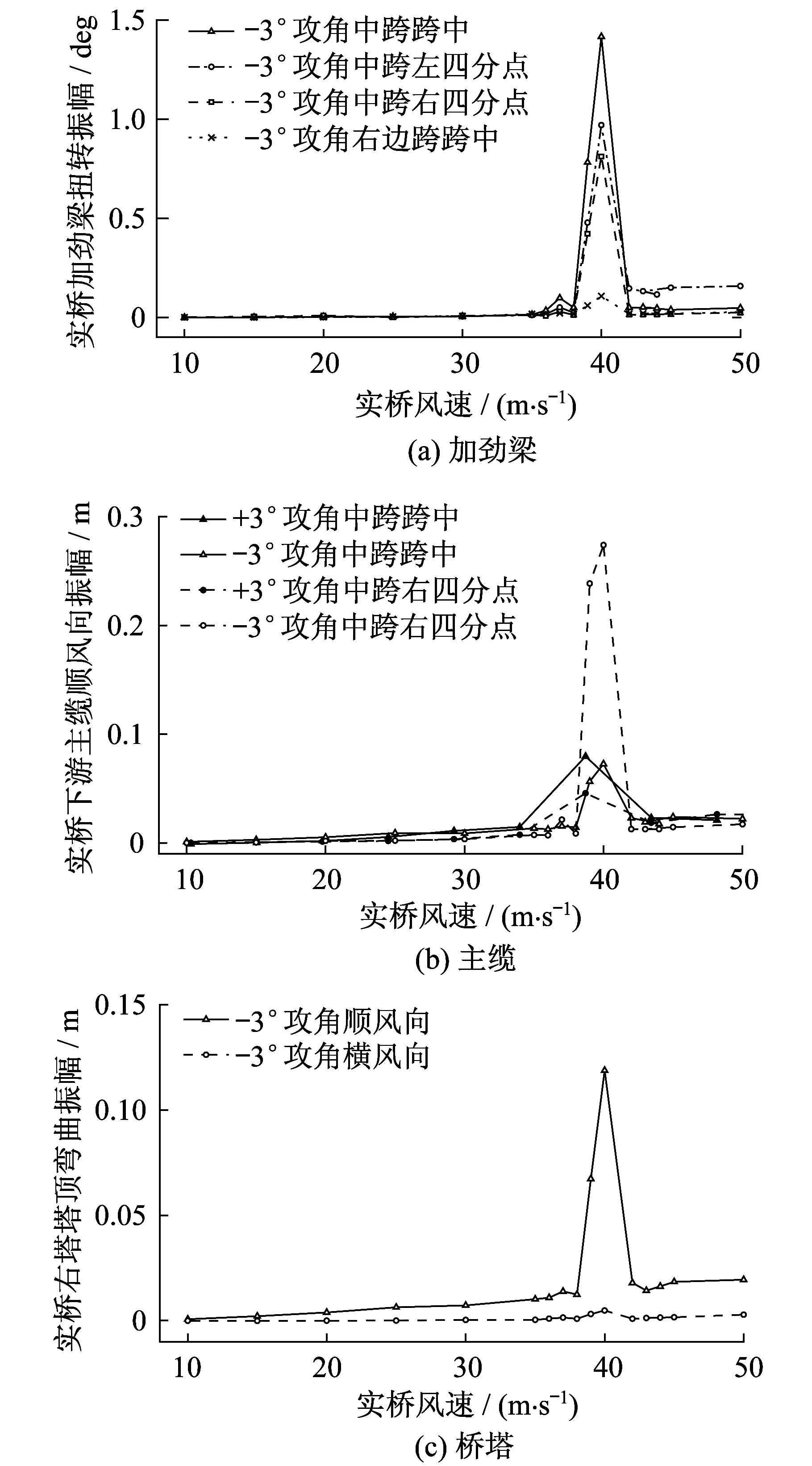
图6 全桥气弹模型实桥涡振振幅-风速关系Fig.6 VIV amplitude-wind speed relationship
2 涡振的多尺度效应
2.1 缩尺效应
三个尺度的涡振模型风洞试验在涡振发生的风攻角、锁定风速区间、振幅和频率方面都存在一定的差异。根据式(3),全桥、小节段、大节段模型扭转涡振风速的的雷诺数Re分别为6 000、12 000、65 000。可见,在小、大尺度节段模型的扭转涡振表现了雷诺数效应的影响,即随着Re从12 000增加到65 000,修正实桥扭转振幅从0.35°减小到0.18°,发振实桥风速从9.9 m/s降低到9.0 m/s;熊龙[9]对扁平钢箱梁节段模型的竖弯涡振也得到了相似的结论,即在雷诺数从50 000增加到300 000时,竖弯涡振实桥振幅从0.47 m缩小到0.10 m。总的来说,随着雷诺数增加,节段模型试验中的涡振发振速度降低,振幅变小[8]。
除了雷诺数效应,涡振现象在不同尺度试验中是否能够重复同试验风速区间的选取、测试风速的密集程度、风洞的风速稳定性和模型制作精度等有关;如大节段试验中的竖弯涡振没有在小节段试验中再现,而全桥试验也由于风速比的原因没能再现低风速涡振。
2.2 全桥涡振的机理分析
首先,由于材料弹性模量的限制,全桥试验中采用钢丝模拟主缆轴向刚度,分段圆柱铜块模拟主缆质量和总迎风面积;而主缆气动外形未严格缩尺。同全桥模型的几何缩尺比λL=1∶122相比,铜块直径缩尺比为λLb=1∶83。尽管主缆重力和静气动力满足缩尺要求,但分段圆柱绕流受到雷诺数和不连续几何外形影响较大,主缆的涡激力和自激力未等比例缩尺。因此,全桥试验中的主缆一阶正对称涡振难以同实桥直接比较。
图7给出了-3°攻角全桥试验在涡振发生时,加劲梁中跨跨中扭转、右桥塔塔顶顺风向位移和下游主缆跨中顺风向位移的一段同步振动时程。图8进一步给出对应的频谱图。可见在0.36 Hz左右所有构件都有一个卓越频率。在此卓越频率上,主缆顺风位移、加劲梁扭转和塔顶顺风向位移同步运动,但主缆的运动同后两者存在相位差;在试验中也观察到两根主缆的低频相互运动,即图8在0.1 Hz左右的峰值,这是导致相位差的主要原因。又如图6所示,主缆一阶正对称弯曲的起振风速早于加劲梁和桥塔,而锁定风速区间35~45 m/s明显宽于后两者的39~41 m/s范围。而涡振时主缆、加劲梁和桥塔共振频率f=0.36 Hz,小于有限元分析和桥模型动力特性测试得到的加劲梁一阶正对称扭转实桥基频ft=0.390 Hz与ft=0.395 Hz。合理的解释是,全桥模型主缆自身一阶正对称振动的频率在0.36 Hz附近,并在实桥35 m/s起振;当风速继续增加后,加劲梁的气动刚度下降,在风速39 m/s时实际的结构基频从0.39 Hz下降到0.36 Hz附近,主缆涡振引发了主缆同加劲梁的共振,并最终表现为主缆、加劲梁、桥塔三者共振;当风速继续增加到41 m/s以上,气动刚度进一步下降,结构基频下降到小于0.36 Hz,加劲梁的共振结束。
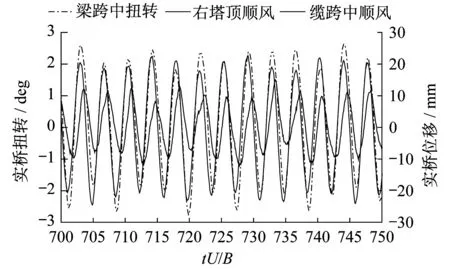
图7 全桥气弹模型-3°攻角涡振运动时程Fig.7 Model coupling VIV displacement history
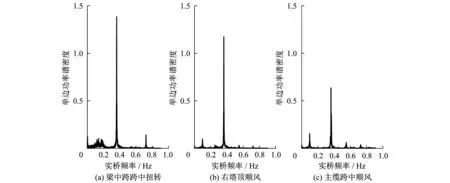
图8 全桥气弹模型-3°攻角涡振模型频谱Fig.8 Power spectral density of model VIV
3 结 论
通过多尺度风洞试验方法研究了闭口钢箱梁悬索桥涡振现象。在节段模型涡振试验中,模型尺度增大后风速锁定区间变窄并提前,涡振振幅降低,体现出雷诺数效应的影响。对于扁平钢箱梁悬索桥涡振的试验研究,特别对于低风速涡振现象,应尽量采用较大尺度的节段模型;而全桥试验中难以再现低风速涡振。在全桥气弹模型风洞试验中发现了由主缆涡振激发的,高风速下加劲梁气动刚度下降引起的,加劲梁、桥塔、主缆三者共振的涡振现象,在振动模式、涡振风速锁定区间和振幅上都同节段模型试验有较大差异。但由于全桥试验中主缆雷诺数和气动外形未严格缩尺,难以同节段模型试验直接对比;这种多构件参与的涡振现象是否在实桥中存在还有待进一步研究。

