某工程无楼板支承的楼梯间剪力墙稳定性分析
陈 柯 郏建磊 杨健兵 张 弛 管前黔
(成都基准方中建筑设计有限公司,成都 610011)
0 引 言
高层住宅设计中,采用《高层建筑混凝土结构技术规程》(以下简称《高规》)附录D验算楼梯间处剪力墙稳定性时,经常会出现稳定性验算不过的情况。特别是当楼梯间设置在外侧,这时楼梯间剪力墙没有楼层板的支撑作用,按照《高规》附录D的要求,该剪力墙的计算高度为全楼通高,这样剪力墙稳定性验算肯定是不满足的。但如果考虑了梯段斜板对于剪力墙的支撑作用,剪力墙的计算高度为上下梯段的距离,墙体稳定性得到大大改善。本文通过有限元方法验证了梯板对剪力墙的支撑作用,在计算剪力墙稳定性时,可以将梯段斜板看作墙体的支撑点进行稳定性计算。同时可以发现,即使考虑了较大的初始几何缺陷,剪力墙仍然先发生强度破坏,混凝土被压溃,但并未发生失稳。
1 理论基础
1.1 《高规》关于剪力墙稳定性的规定
根据国内研究成果并与德国《混凝土与钢筋混凝土结构设计和施工规范》(DIN1045)的比较表明,对不同支承条件弹性墙肢的临界荷载,可表达为统一形式:
(1)
式中:计算长度l0取为βh,β为计算长度系数,可根据墙肢的支承条件确定;h为层高。

1.2 特征值屈曲分析
特征值屈曲是以刚度矩阵的特征值为研究对象,特征值是理想的材料线性和几何线性结构理论屈曲强度,采用经典欧拉压杆失稳法分析方法进行分析,在有限元中采用的是特征值求解器。
特征值屈曲求解原理是,通过求解结构刚度矩阵特征值λ,再用特征值λ乘以所加荷载Q,得到屈曲临界载荷。在特征值求解器中,定义在特征值屈曲预测分析步中递增载荷Q的幅值大小不重要,因为Q会被相应的载荷乘数λ缩放。

针对线性特征值屈曲分析,特征值求解器一般自带两种特征值求解方法:卢卡斯(Lanczos)和子空间(Subspace)迭代。
当一个多自由度系统需要求解许多特征模态时,Lanczos方法通常比较快,但当少于20个特征模态需要求解时,Subspace方法更快。
1.3 非线性屈曲分析(弧长法)
特征值分析是一种材料线性和几何线性结构的理论解。但是由于焊接应力、温度应力、安装误差、加工误差等因素的影响,现实中的结构都会存在一定的初始缺陷,其屈曲临界载荷与特征值理论解肯定存在一定的差别。另外,由特征值屈曲分析是材料线性和几何线性的,它不可以考虑构件的材料非线性和几何非线性,如果在发生屈曲之前部分构件进入塑性状态,那么特征值屈曲也是无法模拟的。所以必须利用非线性有限元理论对结构进行考虑初始几何缺陷、材料弹塑性等实际因素的稳定性分析。
目前应用较多的是利用弧长法对结构进行“荷载-位移”全过程跟踪技术,来达到计算结构整体稳定承载力的目的。使用弧长法,能够建立不稳定响应段的静力平衡状态,此方法适用于载荷为比例加载,即载荷大小由一个标量参数控制。即便是复杂的不稳定响应,应用此方法也能求解。
弧长法本质上就是静力问题求解,通过附加一个约束方程,就可以应用叠代方法求解收敛点,但是,如果叠代方向判断错误,将导致所谓的跟踪返回现象,因此叠代方向的判别法对于弧长算法非常重要,其关键点就是对每一增量步的最初叠代方向的判别。
图1描述了弧长法叠代非线性求解的收敛过程。其计算的具体过程如下:
(1) 以增量形式逐渐施加载荷。
(2) 在每一载荷增量中完成平衡叠代来使增量求解达到平衡。
(3) 求解平衡方程:
[KT]{Δu}=λ{Fn}-{Fnr}
(2)
式中:[KT]为切线刚度矩阵;{Δu}为位移增量;{Fn}为外部载荷向量;{Fnr}为内部力向量;λ(-1<λ<1)为载荷因子。
其中,位移增量{Δu}与载荷因子λ通过弧长半径l相联系,其约束方程为:
(3)
(4) 进行叠代,直到λ{Fn}-{Fnr}在允许的范围内。
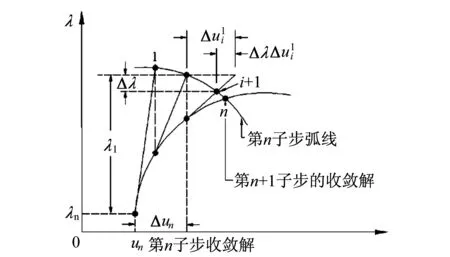
图1 弧长法的收敛过程Fig.1 Convergence of riks method
2 工程概况
某超限高层住宅,底层层高为5.6 m,全楼高度146.75 m。楼梯间设置在外侧,楼梯间外侧剪力墙无楼层板的支承作用,按照《高规》附录D,稳定性计算高度为全楼通高146.75 m。墙体两边开洞,底层墙体墙厚250 mm,墙体轴力设计值为2 457.8 kN/m2,如图2所示。

图2 一层楼梯平面布置图Fig.2 First floor plan of stairs
采用《高规》附录D计算该剪力墙的稳定性。当不考虑梯段斜板对墙体的支撑作用时,剪力墙无支撑高度为全楼通高,不满足规范要求。当考虑梯段斜板对墙体的支撑作用时,剪力墙无支撑高度为2.8 m,qcr2=7 175 kN/m2>2 457.8 kN/m2满足规范要求。
表1《高规》的墙体稳定性验算结果

Table 1Wall stability check results in Technical Specification for Concrete Structures of Tall Building
3 墙体的简化模型分析
将该楼梯间简化为四边简支板:
1) 简化模型一:墙高146.75 m;
2) 简化模型二:墙高2.8 m。
模型一和模型二:宽度为7.6 mn,墙厚250 mm,混凝土C60,E=36×109N/m2,边界条件为四边简支。
首先根据弹性薄板稳定性理论公式求解。
(4)
(5)
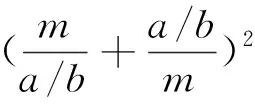
(6)
(7)
式中:b为板的宽度;k为屈曲系数;D为单位宽度板的弯曲刚度;m为半波数(屈曲形状)。
理论公式计算结果:
1) 模型一:k=4,m=17,Ncr=32 040 kN/m;
2) 模型二:k=9.949,m=1,Ncr=76 015 kN/m。
在求解过程中可以发现:对于四边简支板,当墙高大于墙宽时,失稳临界荷载与墙高无关,与墙宽有关,即146.75 m高的墙与7.6 m高的墙计算结果是相同的。原因是,对于四边简支板来说,除有上下水平位移约束外,还有左右水平位移约束,当墙体的高度与宽度比值较小时,左右水平支座对板的约束较小,随着高度与宽度比值不断加大,左右水平支座对板的约束不断加大,屈曲系数k不断减小。当高度与宽度相等时,屈曲系数k到达最小值4。当高度比宽度大时,屈曲系数约等于4不再减小,如图3所示。

图3 屈曲系数k随h/b变化规律Fig.3 Variation of k with h/b
采用特征值屈曲方法和考虑初始缺陷的非线性屈曲方法对模型一和模型二进行数值求解。
采用大型通用有限元分析软件ABAQUS进行建模和计算。使用ABAQUS中的Lanczos特征值求解器进行特征值屈曲分析,使用ABAQUS/ Standard模块进行非线性屈曲分析。墙体采用壳单元S4R进行模拟。材料本构为弹性。
进行非线性屈曲分析时,需要先进行特征值屈曲分析,得到第一阶屈曲模态,再将第一阶屈曲模态做为非线性屈曲分析模型的初始缺陷,通过ABAQUS自带的非线性屈曲算法(Riks法)进行求解计算。
从屈曲模态可以看出:当墙高大于墙宽时,四边简支板由于左右两边支座的约束作用,屈曲模态是多个半波组成,如图4所示;当墙高小于墙宽时屈曲模态为一个半波,如图5所示。
解析解与数值解求解结果如表2和表3所示。

图4 简化模型一的一阶屈曲模态Fig.4 Frist order buckling mode of simplified model Ⅰ
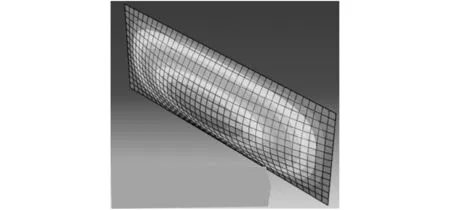
图5 简化模型二的一阶屈曲模态Fig.5 Frist order buckling mode of simplified model Ⅱ
表2解析解与数值解计算结果对比
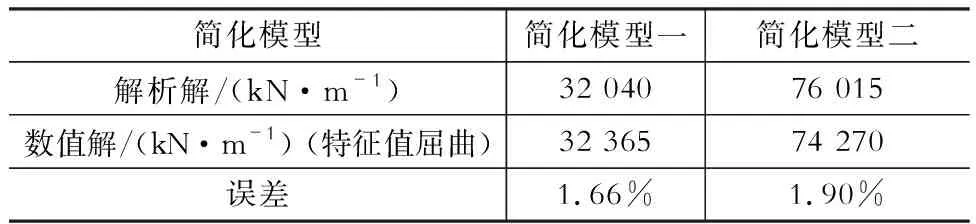
Table 2Comparison of analytical solution and numerical solution
表3简化模型计算结果汇总

Table 3Results of simplified model
注:数值解一采用特征值屈曲方法,数值解二采用非线性屈曲方法
由表2可以看出:解析解与数值解(特征值屈曲方法)结果基本一致,误差都在2%以内。说明数值解法是精确可靠的。
由表3可以看出:当考虑了梯段斜板的有利作用时(简化模型二)比不考虑梯段斜板的有利作用(简化模型一)的失稳临界荷载提高了大约2.3倍。
4 墙体的精细模型分析
墙体的精细模型同样采用ABAQUS软件进行建模和计算,墙体采用壳单元S4R进行模拟,材料本构为弹性。
按实际情况建立有限元模型:①模型一,没有梯段斜板的模型;②模型二,有梯段斜板的模型,如图6、图7所示。

图6 模型一(没有梯段斜板)Fig.6 Model Ⅰ without ladder board
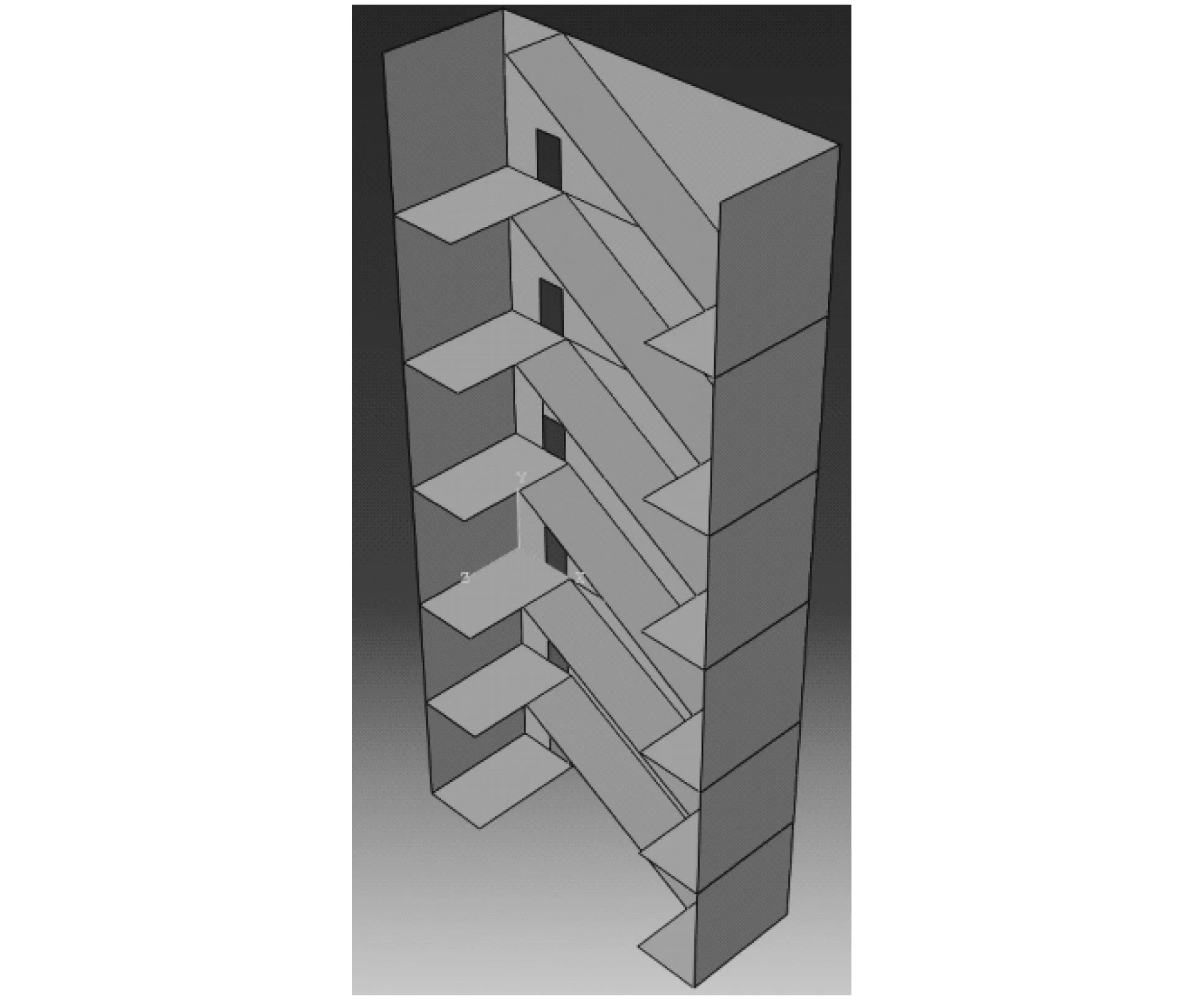
图7 模型二(有梯段斜板)Fig.7 Model Ⅱ with ladder board
可以发现在弹性分析中,模型二比模型一稳定性承载力提高了1倍左右,如表4所示。说明梯段斜板对墙体起到了支持作用,有效减小墙体的无支撑高度。
所以,计算剪力墙稳定性时,可以将梯段斜板看作墙体的支撑点进行稳定性计算。

图8 模型一的一阶屈曲模态Fig.8 Frist order buckling mode of model Ⅰ

图9 模型二的一阶屈曲模态Fig.9 Frist order buckling mode of model Ⅱ
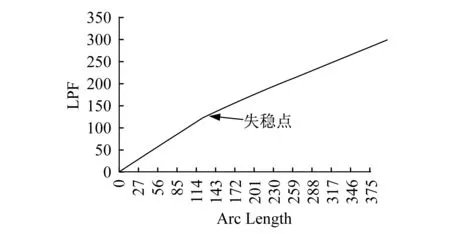
图10 模型一的非线性屈曲分析结果Fig.10 Nonlinear buckling analysis results for model Ⅰ
虽然楼梯间顶层无楼梯板,剪力墙无支撑长度会大于层高,对稳定性墙体稳定性不利,但顶层剪力墙轴力很小,一般能满足《高规》附录D的墙体稳定性要求。

图11 模型一的非线性屈曲分析结果Fig.11 Nonlinear buckling analysis results for model Ⅱ
表4有限元法的墙体稳定性计算结果

Table 4Finite element method results of wall stability
此外,通过有限元分析结果可以发现,该墙体并不是简单无侧边支撑剪力墙,墙体两边的深连梁对于剪力墙有一定的约束作用,这样对于墙体稳定性是有利的。再者,中间休息平台与墙体连接,对墙体也产生了一定的约束作用,对墙体稳定性也是有利的。而采用《高规》附录D的稳定性验算公式中,均未考虑这些有利影响。
对比简化模型的计算结果(表3)和精细化模型的计算结果(表4)可以发现,表3和表4中模型一的计算结果差3倍,模型二的计算结果差2.5倍。分析原因,可以发现简化模型和精细化模型在边界约束条件上是不同的。简化模型的边界条件为四边简支,而精细化模型由于墙体左右两边开洞,如图2所示,只是洞口上面的连梁部分对其进行约束,约束作用较弱。即在建立精细化模型时该片墙体上下边采用简支,墙体左右边是由连梁对其进行约束的。相比理想简支边界条件,连梁对墙体的约束要小很多,约束条件越弱计算结果越小。
5 采用弹塑性有限元模型验证墙体稳定性
将模型一和模型二的混凝土和钢筋材料设为弹塑性本构模型进行有限元分析,验证该片墙体稳定性。
墙体的弹塑性模型采用ABAQUS软件进行建模和计算,墙体采用壳单元S4R进行模拟,钢筋采用ABAQUS壳单元自带的钢筋层进行输入,在该方法中钢筋以壳元中积分点形式存在的。混凝土本构和钢筋本构均为弹塑性本构。
混凝土采用混凝土损伤塑性本构(Concrete Damaged Plasticity),本构模型的参数采用《混规》C60的相关参数,如图12、图13所示。钢筋采用理想弹塑性模型,屈服强度360 MPa。剪力墙水平和竖向分布筋均为10@130。

图12 混凝土受压应力-应变曲线Fig.12 Stress-strain curve of concrete under compression

图13 混凝土受拉应力-应变曲线Fig.13 Stress-strain curve of concrete under tension
模型初始几何缺陷采用5%一阶屈曲模态,如图14、图15所示,进行几何非线性分析。一阶屈曲模态由前面的特征值屈曲分析得到。
由计算结果可知,模型一和模型二在墙体轴力2 457.8 kN/m (墙体实际受到的轴力)作用下并没有发生失稳。继续加载到12 000 kN/m左右时,混凝土已经被压溃,从而丧失承载能力,此时并没有发生失稳破坏。此时的轴力12 000 kN/m远大于按《高规》计算的考虑梯板支撑作用剪力墙稳定性承载力7 175 kN/m。

图14 模型一的初始几何缺陷Fig.14 Initial geometric imperfection of modal Ⅰ

图15 模型二的初始几何缺陷Fig.15 Initial geometric imperfection of modal Ⅱ

图16非线性屈曲分析(弹塑性)分析结果Fig.16 Nonlinear buckling (elasto-plastic) analysis results
表5有限元法的墙体稳定性计算结果

Table 5Finite element method results of wall stability
6 针对墙体稳定性采取的加强措施
为了保证楼梯梯板对剪力墙起到有效的侧向支撑作用,墙体稳定性采取的加强措施:
(1) 平台板和斜梯板均增到150 mm厚;
(2) 斜梯板的分布钢筋为φ12@150锚入剪力墙中;
(3) 梯段斜板按照深梁进行配筋加强,如图17所示。
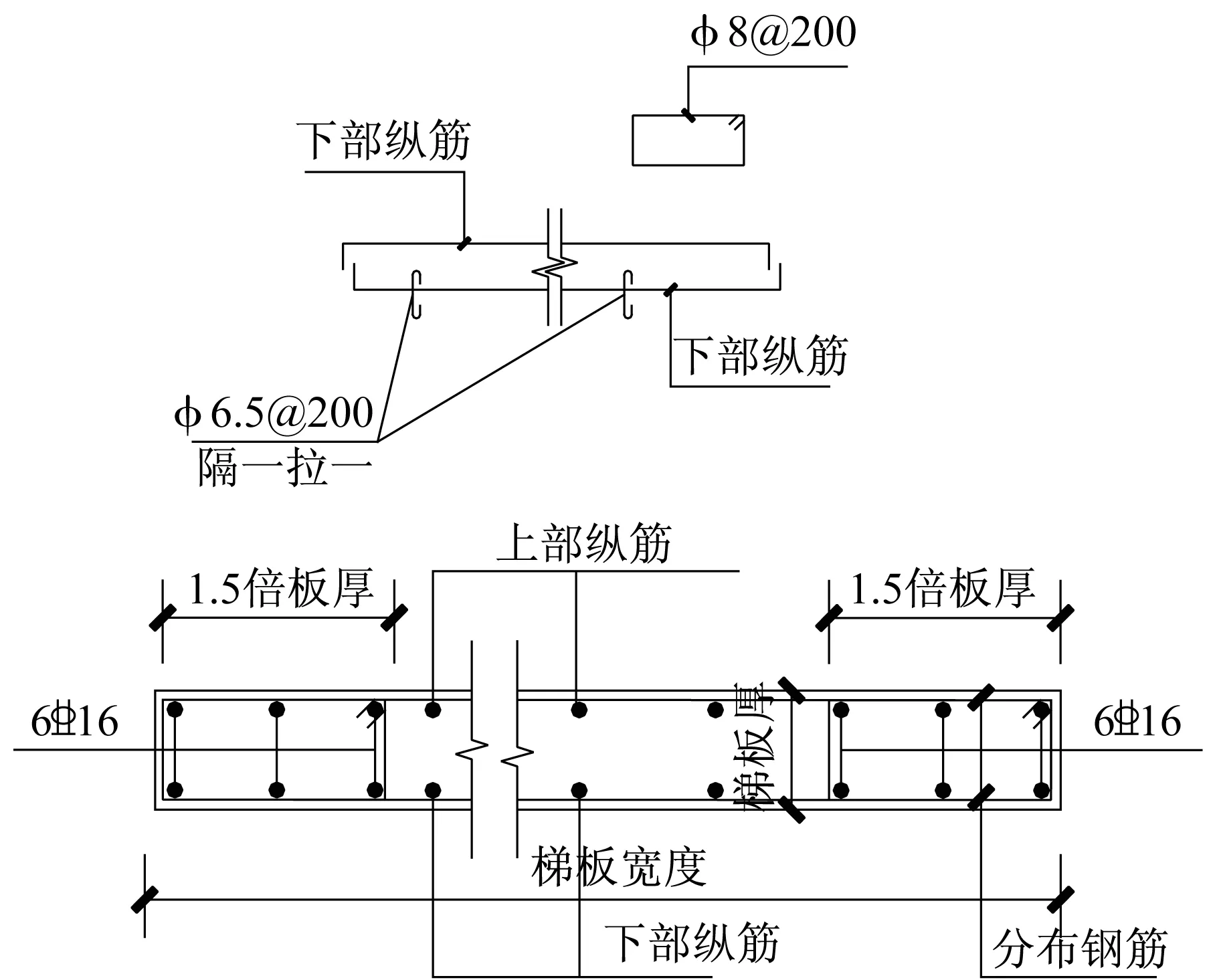
图17 梯段斜板的加强措施Fig.17 Strengthening measures of ladder board
7 结 论
通过前面的分析可以得到:
(1) 当墙体为四边支承时,墙高大于墙宽时,失稳临界荷载与墙高无关,由于左右两边支承的约束作用,屈曲模态是多个半波组成。
(2) 计算剪力墙稳定性时,可以将与墙体可靠连接的梯段斜板看作墙体的支撑点进行稳定性计算。
(3) 通过非线性稳定性分析(弹塑性)可知,结构先发生强度破坏,而并未发生失稳,此时的轴力远大于规范稳定性计算限值。
(4) 实际工程中对于因墙体高度较高而又无法增设侧向支撑的情况,除了增加墙厚的措施外,还可以通过本文分析方法验算其墙体稳定性。

