带传扭销的环形平面接触轴段扭转特性研究
夏凯,孙岩桦,卓明,赵世全
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;3.东方汽轮机有限公司,618000,四川德阳)
重型燃气轮机转子多采用盘式拉杆转子结构,由单个中心拉杆或多根周向拉杆将多级轮盘压紧而成,且轮盘间的接触为环形平面接触或圆弧端齿配合。环形平面接触界面由于传扭能力差,一般在接触环形平面间设有传扭销以增加接触界面的传扭能力,如M701F燃机转子。带传扭销的环形平面接触界面使转子产生结构上的不连续性,一定程度上削弱了接触界面所在轴段或转子的刚度,从而使得转子在传扭销承受扭矩阶段,转子的扭转动力学特性势必与连续转子有所不同。因此,有必要对带传扭销的环形平面接触轴段的扭转特性进行深入研究。
以往的研究中,学者们多关注于平面接触面的法向刚度和切向刚度,对带传扭销的环形平面接触轴段的扭转特性的研究一直未有报道。文献[1]针对平面接触表面提出了一种在微观层面处理非光滑接触表面的描述方法(GW模型),在弹性范围获得了刚性平面接触的微凸体数目、平面接触面积及载荷期望值与两平面间距离的关系式。文献[2]以GW模型为基础,从材料表面微观特征的分析入手,考虑了粗糙表面波纹度的影响,综合运用弹性接触理论和概率分析方法,在理论层面初步解决了拉杆转子接触刚度的计算问题。文献[3]基于加工表面的自仿射特征,以具有尺度独立性的分形维数和分形粗糙度作为粗糙表面的表征参数,提出了分形接触模型(MB模型)。文献[4]基于球体与平面的接触理论和MB模型,给出了具有尺度独立性的粗糙表面切向接触刚度的理论计算方法,进行了数值仿真分析,并通过实验定性验证了该方法在粗糙表面小压力范围内的正确性。传统的GW、MB等粗糙接触面刚度解析模型仅适用于接触面压力不大的情况,在解决复杂形体接触及大载荷作用下的接触问题存在一定的局限性[5]。文献[6]基于本构关系,提出了用于精确求解可变性球面与刚性平板弹塑性接触问题的有限元模型,采用该模型研究了纯弹性、弹塑性和纯塑性3种状态的演变历程。文献[7]采用有限元法研究了含有正弦形状微凸体的粗糙平面与刚性平面的接触问题,通过数值计算分析了完全接触时所需的平均压力,给出了能够近似预测弹性和弹塑性正弦接触表面平均分离量的拟合曲线。文献[8]通过有限元数值计算分析了具有分形特征的粗糙表面的接触面积和压力分布,研究了分形尺度的影响。文献[9]对球体与刚性平面的摩擦接触问题进行了有限元分析,研究了摩擦因数与法向力的关系。但是,上述有限元接触模型在尺寸上都远小于实际工程结构,不适用本文所讨论的重型燃气轮机盘间接触问题。
针对带传扭销的环形平面接触轴段,本文根据平面接触面的受力情况和传扭销的受力变形关系,建立了接触轴段扭转特性的理论模型。其次,通过三维有限元接触分析对理论模型进行了验证,并进一步提出了接触轴段的扭转变形双线性模型。最后,分析了两个线性段扭转刚度、线性转折点扭矩以及接触界面所能传递的最大扭矩等扭转特性随压应力、摩擦因数、传扭销个数和传扭销直径等参数的变化规律。
1 扭转特性的理论模型
1.1 带传扭销的环形平面接触轴段结构
图1为某重型燃气轮机压气机转子半剖面示意图。该压气机转子由多级轮盘通过数根周向均布拉杆拉紧装配而成,轮盘之间通过环形平面接触界面传递扭矩。此外,接触平面沿周向均匀分布若干骑缝传扭销,用以辅助传扭。带传扭销的环形平面接触轴段结构如图2所示,在环形接触平面上加工若干径向销槽,用于放置传扭销,安装时先将传扭销放置于销槽内,然后合上轮盘并拉紧拉杆。设计的目的在于:当作用在轴上的扭矩超过轮盘间环形接触面的摩擦传扭能力时,可以通过扭矩销来进一步承载扭矩。因此,两轮盘间轴段传递扭矩的过程可分为两个阶段:在外部扭矩较小时,轴向压紧的接触平面保持黏合,主要靠接触面之间的摩擦力传递扭矩;当外部扭矩增大到一定值时接触平面之间开始滑动,传扭销承载额外的扭矩。

图1 某燃气轮机压气机转子半剖面示意图
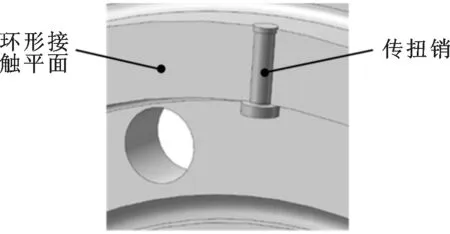
图2 带传扭销的环形平面接触界面结构
1.2 分析模型
虽然压气机转子存在多个轮盘,但结构特征都一样,不失一般性,可以取其中的一对接触轴段建立简化力学模型。由于传扭销直径较小,在分析环形接触平面摩擦传扭能力时,忽略传扭销的影响,两个在轴向压紧的等截面环形轴段,其中一端固定,另一端施加轴向的压紧力F和外部扭矩T,受力图如图3所示。由于受力过程中接触面上的应力是局部的,以两个轴段的接触平面为中心,取两端接触平面轴向距离各为0.5Lc的两横截面之间的轴段为研究对象,Lc的选取与盘间轴段的长度有关。

图3 环形平面接触受力图
环形接触平面滑动前所能传递的最大扭矩可表示为
(1)

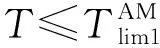
(2)
式中:G为材料剪切模量;Ip为极惯性矩。

(3)
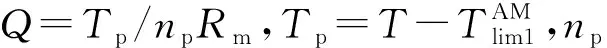
(4)
因此,带传扭销的环形平面接触轴段的扭转角θ可以写为
(5)
传扭销的传扭能力可以通过第三强度理论(最大切应力理论)进行估计,即传扭销最大切应力不大于屈服强度的一半,该强度条件为
(6)

(7)
式中:kμ为最大静摩擦因数与滑动摩擦因数之比。
上述的分析不考虑接触平面间的局部滑动,这和实际情况不同。实际的接触平面在外部扭矩较大时,会从外半径开始出现局部滑动,然后向内半径延伸,直至整个接触面发生滑动[12]。对于本文所研究环形接触面的整个传扭特性,这个过程是局部的,只在式(5)转折点附近一个很小的局部存在,这个局部变化对整体的扭转特性影响很小,可以忽略不计。因此,上述分析可以给出带传扭销环形平面接触轴段的扭转特性近似估计,这对带传扭销环形平面接触界面的设计非常重要。
2 理论模型的验证
采用有限元接触分析方法,进一步验证式(5)所得到的关于带传扭销环形平面接触轴段扭转特性理论模型的正确性。
2.1 有限元模型
带传扭销环形平面接触轴段具有周期循环对称性,为了简化计算,可以取一个传扭销对应部分模型进行分析,最终建立的三维有限元模型如图4所示。实体单元采用Solid 186单元,该单元为高阶3D20节点实体单元,采用二次插值函数,对不规则形状具有良好精度。平面接触和销槽-传扭销接触采用面-面接触单元进行建模,包括接触单元Conta 174和目标单元Targe 170。为了提高计算的收敛性,选用ANSYS提供的指数衰减摩擦模型,取最大静摩擦因数为动摩擦因数的1.25倍,衰减系数为0.6。
图4中前端面施加的压应力用以模拟拉杆预紧力的作用。在工程上,不同截面尺寸的连接轴段预紧力相差很大,而相应的预应力变化范围却很小,因此采用压应力作为研究变量,研究结果更具适用性[13]。前端面外圆弧线上节点施加切向力,用以模拟施加在轴段的扭矩T,后端面采用固定约束。经试算,接触单元的刚度系数K=1时,位移精确度可以满足要求,同时收敛速度也比较适中。表1为带传扭销环形平面接触轴段的相关参数。

图4 带传扭销的环形平面接轴段循环对称有限元模型

参数量值参数量值Ro391.0 mmRi361.0 mmnp12Dp20.0 mmLc30.0 mmPcp80.0 MPaE210.0 MPaν0.3σs302 MPaμs0.25
2.2 传扭特性分析
图5为接触轴段扭转变形随外部扭矩的变化关系。由图5可知,带传扭销的环形平面接触轴段扭转变形表现出明显的双线性特性。FEM分析结果与理论模型计算结果分别用如下的两个线性方程进行拟合
(8)
(9)


图5 带传扭销的环形平面接触轴段扭转变形曲线


表2 双线性扭转刚度和转折点扭矩

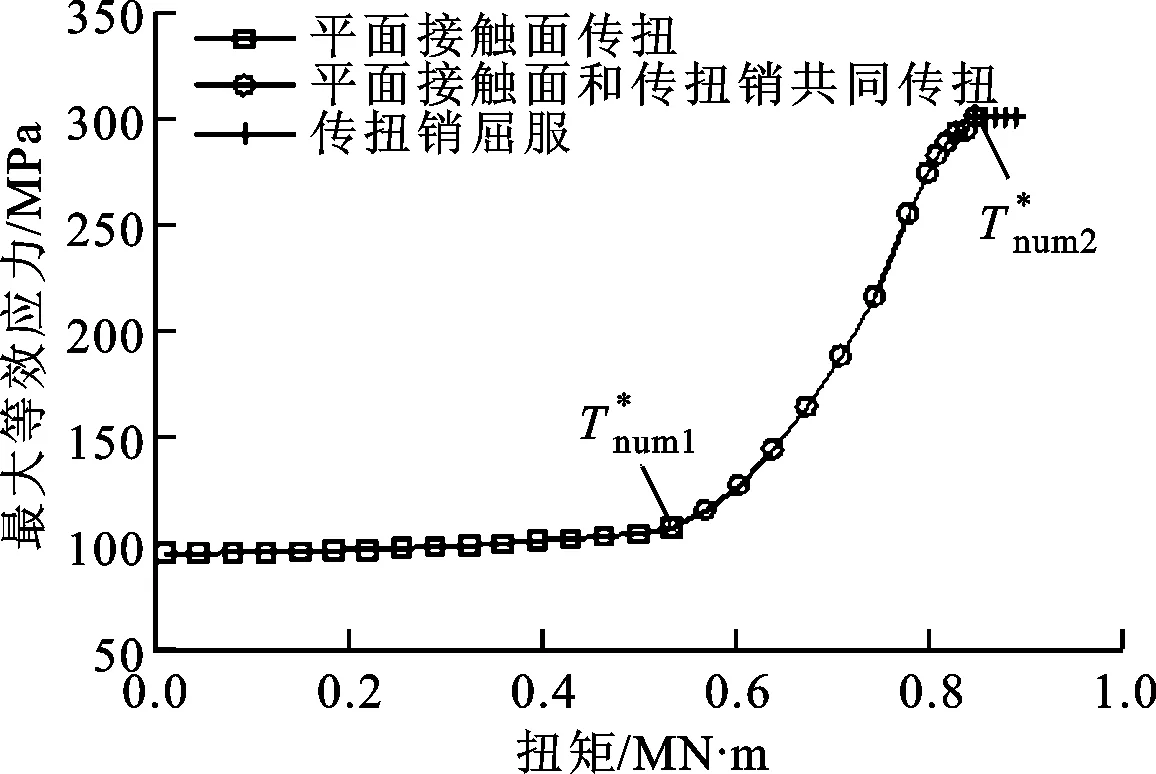
图6 传扭销最大等效应力FEM解
3 参数敏感性分析
3.1 压应力的影响

(a)两个线性段扭转刚度

(b)两个关键点扭矩图7 压应力对接触轴段扭转特性的影响
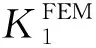
3.2 摩擦因数的影响
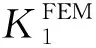

(a)两个线性段扭转刚度

(b)两个关键点扭矩图8 摩擦因数对接触轴段扭转特性的影响
3.3 传扭销数的影响
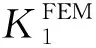

(a)两个线性段扭转刚度

(b)两个关键点扭矩图9 传扭销数对接触轴段扭转特性的影响
3.4 传扭销直径的影响
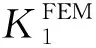

(a)两个线性段扭转刚度

(b)两个关键点扭矩图10 传扭销直径对接触轴段扭转特性的影响
4 结 论
本文针对某重型燃气轮机透平转子压气机盘间带传扭销的环形平面接触轴段的结构特点,提出了其扭转特性的理论分析模型,并通过三维有限元数值计算进行了验证,获得如下结论。
(1)带传扭销的环形平面接触轴段的扭转变形可以用软弹簧特性的双线性模型近似,双线性转折点扭矩大小可通过平面接触面静摩擦力最大传递扭矩近似估计,而整个接触界面的传扭能力可以近似为平面接触面滑动摩擦力传递扭矩与传扭销发生屈服前传递的最大扭矩之和。
(2)第1线性段扭转刚度随着传扭销直径的增加略有减小,摩擦因数对第1线性段扭转刚度影响很小,而压应力和传扭销个数对第1线性段扭转刚度基本没有影响。第2线性段扭转刚度基本不受压应力、摩擦因数和传扭销直径等参数的影响,但随着传扭销个数的增加近似线性增大。
(3)双线性转折点扭矩与压应力和摩擦因数成正比,而与传扭销的个数和直径无关。
本文提出的模型不仅可为重型燃气轮机盘间带传扭销环形平面接触界面的设计提供依据,而且可进一步用于燃机转子的扭转振动分析。盘间带传扭销的环形平面接触轴段的双线性扭转刚度特性会对转子的扭转振动产生影响,有可能使工作中的转子产生非线性振动现象,有待进一步深入研究。

