改进的Powell医学图像配准算法的应用

邢正伟，李海瑛

昆明市延安医院 设备科，云南 昆明 650051

引言

医学图像配准在医学图像处理领域中是一个重要的分支。尤其是当前，医学成像技术的发展速度非常快，不管是在结构还是功能方面，都为临床诊断提供了大量重要实用的影像数据。在临床医学中，单一模态的图像往往不能提供医生所需的足够信息，通常需要配准并融合多模态图像，帮助医生了解病变组织或器官的情况，为临床诊断和手术治疗提供更全面和更准确的信息[1]。医学图像配准[2-3]就是通过寻求一种空间变换，使得两幅医学图像结构上的对应点达成空间上的一致。在实际的临床应用中，计算效率的高低往往是影响医学图像配准发挥作用的关键因素。

医学图像配准可以简单的分为两类：一类是基于图像特征信息的配准，通过提取图像的点、线、面来求取变换参数，达到配准的目的，该方法比较直接、计算量小、速度快，但是精度和鲁棒性不好；另一类方法是基于图像灰度信息的配准，该方法直接利用图像的灰度进行配准，精度高、鲁棒性强、不需要预处理，但是计算量大，速度慢，容易陷入局部极值。

将信息论的原理和方法应用在基于图像灰度信息的配准是一个新的方向。而且，以互信息为相似性测度的配准已经成为一种主流的方法。医学图像配准的实质是配准函数的优化问题，即寻找互信息达到最大时，相关的几个空间变换参数值，最优化方法在配准过程中具有非常重要的地位；但是配准函数经常不是光滑的，存在许多局部极值，这给求解带来了很大难度，从而对配准结果有较大的影响[4]。目前使用基于互信息的医学图像配准的优化算法[5-8]有Powell算法、粒子群优化算法（Particle Swarm Optimization，PSO）及其改进算法、遗传算法、单纯形法等。其中使用较多的优化算法是Powell算法。Powell算法不需要计算导数，在每一维中使用Brent算法迭代搜索，搜索速度比较快，局部寻优能力极强，在局部搜索中精度要高于其他的优化算法[9]。另外，Powell算法在实现过程中一定程度上需要人工的干预。针对不同规格的医学图像，该算法需要专业人员来设定合理的搜索步长，以便获得较好的配准结果，从而在效率、准确性和稳定性之间获得良好的平衡效果。

本文在基于图像灰度信息的配准问题研究上，开展了两个方面的工作。第一，改进了归一化互信息计算中联合直方图的统计方法，突出了感兴趣区域在配准中的决定作用，使得互信息的大小能更准确的反映配准程度。第二，针对Powell优化算法对初始点过度依赖的问题，设计了一种改进算法来寻找配准的初始点，加快了寻优过程中的收敛速度，同时降低了误配准发生的概率。

1 互信息配准的一般理论和方法

1.1 互信息的基本理论

对于在不同时间和不同条件下获取的两幅图像R(x)和F(x)配准，定义一个相似性测度S，并寻找一个空间变换关系T，使得经过该空间变换后，两幅图像间的相似性测度达到最大，也就是图像R上的每一个点在图像F上都有唯一的点与之相对应，并且这两点对应同一解剖位置。

互信息是信息理论中的一个基本概念，通常用于描述两个系统间的统计相关性，或者是一个系统中所包含的另一个系统中信息的多少，它可以用熵来描述，熵表达的是一个系统的复杂性或者是不确定性[9]。

系统A的熵表示为：

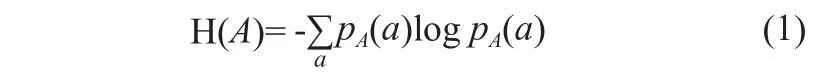
系统B的熵表示为：

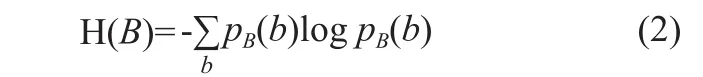
系统A，B的联合熵表示为：

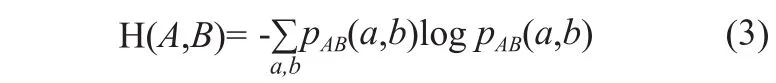
其中a∈A，b∈B。两个系统的互信息可以表示为：

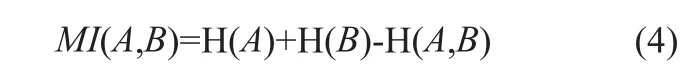
互信息可以作为相似性测度来完成医学图像的配准操作。一般用联合概率分布pAB(a,b)和完全独立时的概率分布p(a)A×pB(b)间的广义距离来估计互信息[10]。

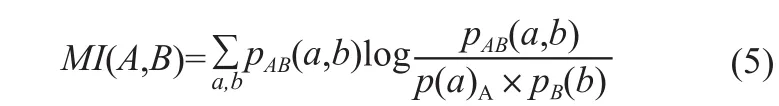
其中联合概率分布pAB(a,b)用两幅图像重叠区域的归一化联合直方图来计算：

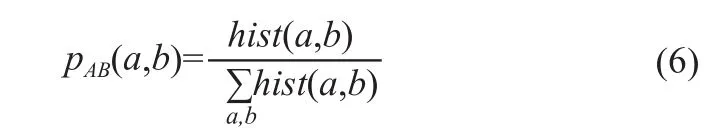
其中边缘概率分布pA(a)、pB(b)的计算方法为：

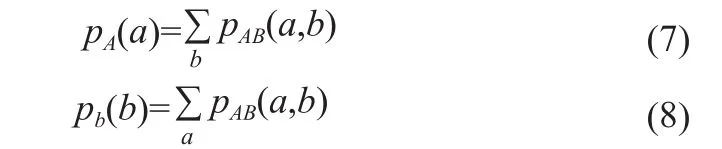
传统互信息对两幅图像重叠程度的变化非常敏感，使得配准过程的互信息变化曲线不光滑，因此本文采用归一化互信息（Normalized Mutual Information，NMI）作为配准的相似性测度，提高配准的稳定性。由式(9)可知，NMI的取值范围是[0, 2]。NMI值的大小反映了配准程度的好坏，当两幅图像完全配准时，NMI达到最大（NMI=2）。NMI(A,B)=[H(A)+H(B)]/H(A,B) (9)

1.2 Powell算法的原理

在医学图像配准领域中最常用的优化算法是Powell算法，该算法是一种局部多参数局部最优化算法，相对于全局优化算法来说有较快的收敛速度，但对于大规格的图像来说，仍有提升的空间；该算法容易受到局部极值的影响陷入误配准，其改进的关键在于初始点的选择。在每一次迭代中，都要从初始点开始进行一维搜索，搜索的方向是Powell算法中的另一个重要参数，用一个多方向集C来表示。当参数的导数不易计算时，应用多方向集算法[11-13]这个概念，就可以把多元函数的求解问题转化为求取一维极值的问题。

Powell算法具体的优化过程分为若干次迭代，每次迭代都由N+1次一维搜索组成，其中N是搜索空间的维度，例如二维图像刚性变换配准的搜索空间维度是3，分别是水平方向、垂直方向和旋转方向。算法每次迭代过程的步骤是，从初始点开始，依次沿方向集的N个方向进行一维搜索，得到一个最佳值及最佳值对应的点。然后沿该点和初始点的连线的方向进行搜索，求得本次迭代的最佳值及最佳值对应的点，然后把连线的方向替换前N个方向中效果不好的方向，形成新的方向集，进行下一次迭代。

具体构造过程如下：① 将方向集ci初始化：ci=e（i=1,2,…,N，e为坐标轴的单位向量）；② 记录初始点位置P0；③ 从Pi出发，依次沿方向集的各个方向寻找该方向归一化互信息的极大值点，记该点为Pi+1，以该点为新的出发点，进行下一次迭代搜索；④ 重复步骤（3），直到新找到的点和前一点之间的距离＜ε(ε为设定精度值)，则跳出循环，把该点作为算法的解。

2 算法的改进

2.1 归一化互信息的改进

使用改进算法进行初始点寻优的时候，对于大规格的图像会存在精度不准确的情况，因为图像的背景区域太大，而有效信息区域在整幅图像中的比例过小。针对这种情况需要对联合直方图的计算方法进行改进，以提高改进算法的稳定性。

在计算联合直方图的时候需要用到插值算法（图1），因为当浮动图像经过变换到参考图像的坐标网格中时，像素点所在的位置不一定是和参考图像的像素点重合的。这就需要我们使用插值算法来计算变换后点的像素值。现代配准算法一般采用的是部分体积插值算法（Partial Volume Interpolation，PV），我们也采用PV算法来计算像素值。

如图1所示，在每一次计算互信息值大小的时候，根据变换参数，变换T都会把浮动图像F上的点Pf（i,j）变换到参考图像R上的点Pr，坐标为（x+Δx,y+Δy）。如果要用一般的PV算法来计算点Pr的灰度值，引进了图像原本不存在的灰度值，计算量太过庞大，在实际的编程中，联合直方图采用如下公式的计算方法。

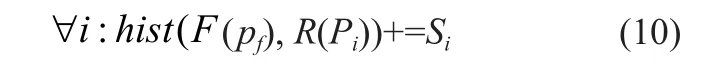
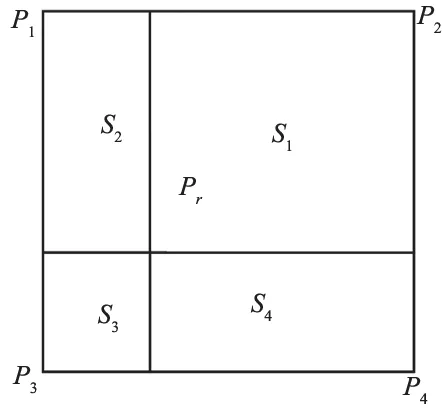
图1 PV插值算法示意图

如果要放大感兴趣部分在整幅图像中的权重，则需要把hist中背景部分的计算量缩小，具体的计算公式如下：

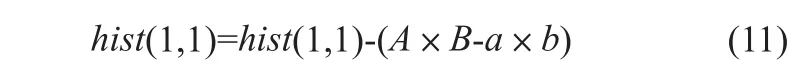
其中A，B分别是参考图像的长和宽，a，b分别是剔除背景后的图像在图像坐标系中水平方向和垂直方向的最大和最小坐标。这样就降低了背景区域在联合直方图中的作用，避免了因为背景重合的局部极值造成的误配准，也增加了寻找初始点算法的精确度和稳定性。

归一化互信息的各部分分量在配准过程中的变化曲线，见图2。

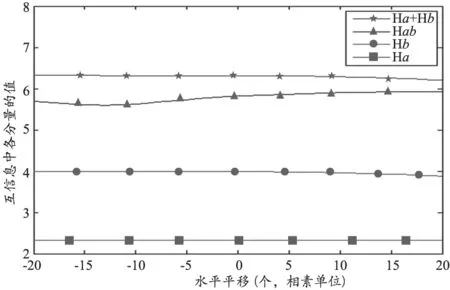
图2 互信息中各分量的变换曲线

如图2所示，在计算联合直方图的时候，a代表参考图像，b代表浮动图像。浮动图像b中的每个像素点都被计算在内，对直方图的贡献权值为1，故图像b的信息熵Hb是一常量，其变化曲线是水平的。而参考图像a的部分像素点没有被计入联合直方图的计算，其信息熵Ha为一变量。因此在计算归一化互信息的时候可以保留参考图像的信息熵，舍弃浮动图像的信息熵，来简化归一化互信息的计算，同时保留与原来相似性测度相同的收敛特性。改进的归一化互信息计算公式如下所示：

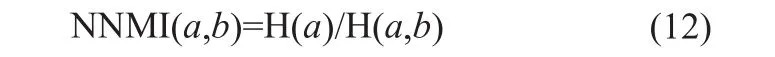
2.2 寻优算法的改进

要想节省优化过程的时间，根本在于减小迭代的次数。以下以二维图像刚性变换配准为例，分别对3个搜索方向的互信息变换曲线进行研究。

选取一幅图像作为参考图像，以参考图像水平方向向左平移5个像素，垂直方向向上平移13个像素，顺时针旋转10°得到的图像为浮动图像，以参考图像和浮动图像对齐时默认位置为初始点。把浮动图像以图像中心为原点，向左平移20个像素至向右平移20个像素，求取平移后图像与原参考图像的互信息，得到在该方向上的互信息测度变化曲线，见图3a。在垂直方向上下移动20个像素和旋转方向逆时针至顺时针旋转10°得到的互信息测度变换曲线，见图3b和图3c。

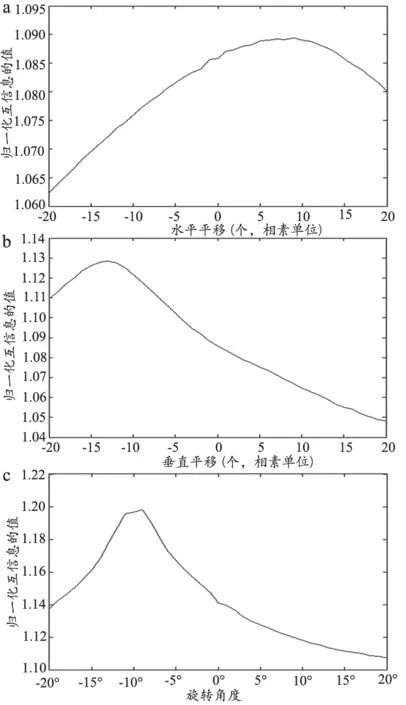
图3 待配准的两幅图像相对移动得到的归一化互信息曲线

由图3可见该曲线在预设的参数值附近达到最大值，说明完全可以设计一种简单的算法来求取该值的大小作为Powell算法的初始点，避免Powell算法前期漫长的寻优过程和大量的计算，加快算法的收敛速度，提高图像配准的速度。

平移变换初始点的计算方法如下：先计算参与配准的两幅图像在初始位置V0（0,0,0）的互信息值F0。因为平移变化较旋转变化的互信息曲线更加光滑，故先从水平方向进行计算。计算初始位置向左和向右平移一个像素单位的互信息值，选取互信息值增加的一侧为寻优方向，不断搜索，直到互信息值开始减小。如果前进一个像素单位互信息值增加，则继续搜索，如果互信息值继续减小，则跳出循环，返回前一个点对应的坐标x0作为新的初始点V0（x0,0,0）。从新的初始点V0（x0,0,0）开始，在垂直方向按照同样的方法寻找极值点y0。由于在旋转方向互信息曲线的局部极值较多，故使用上面的方法来求取极值点容易陷入局部极值。旋转角度都有一定的限度，故对于旋转方向的极值点求取要采取新的方法。计算[-180, 180]范围内每个整数单位处的互信息值，求其中的最大值，作为旋转方向的极值点θ0。最终得到点V0（x0,y0,z0）作为下一步Powell算法的初始点。

具体的实现步骤如下：

（1）默认参与配准的两幅图像初始位置的点V0（0,0,0）为初始点，令x0=0，y0=0，z0=0，计算该点的互信息值F(0,0,0)。

（2）计算浮动图像在水平方向平移+1，-1个像素的互信 息 值 F(+1,0,0)和 F(-1,0,0)。 如 果 F(+1,0,0)-F(0,0,0)＞0，则令e=1，否则，令e=-1，此时x0=e。

（3）若 F(x0+e,0,0)-F(x0,0,0)＞0，则 x0=x0+e，重复步骤（3）。

（4） 当 F(x0+e,0,0)-F(x0,0,0)＜0时， 如 果 F(x0+2e,0,0)-F(x0,0,0)＞0，则x0=x0+e，重复步骤（3）；如果F(x0+2e,0,0)-F(x0,0,0)＜0，则跳出循环，返回水平方向的初始值x0。

（5）以点V0（x0,0,0）为初始点，计算该点的互信息值F(x0,0,0)。计算浮动图像在垂直方向平移+1，-1个单位后的互信息值F(x0,+1,0)和F(x0,-1,0)。如果F(x0,+1,0)-F(x0,0,0)＞0，则令e=1，否则，令e=-1，此时y0=e。

（6）若 F(x0,y0+e,0)-F(x0,y0,0)＞0，则 y0=y0+e，重复步骤（6）。

（7）当F(x0,y0+e,0)-F(x0,y0,0)＜0时，如果F(x0,y0+2e,0)-F(x0,y0,0)＞0，则 y0=y0+e，重复步骤（6）；如果 F(x0,y0+2e,0)-F(x0,y0,0)＜0，则跳出循环，返回垂直方向的初始值y0。

（8）以点 V0（x0,y0,0）为初始点，计算 z0在 [-180，180]范围内每个整数点处的互信息值Fi，求得其中的最大值Fmax以及最大值对应的点θ0。

（9）以点 V0（x0,y0,θ0）作为Powell算法的初始点。

该算法不仅能减少优化算法的迭代时间，而且对于角度旋转方向来说，可以越过大部分的局部极值，见图4，可以看出互信息曲线在角度不断变化的情况下有许多个局部极值，而本算法在全局范围内的搜索，跳出了这些局部极值的干扰，能有效的计算出最大值在10°左右。

3 实验数据及结果

为验证算法的有效性和稳定性，本文采用了不同的医学图像进行验证。

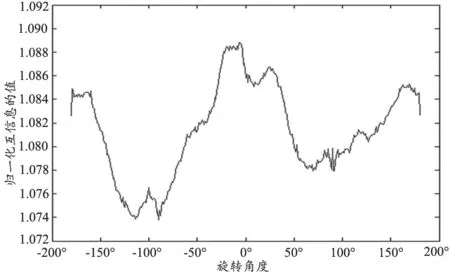
图4 旋转一周的互信息曲线

实验一采用了Brain Web的脑部磁共振T1加权图像[14-15]，图像大小为181×217×181。任意选取其中的一帧作为参考图像，见图5a。参考图像在水平方向、垂直方向和旋转方向做不同的参数变化，得到的图像作为浮动图像，见图5b。图5b是图5a向右平移10个像素，向下平移12个像素，逆时针旋转10°得到的。

图5 实验一所用图像

制作了5组浮动图像，每组浮动图像都是参考图像在水平、垂直方向平移一定的距离，并旋转一定的角度形成的。实验分别采用经典Powell算法，PSO算法（以传统归一化互信息为相似性测度）和本文的改进算法3种算法对实验图像进行配准操作，每次配准分别独立运行10次取平均值。

具体的配准结果，见表1。其中x、y、ang分别是图像在水平，垂直和旋转方向的变换参数，x、y的单位是像素，ang的单位是度（°）。变换参数是（20,20,1）时，经典Powell算法出现了配准失败的情况，而改进算法得到的变换参数和预设参数的误差在亚像素的精度范围内，并未出现配准失败的情况，比经典Powell算法更稳定。在速度方面，改进的算法也比传统的算法快很多。

实验二采用的图像是Vanderbilt大学提供的病人的CT图像，图像大小为512×512×29[15]。任意选取其中的一帧作为参考图像[16]，见图6a。参考图像在水平方向，垂直方向和旋转方向做不同的参数变化，得到的图像作为浮动图像，见图6b。图6b是图6a向右平移10个像素，向下平移12个像素，顺时针旋转10°得到的。

制作了5组浮动图像，每组浮动图像都是参考图像在水平、垂直方向平移一定的距离，并旋转一定的角度形成的。实验分别采用经典Powell算法、PSO算法（以传统归一化互信息为相似性测度）和本文的改进算法3种算法对实验图像进行配准操作，每次配准分别独立运行10次取平均值。具体的配准结果，见表2。

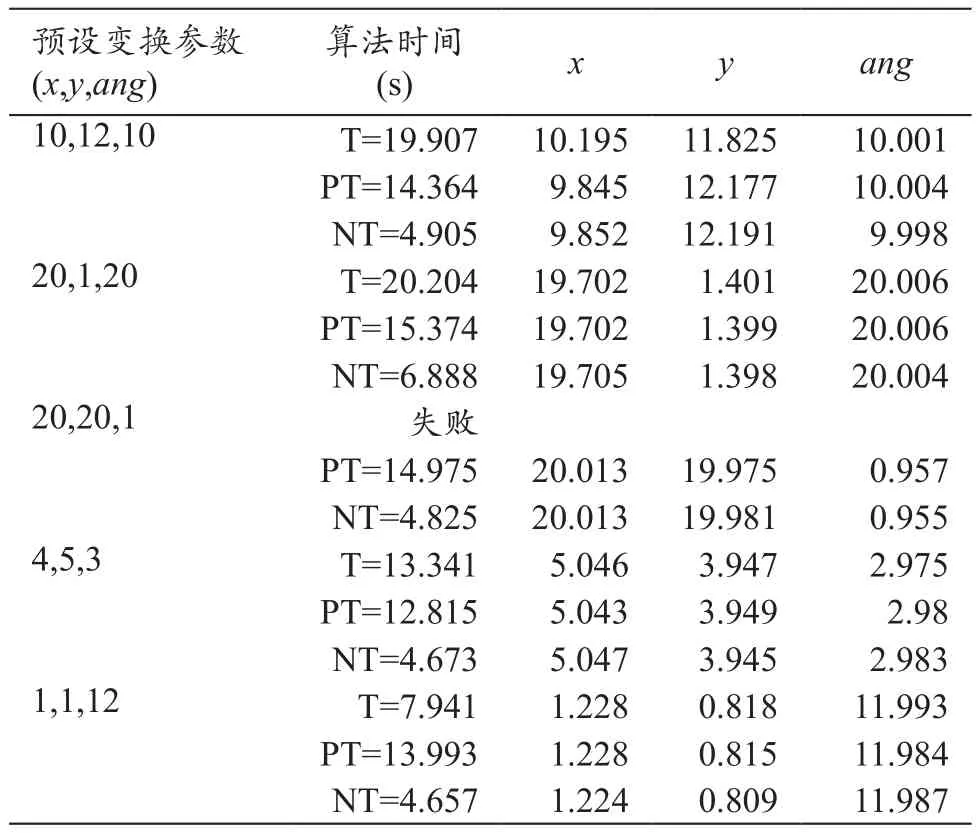
表1 实验一的配准结果

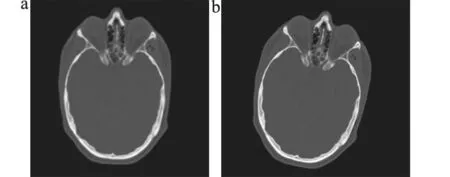
图6 实验二所用图像

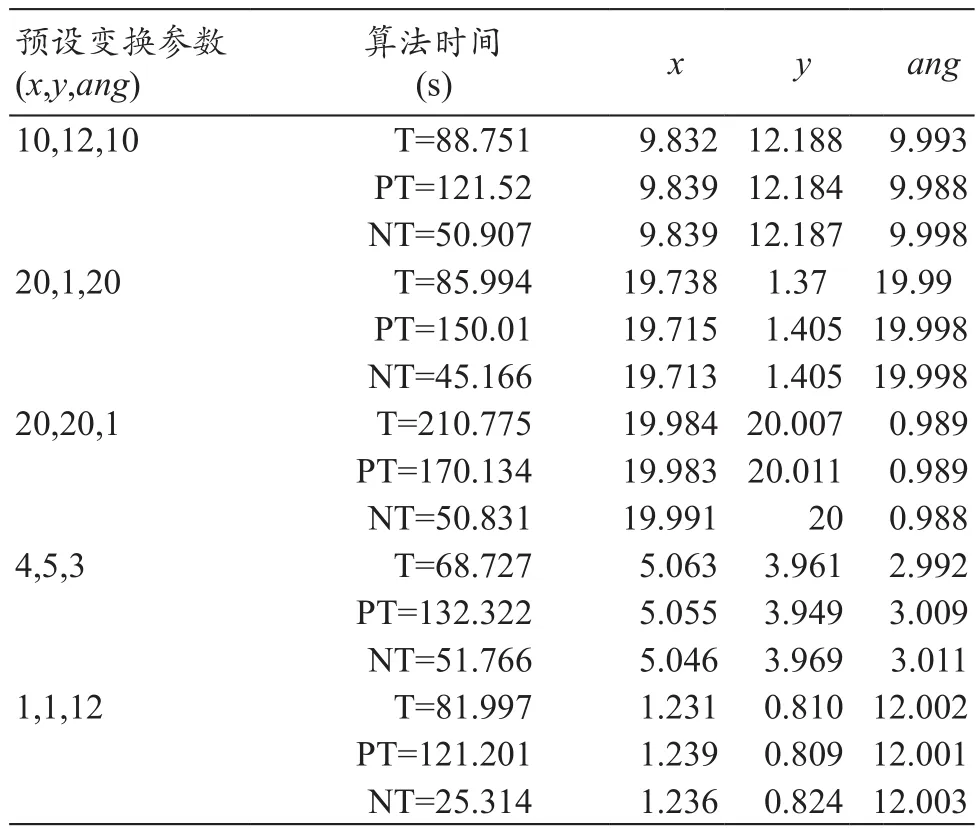
表2 实验二的配准结果

由表2可以看出，本文的改进算法在精度方面，得到的变换参数和预设参数的误差在亚像素的精度范围内，满足配准的理论要求和临床需要；在速度方面，改进的算法比PSO算法至少快一倍以上，比传统的Powell算法也要快的多。

4 结论

本文针对传统互信息图像配准中Powell算法的自动化程度不高、配准时间长和易受局部极值影响而出现误配准的问题从两个方面进行了改进。一是改进了Powell算法中初始点的寻找方式，节省了优化初期过多的迭代量，减少了配准所需要的时间，同时提高了配准的自动化程度。二是改进了归一化互信息的计算公式及其联合直方图的计算方法，突出了感兴趣区域在相似性测度中的作用，使得互信息能更准确的反应配准的程度，减小误配准的几率。实验证明了本方法的有效性。

[参考文献]

[1] 郑莹,李光耀.区域和局部信息结合的双向医学图像配准[J].中国图象图形学报,2011,16(1):90-96.

[2] 张汗灵,杨帆.基于互信息和混合优化算法的多模医学图像配准[J].湖南大学学报:自然科学版,2006,33(1):117-120.

[3] 杨日容.基于遗传算法及最大互信息的医学图像配准研究[D].昆明:昆明理工大学,2005.

[4] 方伟,孙俊,丁彦蕊,等.医学图像配准的混合量子粒子群优化算法研究[J].计算机工程与应用,2011,47(3):166-169.

[5] 刘斌,彭嘉雄.图像配准的小波分解方法[J].计算机辅助设计与图形学学报,2003,15(9):1070-1073.

[6] Pardalos PM,Shalloway D,Xue G.Optimization methods for computing global minima of nonconvex potential energy functions[J].J Global Optim,1994,4(2):117-133.

[7] Nelder JA,Mead R.A simplex method for function minimization[J].Comput J,1965,7(4):308-313.

[8] Wilkinson B,Allen M.Parallel Programming: Techniques and Applications Using Networked Workstations and Parallel Computers[M].北京:高等教育出版社,2002.

[9] 方伟,孙俊,丁彦蕊,等.医学图像配准的混合量子粒子群优化算法研究[J].计算机工程与应用,2011,47(3):166-169.

[10] Pluim JPW,Maintz JBA,Viergever MA.Mutual-informationbased registration of medical images: a survey[J].IEEE T Med Imaging,2003,22(8):986-1004.

[11] 袁伟,时公涛,蒋咏梅.一种基于ROEWA算子和GA-Powell算法的SAR图像配准方法[A].第十四届全国信号处理学术年会(CCSP-2009)论文集[C].2009.

[12] Ding H,Bian ZH.A sub-pixel registration approach based on powell algorithm[J].Acta Photonica Sinica,2009,38(12):46-49.

[13] 刘叶青,刘三阳,谷明涛.Powell算法在线性支持向量机中的应用[J].计算机工程,2011,37(12):161-163.

[14] 冯林,管慧娟,滕弘飞.基于互信息的医学图像配准技术研究进展[J].生物医学工程学杂志,2005,22(5):1078-1081.

[15] 彭景林,章兢,李树涛.基于改进PV插值和混合优化算法的医学图像配准[J].电子学报,2006,34(5):962-965.

[16] 冯林,严亮,黄德根,等.PSO和Powell混合算法在医学图像配准中的应用研究[J].北京生物医学工程,2005,24(1):8-12.