基于混合储能和能量捕获的多接入信道容量建模与分析

姚信威，章梦娜，王超超，王万良



基于混合储能和能量捕获的多接入信道容量建模与分析

姚信威，章梦娜，王超超，王万良

（浙江工业大学计算机科学与技术学院，浙江 杭州 310023）

能量捕获具有部署灵活和可持续供能的优点，已成为解决物联网中设备能量受限的有效途径之一。针对基于能量捕获的多接入信道，能量捕获技术存在能量来源不稳定、存储设备容量有限等因素，因此采用基于超级电容和电池的混合储能结构。根据其信道的特点和能量捕获的随机特性，引入节点能量约束关系，提出了一种呈指数型下降（ETD）的近似最优能量分配策略对平均吞吐量进行分析，推导其上下界及其常数差值。最后利用平均吞吐量和信道容量的关系求得近似信道容量。实验分析了捕获能量、储能容量以及节点数目对多接入信道容量的影响，同时实验结果表明，相比传统节点采用电池作为单一储能单元，采用混合储能结构可以有效地提高节点的捕获能量数值，使其在信号的发送上采用多进制的传输方式，进而增大多接入信道的容量。

物联网；能量捕获；混合储能；信道容量；能量分配

1 引言

随着物联网技术和无线通信技术的发展，节点的供能问题已经成为制约其广泛应用的主要因素。而能量捕获（EH, energy harvesting）技术的兴起，使具备能量捕获能力的设备相较于传统的有线电或电池供电的设备具有明显的优势，节点通过能量捕获模块可以从周围环境中收集多种类型的能量，例如机械能、热能和电磁辐射等[1-2]，并将其转换为电能，从而达到设备可持续利用的目的。因此，将能量捕获技术作为解决无线网络节点供能问题的一种可行方案，吸引了学术界与产业界的广泛关注，同时也取得了显著的进展。

在物联网场景中，环境的能量源具有间歇性、随机性等特点，从而使捕获能量到达的时间以及量值较难预测[3]。因此，传统的物联网中节点由电网或电池供能，节点电池能量能够保证稳定的数据传输；而基于能量捕获的物联网中，捕获能量的动态变化特性使节点中可用于数据传输的能量是间断、不连续的，在某个时刻节点可能因为捕获能量的不足而发生数据传输中断[4]。

近年来，为了从理论层面系统地了解基于能量捕获的网络数据传输速率受限问题，一些学者开始针对无线传感器网络中基于能量捕获的通信信道容量问题展开研究[5-15]。针对单一电池储能结构的点对点信道容量的研究已有许多的研究成果[5-12]，研究表明，基于能量捕获的通信信道容量主要由节点电池储能容量和捕获能量值2个参数决定。当节点电池储能容量无限大时，研究成果证明，基于能量捕获的通信信道容量与平均能量捕获速率的约束关系和基于传统加性高斯白噪声的通信信道容量与平均发送速率的约束关系等价[5-6]。当节点电池储能容量有限时，基于能量捕获的通信信道容量求解仍然是个开放性的难题。文献[7]分析基于能量捕获的二元信道的信道容量问题。文献[8]在Verdu-Han通用结构的基础上，提出了一种信道容量的计算方法，并进一步采用最优能量管理策略推导信道容量的下界。当节点电池储能容量有限并且捕获能量为定值时，利用文献[9]求解基于能量捕获的信道容量的边界。文献[10]分析基于能量捕获的瑞利衰减信道的近似信道容量。文献[11]通过设计编码策略，将功率控制问题与信道容量求解问题相结合，通过计算得出信道容量的近似值。文献[12]基于节点电池容量有限的情形给出基于能量捕获的信道容量的表达式，并推导信道容量的上下界限。相比于针对点对点信道容量的研究，国内外针对多节点网络信道模型的信道容量的研究较少[13-15]。其中，文献[13]针对节点电池容量无限的多接入信道进行了分析，文献[14-15]针对节点电池容量有限的多接入信道进行了分析。

目前，现有的物联网节点或设备普遍采用电池作为单一的能量存储单元，因此，基于能量捕获的通信信道容量的研究都是以此为基础的。然而，针对在实际应用环境中存在捕获能量动态变化和电池存储效率低的特性，本文采用混合能量存储结构（由电池和超级电容组成）作为物联网的储能单元。在文献[16-17]中已证明，相比于采用单一电池储能结构，采用电池和超级电容的混合储能结构可以提高整个网络的性能。考虑实际物联网中多个传感区域的传感器节点同时向汇聚节点发送数据的场景，如图1所示。因此，本文针对该场景下的多接入信道，分析基于能量捕获的多接入信道容量，首先建立基于混合储能和能量捕获的多接入信道模型，在全面分析信道模型特点的基础上，综合考虑捕获能量的动态随机特性，采用一种近似最优能量分配策略（ETD）求解基于混合储能和能量捕获的多接入信道平均吞吐量的上下界，并进一步求得信道容量。

图1 物联网中感知网络场景

2 系统模型

图2 基于混合储能的能量捕获多址接入通信信道模型

3 能量分配策略

3.1 近似最优能量分配策略

图3 节点能量捕获模型

图4 ETD策略下的能量变化关系

3.2 平均吞吐量上下界

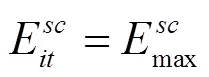
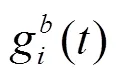
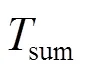
代入式(4)和式(5)，并由式(8)和式(9)可得

将式(17)等式右边分成2个部分分别进行计算，对第一部分进行变换，为

对式(17)等式右边的第二部分进行如式(19)所示的变换。

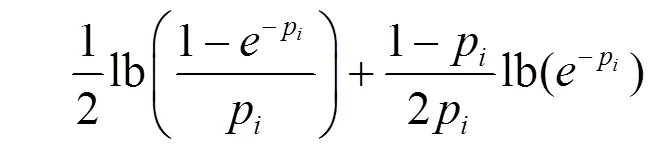
因此，式(16)最终可以推导为

即有

对式(21)进行推导，可以得到

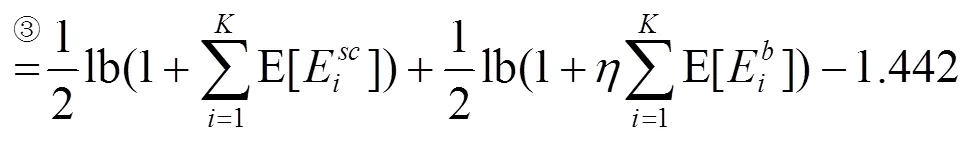
假设发射节点在第一次捕获能量到达之前初始能量为0，根据消耗能量不大于总的可用能量，有如下能量受限关系，为

对式(30)进行变形为

式(32)中推导过程①是由对数函数的凹凸性质得到，推导过程②由式(31)得到，推导过程③是由于节点捕获能量小于超级电容，则节点消耗超级电容中的总能量不大于节点总的捕获能量，进而得到最终结果。至此，求得了系统平均吞吐量的一个上界，下面将采用3.1节给出的ETD策略对系统平均吞吐量的下界进行分析。

对式(33)进行与式(18)类似的变换，可以得到

根据对式(34)的求解，可以得到

综上，结合式(32)和式(37)可得系统的平均吞吐量的上下界为

4 系统的信道容量

在第3节里已经分别求得了捕获能量小于节点总储能容量同时大于超级电容容量、捕获能量小于超级电容容量、捕获能量大于总储能容量3种情形下的系统平均吞吐量的上下界，本节将依据文献[15]中得出的系统信道容量与系统平均吞吐量的关系，进一步求得系统的近似信道容量。

文献[15]针对节点采用电池作为单一储能结构，基于能量捕获的多接入信道容量进行了分析，根据文献[15]中的定理2和定理3可以得到，当发射节点和接收节点已知能量到达的因果关系的情形时，信道容量与平均吞吐量为

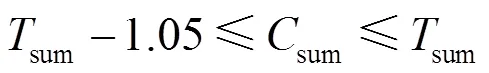
综合第3节中针对不同情况下求得的系统平均吞吐量的上下界和式(42)，可以得到信道容量如下所示。

5 仿真实验和分析

1) 信道容量与捕获能量的关系

图5 2种储能模型在情形下的结果比较

图6 2种储能模型在情形下的结果比较

2) 信道容量与储能容量的关系

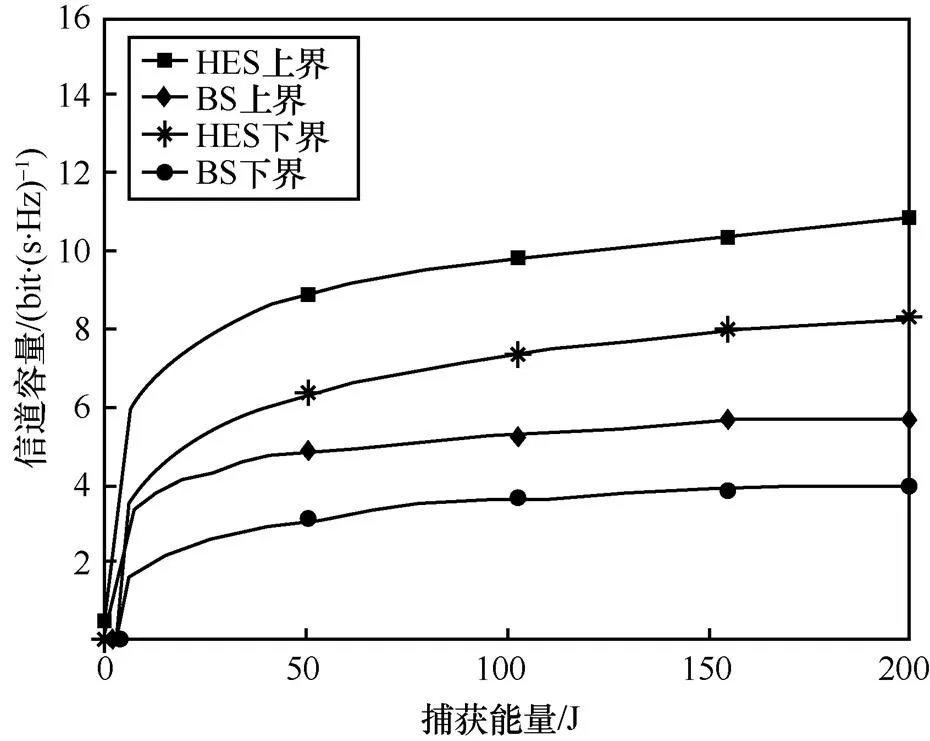
图7 2种储能模型在不同储能容量下的结果对比

3) 信道容量与节点数目的关系

为了分析节点数目对系统信道容量的影响，进行2组实验，分别取和，并且在基于捕获能量充足的情形下进行实验，仿真实验如图8所示。由图8可知，信道容量随着节点数目的增加而增大，而系统信道容量上下界之间的差值保持恒定不变，为2.49 bit∙(s∙Hz)−1。因此，当节点数目趋于无穷大时，随着信道容量的不断增大，其上下界的恒定差值可以忽略不计。

图8 2种储能模型在不同节点数目情形下的结果对比

6 结束语

本文对多接入能量捕获通信信道容量进行了分析，每个发射节点采用电池和超级电容的结构，且每个节点捕获能量平均值相等。根据能量到达的随机特性，假设能量到达服从独立同分布的伯努利随机分布，且每个节点捕获能量的平均值相等。通过对每个节点采用ETD策略推导出了系统平均吞吐量的上下界，并进一步求得系统的近似信道容量。单位时间内，当捕获能量小于超级电容存储容量时，系统信道容量上下界之间的常数差值为1.77 bit∙(s∙Hz)−1；当捕获能量大于超级电容存储容量情形时，系统信道容量上下界之间的常数差值为2.49 bit∙(s∙Hz)−1。仿真实验分析了系统信道容量与捕获能量、储能容量以及节点数目的关系，实验表明，相比节点采用单一电池储能，采用混合储能结构可以有效地提高节点的捕获能量数值，使其在信号的发送上采用多进制的传输方式，进而增大系统的信道容量。

[1] 韩江洪, 丁煦, 石雷, 等. 无线传感器网络时变充电和动态数据路由算法研究[J]. 通信学报, 2012, 33(12):1-10.

HAN J H, DING X, SHI L, et al. Research on the time-varying charging and dynamic data routing strategy for rechargeable wireless sensor networks[J]. Journal on Communications, 2012, 33(12): 1-10.

[2] PARADISO J A, STARNER T. Energy scavenging for mobile and wireless electronics[J]. IEEE Pervasive Computing, 2005, 4(1):18-27.

[3] OZEL O, TUTUNCUOGLU K, ULUKUS S, et al. Fundamental limits of energy harvesting communications[J]. IEEE Communications Magazine, 2015, 53(4):126-132.

[4] YAO X W, WANG C C, WANG W L, et al. On the achievable throughput of energy-harvesting nanonetworks in the terahertz band[J]. IEEE Sensors Journal, 2018, 18(2): 902-912.

[5] OZEL O, ULUKUS S. Achieving AWGN capacity under stochastic energy harvesting[J]. IEEE Transactions on Information Theory, 2012, 58(10):6471-6483.

[6] RAJESH R, SHARMA V, VISWANATH P. Capacity of Gaussian channels with energy harvesting and processing cost[J]. IEEE Transactions on Information Theory, 2014, 60(5):2563 - 2575.

[7] TUTUNCUOGLU K, OZEL O, YENER A, et al. Binary energy harvesting channel with finite energy storage[C]//IEEE International Symposium on Information Theory. 2013: 1591-1595.

[8] MAO W, HASSIBI B. On the capacity of a communication system with energy harvesting and a limited battery[C]//IEEE International Symposium on Information Theory. 2013: 1789-1793.

[9] JOG V, ANANTHARAM V. An energy harvesting AWGN channel with a finite battery[C]//IEEE International Symposium on Information Theory. 2014: 806-810.

[10] DOSHI J, VAZE R. Long term throughput and approximate capacity of transmitter-receiver energy harvesting channel with fading[C]//IEEE International Conference on Communication Systems. 2015: 46-50.

[11] DONG Y, FARMIA F, OZGUR A. Near optimal energy control and approximate capacity of energy harvesting communication[J]. IEEE Journal on Selected Areas in Communications, 2014, 33(3):540-557.

[12] SHAVIV D, NGUYEN P M, OZGUR A. Capacity of the energy harvesting channel with a finite battery[C]//IEEE International Symposium on Information Theory. 2015:131-135.

[13] RAJESH R, DEEKSHITH P K, SHARMA V. Capacity of a Gaussian MAC with energy harvesting transmit nodes[C]// Information Theory and Applications Workshop. 2012:338-343.

[14] INAN H A, OZGUR A. Online power control for the energy harvesting multiple access channel[C]// International Symposium on Modeling and Optimization in Mobile, Ad-Hoc and Wireless Networks. 2016:1-6.

[15] INAN H A, SHAVIV D, OZGUR A. Capacity of the energy harvesting Gaussian MAC[C]//IEEE International Symposium on Information Theory. 2016: 2744-2748.

[16] CAO J, EMADI A. A new battery/ultracapacitor hybrid energy storage system for electric, hybrid, and plug-in hybrid electric vehicles[J]. IEEE Transactions on Power Electronics, 2011, 27(1):122-132.

[17] SAGGINI S, ONGARO F, GALPERTI C, et al. Supercapacitor-based hybrid storage systems for energy harvesting in wireless sensor networks[C]// Applied Power Electronics Conference and Exposition. 2010: 2281-2287.

[18] JING Y, ULUKUS S. Optimal packet scheduling in an energy harvesting communication system[J]. IEEE Transactions on Communications, 2010, 60(1):220-230.

[19] OZEL O, TUTUNCUOGLU K, YANG J, et al. Transmission with energy harvesting nodes in fading wireless channels: optimal policies[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(8):1732-1743.

[20] 姚信威, 郑星航, 王万良, 等. 吞吐量最大化的二维无线能量传输算法[J]. 计算机科学, 2015, 42(11): 164-169.

YAO X W, ZHENG X H, WANG W L, et al. A bidimensional wireless energy transfer algorithm for maximum network throughput[J]. Computer Science, 2015, 42(11): 164-169.

Modeling and analysis of multiple access channel capacity based on hybrid energy storage and energy harvesting

YAO Xinwei, ZHANG Mengna, WANG Chaochao, WANG Wanliang

College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China

Energy harvesting (EH) has been considered as a promising technology to solve the constrained energy problem in the devices of IoT with its advantages of flexible deployment and sustainable energy supply. For multiple access channel with energy harvesting, a hybrid energy storage structure model composed by super capacitor and battery was proposed for the devices of IoT. According to the peculiarities of medium access channel and energy harvesting system, an optimized energy allocation strategy with exponential-type decline (ETD) was presented, the upper and lower bounds of the average throughput were deduced, in particular, the gap of two bounds was derived to be a constant. The channel capacity was further obtained by utilizing the relationship between the average throughput and the channel capacity. In the simulations, the effect of harvested energy, storage capacity and the number of nodes on the channel capacity were analyzed respectively. Experiment results show that compared with the conventional wireless node with single battery storage, the proposed hybrid energy storage structure can improve the harvested energy value and increase the multiple access channel capacity by using adaptive modulation scheme when transmitting the signals.

IoT, energy harvesting, hybrid energy storage, channel capacity, energy allocation

TN925

A

10.11959/j.issn.1000−436x.2018139

姚信威（1986−），男，浙江诸暨人，博士，浙江工业大学副教授、博士生导师，主要研究方向为多尺度智能感知与通信/无线能量传输、物联网、智能大数据等。

章梦娜（1993−），女，浙江绍兴人，浙江工业大学硕士生，主要研究方向为无线能量传输、移动机器人技术等。

王超超（1992−），男，浙江嘉兴人，浙江工业大学博士生，主要研究方向为微观尺度智能感知与通信、物联网和移动机器人技术等。

王万良（1957−），男，江苏高邮人，博士，浙江工业大学教授、博士生导师，主要研究方向为人工智能、物联网、大数据、网络控制等。

2017−10−03；

2018−07−23

姚信威，xwyao@zjut.edu.cn

国家自然科学基金资助项目（No.61772471, No.61771430）

The National Natural Science Foundation of China (No.61772471, No.61771430)