在建构数学问题情境中培育学生数学核心素养

江苏省宜兴市官林实验小学教育集团 郭剑峰

一、要善于紧抓学生的心理需求

著名特级教师于漪曾说过：“课的第一锤要敲在学生的心灵上，激发起他们思维的火花，或像磁石一样把学生牢牢地吸引住。”一节课的开始是否能很快抓住学生的心，对一节课的成败非常关键。一上课，学生其实在生理和心理上都没有做好学习的准备，甚至还停留在课间的十分钟，这时更需要教师精心设计问题情境，让学生不经意间掉进教师设置的“陷阱”，从而激发他们的学习兴趣、唤醒思维，达到最佳学习状态。

如在学习复式统计表前，做个抢答游戏：

观察四张单式统计表抢答：

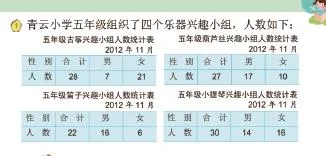
1.五年级葫芦丝兴趣小组有几名男生？2.五年级笛子兴趣小组男生多还是女生多？3.五年级哪个小组人数最多？4.五年级四个兴趣小组一共有多少人？

抢答过程中学生发现，1、2两题回答很快；3、4两题回答速度明显慢了很多，因为1、2两题的答案在同一张统计表中，3、4两题要整合四张表的信息，信息分散，不易迅速作答，所以学生在心理上就有把四张表的信息整合在一张表上的需求，也就有了学习复式统计表的需求。笔者用抢答游戏的方式，结合学生实际情况，创设问题情境，唤起学生的注意力，激发学生的学习需求，使学生主动、积极地投入到学习过程中。

二、要直击学生的兴趣爱好

托尔斯泰说过：“成功的教学所需要的不是强制，而是激发学生的兴趣。”可见兴趣对数学教学的成功起着定向作用，数学教学上的成就很大程度取决于学生对数学课的兴趣是否保持和发展。只有当学生对问题有了强烈的兴趣，才可能对问题大胆地去探究。学生能否大胆思考，善于思考，决定着学生对知识的牢固掌握和灵活运用程度。从学生兴趣出发，创设问题情境，能促使学生掌握和运用知识，促进创新思维能力的形成和发展，从而为学习更高层次的知识奠定坚实的基础。

例如在小数加、减法综合练习时出示：3.86+2.75+（ ）。

师：看着题，教师觉得计算很有难度，你能在括号里填写一个小数，使计算简单些吗？

求变、求简正是学生的兴趣所在，一下子思维活跃起来：“0.14、0.25”“1.14、2.14、3.14……”“1.25、2.25……”“凑成整数就行了。”学生在教师创设的情境引领下，体验了根据数的特点合理简便的过程，训练了学生发散、有序、创新的思维，让不同层次的学生实现了思维的拔节生长，发展了学生的数学素养。

三、要紧抓学生的最近发展区

维果斯基的“最近发展区理论”认为学生的发展有两种水平：一种是学生的现有水平，指独立活动时所能达到的解决问题的水平；另一种是学生可能的发展水平，也就是通过教学所获得的潜力。两者之间的差异就是最近发展区。教学应着眼于学生的最近发展区，为学生提供带有难度的内容，调动学生的积极性，发挥其潜能，超越其最近发展区而达到下一发展阶段的水平，然后在此基础上进行下一个发展区的发展。

出示纸条2：

问：阴影部分可以用哪个分数表示？为什么？折一折。

出示纸条3：

问：阴影部分可以用哪个分数表示？为什么？折一折。

四、要在学生的“整体生长”处设疑

“整体生长”是基于“联系的观点”，这里的联系不仅指数学与外部世界的联系，也指不同数学概念、不同数学结论乃至不同数学理论之间的联系。学生需要在认识、理解知识的本质及相互间的联系的基础上，形成良好的认识结构，优化数学在大脑中的组织形式，使学生的思维全面、灵活、深入，从而提高数学素养。

例如异分母分数加减法的教学中，教师出示：59+48=107，要探索的、有价值的问题情境，学生探究兴趣也被充分调动起来，从而给思维以动力，自然就积极主动地投入到学习新知的过程中去了。可见，精心设计的问题情境，是促使学生建构良好认知结构的推动力，是激发学生探究兴趣的重要措施，也是生成智慧的前提条件。

这些数的计算有什么相同点呢？学生通过观察、比较、分析、归纳出整数、小数、分数的计算实则都是相同的几个计数单位的加或减。

教师从知识整体出发，用联系的观点指导教学，在知识的连接处，在知识的从属、对立、统一关系中，采用整体教学手段，把合理的知识结构及时呈现给学生，帮助学生理清各部分知识的脉络及其在知识块中的地位和作用，把大纲中“学会”这一目标具体化、系统化，使学生所学的知识不是几个孤立的点，而是前后响应、浑然一体的有机整体，从而促使学生形成良好的认识结构，逐步具有“从整体看事物”的数学思想，培养有条理地思考和处理问题的能力。

学生的数学素养不是先天所具有的，也不是教师直接给予的，而是借助具体的问题情境，在问题的实践中逐步培养出来的。因此，我们要创设切合实际的问题情境，给学生一些权利，让他们自己去选择。