引导多思深思 提高数学思维素质
蔡永康
(石狮市第一中学,福建 石狮 362 70 0)
心理学家吉乐福特把创新能力解析为六个主要成份,即敏感性、流畅性、灵活性、洞察性、再定义性、独创性。这六大成份,无一不与思维素质密切相关;而思维素质的训练,总离不开思维广度的拓展与思维深度的开掘。从这个意义上来说,充分利用教材,引导学生多思广思,在思维训练过程中不断提高思维素质,以求达成创新能力的培养,这是素质教育的呼唤,是每个教育教学工作者所应负的重要使命。对此,文章仅取“一题多思”和“一题深思”的角度作狭义例析。
一、一题多思,激活思维,培养思维的敏感性、流畅性和灵活性
思维的敏感性、流畅性、灵活性,即指容易接受新事物,发现新问题;思维敏捷、反应迅速、对特定的问题情境能顺利产生多种反应或提出多种答案;具有较强的应变能力和适应性,具有灵活改变定向的能力。
在课堂教学中,结合具体问题情境,不失时机地引导学生从多角度、多层次去观察、分析问题,有意识地寻求多种途径去探讨同一问题,在熟练掌握常规方法的基础上力求创新,有所突破,将有助于提高思维的敏感性、流畅性和灵活性。
题一:求sin210°+cos240°+sin10°·cos40°的值。
一般思路:从局部观察,式中有3个二次三角式,都可利用三角公式变为一次式,接着再经过合并和变形转化,就解决了问题,即:

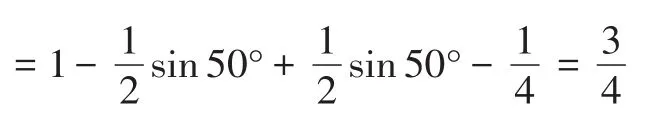
这种解法,只是按常规的降维思维,经过和差化积、积化和差的相互变换实现求解目的。这是一般层次的教学。
高一些层次,即着眼于思维能力得到进一步训练的教学,则应当充分利用现有教材的题例,引导学生变换观察和思维角度,鼓励多思,尽可能挖掘教材内在的思维训练因素,使教学情境呈现多元化的思维图象。分析如下:
事实上:

其中,式①有可视为勾股定理的结构,式②有可视为余弦定理的结构。这就拓宽了我们的解题思路,由此生发出多种解题方案:
[方案一]利用勾股定理的特殊结构和题中隐含的特殊角的关40°-10°=30°系进行变形转化,可得到下面解法:
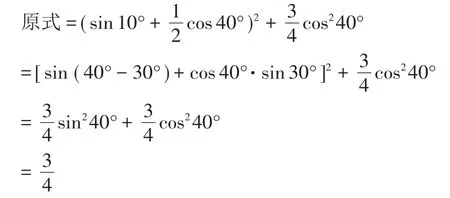
[方案二]利用余弦定理的特殊结构进行转化,可得:
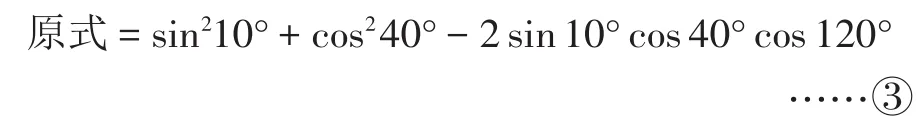
这实际上就在无形中产生了将学生思维从“数”向“形”转化的可能,由此改变了思维的方向。我们可以从形的角度去思考,激活学生的思维,诱发他们的探求的欲望。
作 出 三 角 形ABC,使AC=sin10°,BC=cos40°,∠ACD=120°
可以看到:

图1

图2
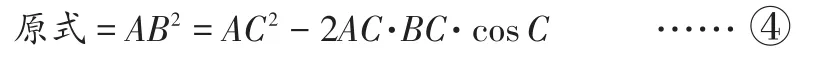
这就实现了数形的转化。但从“形”上仍不能看出原式的值是多少,若将③④式进行对比,促进学生把正弦定理代入④,得到另一个三角函数式:
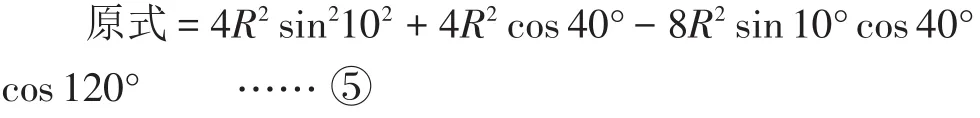
为了消除⑤③的差异,不妨作出三角形ABC的外接圆,设外接圆直径CD=1,(如图2),从而易知AB=sin120°。

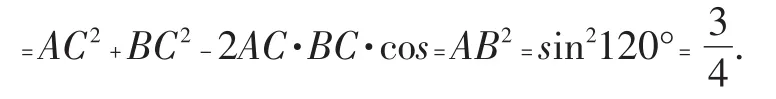
上述过程,概括地说,是一个由数而形,由形获值,多次发散,由浅入深的思维训练过程。我们还可以继续推进:
反思“方案二”的解题思路及所产生的结论,注意到cos40°=sin50°,于是③式可化为sin210°+sin250°-2sin10°sin50°cos120°=sin120°……⑥(这是图1中所涉及量价的关系式,是对图1内在边角关系的具体描述),实质上就是余弦定理的三角形式:sin2C=sin2A+sin2B-2sinA·sinB·cosC教学过程至此,学生将豁然领悟,顿足而呼:“早知直接运用这个余弦定理的三角式,问题不就迎刃而解了吗?”
的确,利用余弦定理三角式,可以获得如式⑥那样简捷优美的解法,简化了整个“方案二”的思维过程;而“方案二”的教学过程功不可没,它深化了学生对余弦定理三角式的认识,进一步完善了学生的认知结构,顿时使课堂充满了活力和激情,灵感的火花达到一触即发的境界。
于是,教师因势利导,让学生再从图2去观察获取:不但在三角形ABC中应用余弦定理可求AB2,在三角形ABC中运用余弦定理同样可以求得AB2。
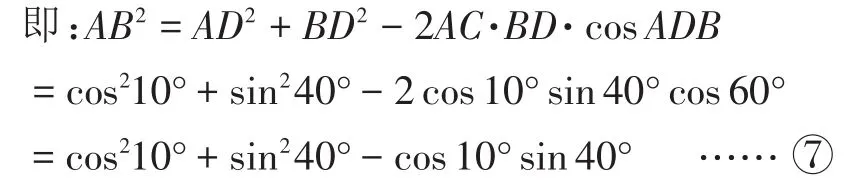
观察原式与⑦式,不难发现这两个式子是“一对”对偶式。于是,利用配对法又开始了新的认知:

这样,学生从中享受到一题多思的乐趣,从而产生新的更高的学习要求,教学中的思维训练有了良好的动机背景。
上述教例展示了这样一个事实:不失时机地引导一题多思,即通过对题目的特征、解题的思路、问题的结论等进行观察、联想、试验,不断调整观察、思考的角度、方式,以新的观点去看待思考的对象,分析解决所研究的问题,可以事半功倍地开发学生固有的、潜在的解题智慧,培养学生敏感、流畅、灵活的思维品质。
二、一题深思,推进思维,培养思维的洞察性、再定义性和独创性
洞察性、再定义性和独创性是在一般思维素质的基础上发展起来的,是思维不断深刻而产生质的飞跃的结晶。在教学过程中,教师应精心设计问题情境和教学方法,引导学生开展类比、对比、分析、归纳、联想等一系列思维活动,鼓励他们大胆提出教学猜想和创见,使学生不断获取“独创”的“成果”,将有利于提高创造性思维能力。
题二:已知a>b>c>0,求证
对这一习题,学生首先想到的是左边通分,然后证明分子、分母都小于零,这种解法比较繁琐。高中学生正处于思维发展时期,一般地说他们不会满足于这样就能解题结束了。教师利用学生的这种求异求精心理,可以因势利导引出:
思考一:能否设法将尽可能多的分母化成单项式,以简化运算过程?学生解题方案如示:
求异求精实质在于创新。当学生对上述证法获取一定的感性认识时,教师可进一步推出——
思考二:能否直接利用a-b,a-c,b-c的关系直接证明呢?学生通过直觉思维易于发现:a-b>bc>0从而得出:
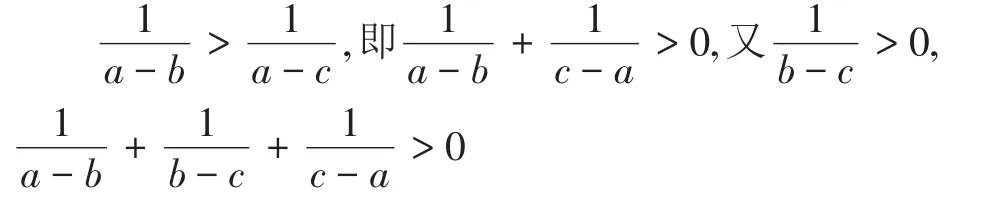
即证。
观察和探索是知觉和思维相互渗透的复杂的认知活动,不断地将观察到的事物和已知或假说进行联系思考,就易于发现新线索。到此教师可以引导学生作更深一层的思考。
设a>b>c,是否存在最大的正数K,使恒成立?如果存在,求出正数的最大值;如果不存在,请说明理由。分析如下:因为a-c>0,所以原不等式等价于通过类比,联想到基本不等式:对于是有:
[(a-b)+(b-c)]这 里 ,ab>0,b-c>0)当月仅当a+c=2b时等号成立,所以原不等式恒成立的实数K的最大值是4。
思维的深刻度达到一定程度时,就能见人所未见,发人所未发,情境如下:
这则教例给我们树立了一种信心:洞察能力、再定义能力、独创能力,并非什么神秘莫测的东西,更不是专属高智商人群所独有的心智现象;同样,培养学生思维的洞察性、再定义性和独创性,也并非高不可攀的目标,即使不依托专门的先进教材背景,依然可以有所作为。只要能充分利用现有教材,善于发掘教材的潜在功能,敢于并善于在教材题例的变形、解题途径的开辟、求解结论的引申、联想激情的调动等方面提出大胆积极的假想,并附之富有深究性和激励性的教学试验,那么,在数学教学中实现这思维“三性”的培养,便不是可望而不可及的。

