基于蝙蝠算法的成对载波多址信号盲分离算法
彭 闯,杨晓静,蔡晓霞
(国防科技大学电子对抗学院,安徽 合肥 230037)
0 引言
成对载波多址(Paired Carrier Multiple Access,PCMA)复用技术,1998年由ViaSat公司的Mark Dankberg提出,是一种能够有效提高卫星通信容量的新技术。该技术允许通信双方在同一频点发送两路相同调制方式的信号,而后通信双方均接收到相同的混叠后的信号,具有节省带宽资源、保密性强的特点[1-2]。在协作通信时,由于双方都已知本身的发送序列,并使用自身序列与混合序列相抵消,即可以得到另一方所发送的信息序列。而在非协作通信时,作为第三方接收到混叠后的信号,在没有任何先验信息的条件下,不能简单地通过合作通信的方法获得有用信号。同时下行混合信号由两路上行信号经过固定模式混叠而成,因此,不能通过多终端天线接收信号实现由欠定信号模式到正定信号模式的转变。
针对PCMA信号单通道接收的特点及在PCMA信号盲分离算法中出现的问题,文献[3]首先提出了使用独立分量分析解决PCMA信号分离的方法,但该方法着眼于协作通信。文献[4]中利用一种非负矩阵分解,给出了快速有效的盲信号分离算法,但对PCMA信号适用度不高。文献[5]提出了一种基于PSP算法及Kalman的盲分离算法,没有分析参数变化的影响。文献[6]提出了一种基于Gibbs采样算法的单通道盲分离算法,降低了复杂度,但未考虑频率偏移对算法的影响。文献[7]提出了一种基于编码辅助及过采样的PCMA盲分离算法,有效降低了误码率,但是过程复杂。文献[8]在对不确定环境序列估计的PSP算法基础上,提出基于SOVA-PSP算法的单通道盲分离算法,其性能与基于粒子滤波的算法相当,但文章主要讨论盲解调,对盲分离问题研究不足。文献[9]提出了一种基于信号重构及FastICA的算法,但该算法对信号频率偏移十分敏感,在信号频偏稍大时,分离性能明显下降。
可见,现有对PCMA信号的盲分离算法存在应用范围受限、复杂度高等缺陷。本文针对以上问题,提出了基于蝙蝠算法的成对载波多址信号盲分离算法。
1 PCMA信号盲分离问题的描述
PCMA复用技术在卫星通信链路示意图如图1所示[10]。

图1 PCMA信号通信链路示意图Fig.1 Schematic diagram of PCMA signal communication link
由图1可以看出,每一个地面基站发送一个上行信号,同时接收到由本地信号和另一地面基站发送的上行信号混叠而成的下行混合信号。由于两个地面基站发送的上行信号有几近相同的带宽和中心频率,符号的传输速率及基带数字调制方式也相同,因此盲分离困难,具有抗侦查能力强的特点。PCMA接收的复基带信号模型可以表示为:
y(t)=y1+y2+n
(1)

2 蝙蝠算法盲分离模型
本章对PCMA信号模型进一步分析,对算法中的信号正交分解及混合信号矩阵的重建进行理论推导,详细研究了蝙蝠算法寻优过程,提出了基于蝙蝠算法的PCMA信号盲分离算法。
2.1 信号模型
为进一步对PCMA信号模型进行描述,式(1)中两路上行信号可表示为:
(2)
(3)
式(2)和式(3)中,h1、h2分别表示接收信号中两信道的瞬时幅度,Δf1、Δf2和Δφ1、Δφ2分别表示两个信号分量的瞬时频率偏移和相位偏移。an、bn是相互独立的两个地面基站传输的信号符号序列,其取值与基带数字的调制方式有关,g1、g2是等效的脉冲成型滤波器的冲激响应。这里假设两个都是滚降系数为α的升余弦滤波器的冲激响应,对信号进行过采样的采样率为m的符号率。由于信号分量是循环周期为T的循环平稳过程,所以采样后信号成为周期为m的循环平稳随机序列。
2.2 信号的正交分解
对信号载波进行估计并将信号正交分解是本文算法的第一步。PCMA信号由两路上行信号混叠而成,正交分解可将一路混合信号扩展成两路信号,信号模型如下:
(4)
(5)

(6)
对于式中的两个分量,继续推导有:
(7)
相应地,混叠信号乘以正弦信号可以得到
(8)
2.3 重建观测信号矩阵
由于使用独立性判据“峭度”作为适应度函数,必须满足独立分量分析的条件,即观测信号数目大于等于源信号数目。所以本文利用正交分解后的两路信号重建混合观测矩阵。对式(16)中的信号通过低通滤波器,滤除掉高频分量,得到两路处理后的信号ya1、ya2,以满足“峭度”的分析条件。具体过程如下:
(9)

(10)
等价于:ya=h·s,其中h为观测信号的混合矩阵,s等价于源基带信号。
通过上述分析可以看出,当两路上行信号分量载频的平均值相差不多且对混叠信号载频估计精度较高时,上述推导能够完成一路混合信号到两路混合基带信号的转换,实现了将单通道欠定盲源分离问题转换为正定盲源分离问题。
2.4 基于蝙蝠算法的盲源分离算法
2.4.1蝙蝠算法
蝙蝠算法(Bat Algorithm, BA)是剑桥大学学者Yang于2010年基于群体智能提出的启发式搜索算法[11-12],是一种搜索全局最优解的有效方法。本文根据该算法的仿生学原理将种群数量为N的蝙蝠个体映射为D维空间中的N个可行的混合矩阵,把蝙蝠的飞行和搜寻猎物的过程作为算法的解混优化过程,求解蝙蝠个体的“峭度”作为适应度函数来衡量蝙蝠个体所的解混矩阵效果,优化和搜索过程中好的可行解替代较差的可行解的迭代过程模拟乘蝙蝠群体中的优胜劣汰。
2.4.2算法推导
根据蝙蝠的回声定位行为方式及其与优化目标的相关联性,本文将种群数量为N的蝙蝠个体映射在与数据长度相同的D维空间中,蝙蝠个体的频率、速度、位置、响度及脉冲速率的表达式是本节研究的重点。

(11)
式(11)中,fi为蝙蝠i在搜寻猎物时使用的脉冲频率,fi∈[fmin,fmax]为搜索脉冲频率范围,β∈[0,1]是来自均匀分布的随机变量,x*是N只蝙蝠中的全局最优解。
通过对当前最优解随机游走的方式实现局部搜索,具体方式如下:
xnew=xold+εAt
(12)
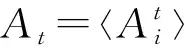
蝙蝠依靠脉冲来确定猎物位置,算法中脉冲响度及脉冲发射速率的改变决定了算法的寻优效率。因此响度和脉冲发射率的变化如下:
(13)
式(13)中,0<α<1和γ>0是常数,本文中设α=0.5,γ=0.9。可以看出随着t→,有A→0及r→r0。符合蝙蝠接近目标时,提高脉冲发射速率、降低脉冲响度的生物学机理。
2.4.3适应度函数及初始群体选择
本文采用两路信号“峭度”的绝对值之和作为适应度函数,与K-L散度、互信息和负熵等独立性判据相比更为简单明了。即:
(14)
对蝙蝠个体进行零中心化及白化预处理后[14],fitness(yi)越大,表明该蝙蝠个体的各分量间的独立性越强,即分离矩阵h有更好的分离效果。
考虑到若两路分量信号是不同种类的信号,可能既有超高斯信号又有亚高斯信号,此时仅使用“峭度”无法分离。因此本文提出采用“峭度”的绝对值作为适应度函数和信号独立性的判据。仿真结果表明“峭度”的绝对值作为适应度函数能够有效地实现PCMA信号的盲分离,解决了仅用“峭度”无法有效区分超高斯信号、亚高斯信号的问题。
初始群体是通过随机方式产生由若干个分离矩阵构成。盲源信号分离中运算量由分离矩阵大小决定。根据PCMA信号特点,设群体规模为50个随机矩阵,即50只蝙蝠个体进行寻优即可。
2.4.4蝙蝠更新规则
蝙蝠更新包括蝙蝠个体更新和群体最优蝙蝠更新[15]。蝙蝠在多维空间中不断飞行,位置、速度的更新保证蝙蝠能够尽可能地对周围空间进行探索,实现了算法的全局寻优能力。最优蝙蝠会在原位置附近进行随机飞行,试探是否有局部更优解,保证了算法的局部寻优能力。在盲分离算法中常用的FastICA算法是结合最速下降法和牛顿迭代法所实现的,对初值较为敏感,易陷入局部最优解。相比这些传统的盲分离算法,本文提出采用蝙蝠算法作用于PCMA信号盲分离中,解决了传统算法易陷入局部最优解的问题,从而实现了动态控制全局搜索和局部搜索之间的转换。
2.4.5算法流程
结合PCMA混叠信号的特点,本文提出的基于蝙蝠算法的盲源分离算法流程如下:

2)计算初始每只蝙蝠适应度fitness(i),并计算出当前种群内最好解x*及其适应度函数值peak_value,i=1,2,…,N;
3)判断是否达到算法最大迭代次数Max_gen,若满足,输出为最优解。若不满足,则转入4);
5)产生一个随机数rand1∈[0,1],若rand1>ri,则在当前群体最优解xold的位置进行随机扰动,通过式(12)得到一个新的解xnew。
6)产生一个随机数rand2∈[0,1],若rand2
7)更新蝙蝠群体解集,找到当前最优解x*,转到3)。
整体算法模型如图2所示。
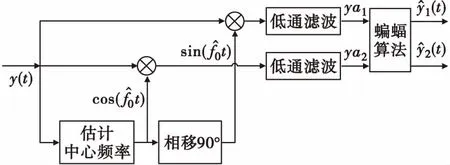
图2 算法模型Fig.2 Algorithm model
3 仿真实验
实验平台为64位WIN8操作系统,Intel Core i5-3337U CPU,1.80 GHz,内存4 GB的PC机,仿真软件采用R2014b版Matlab。
为了检测算法分离效果,引入相似系数作为衡量盲分离算法性能的指标,其定义如下:
(15)
信噪比和频率偏移是对分离效果产生影响的两个重要因素。因此通过实验一、实验二,检验其对本算法分离效果的影响,并与使用FastICA算法的分离效果进行比较。
设PCMA信号的两路上行BPSK信号为y1(t)、y2(t),升余弦成型滤波器的滚降系数分别为0.3和0.4,载波频率为f1=f2=150 kHz,抽样频率fs=1 500 kHz。符号速率rb=12.5 Kb/s,每个符号周期内的样本数为N=2 048,通过高斯白噪声信道,过采样率m=10,采样后通过低通滤波器,低通滤波器带宽与信号带宽相同,滤除信号频带外干扰,得采样序列y(l)。
采用传统的信号二阶循环累积量对信号进行载频估计。对采样序列y(l)求二阶循环累积量循环谱如下图3所示。
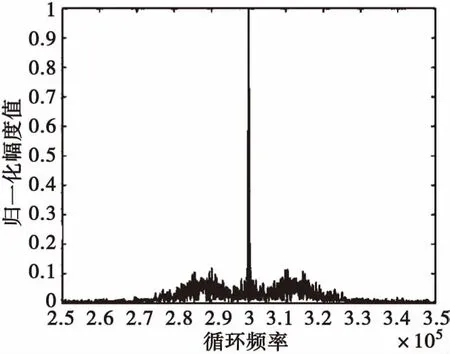
图3 信号的二阶循环累计谱Fig.3 Two order cyclic cumulative spectrum of signals
由图3可以看出循环累计谱在3×105处出现峰值,结合PCMA信号特点可知,出现循环谱峰值处的循环频率即为载波频率的2倍。可求得两路上行信号载波频率为f1=f2=150 kHz。
实验一 信噪比对分离效果的影响
设PCMA系统固定频率偏移分别为Δf1T=10-2和Δf2T=-10-2,加入随时间变化的相位偏移随机量,其随机量不大于频率偏移的10%,相位偏移为Δφ1=-Δφ2=10-4。

仿真结果如图4和图5,其中图4为FastICA算法分离性能,图5为本文算法分离性能。可以看出在频率偏移10-2数量级时,两种算法的分离性能都随着信噪比的增大而上升,但本文算法在信噪比低于5 dB时,相似系数更大,分离效果更好。比如,在信噪比为-5 dB时,利用FastICA算法得到的两路信号与源基带信号相似系数分别为0.75,0.79而相同条件下使用本文算法得到的相似系数为0.84,0.86。
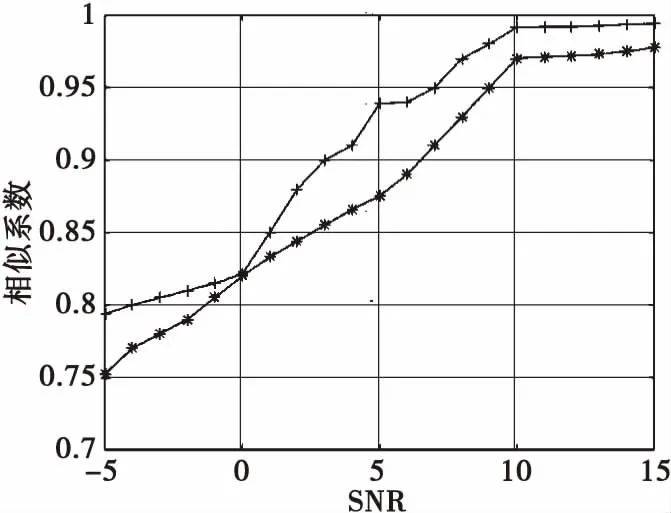
图4 FastICA算法的分离性能图Fig.4 Separation performance diagram of FastICA algorithm

图5 本文算法的分离性能图Fig.5 Separation diagram of the algorithm in this paper
该实验说明在低信噪比的条件下,本文算法相比于文献[9]使用的FastICA算法具有更好的分离性能。
实验二 频率偏移对分离效果的影响及算法收敛性研究
设固定信噪比为10 dB,对第一路上行信号频率偏移Δf1T分别取1×10-1、5×10-2、1×10-2、5×10-3、1×10-3,第二路上行信号频率偏移Δf2T=-Δf1T,相位偏移为Δφ1=-Δφ2=10-4。对每个实验点进行100次蒙特卡洛实验。实验结果见表1。
表1给出了不同频率偏移条件下,两种算法的相似系数的变化。可以看出,随频偏的减小,两种算法的相似系数增加,分离性能提高。但在频偏较大时,本文算法得到的相似系数大于FastICA算法,因此具有更好的分离性能。比如,在Δf1T=-Δf2T=5×10-2时,FastICA算法的相似系数分别为0.71,0.68而相同条件下本文算法得到的相似系数为0.85,0.84。说明在信噪比固定,本文算法相比于文献[9]使用的FastICA算法受频率偏移影响更小,有更好的分离性能。

表1 两种算法分离效果比较Tab.1 Comparison of separation effects between the two algorithms
在实验二基础上对算法收敛性进行研究,选取频率偏移Δf1T为1×10-2,迭代次数为200次,分离所得两路信号相似系数均值与迭代次数关系如下图6所示。

图6 两种算法收敛性比较Fig.6 Comparison of the convergence of two algorithms
由图6可以看出随迭代次数增加,两种算法收敛速度差别不大,但蝙蝠算法所得相似系数增长更快,相似程度更高。算法收敛性是制约其在盲源分离中应用的重要因素,本实验证明了蝙蝠算法在盲源分离中的优越性。
4 结论
本文提出了基于蝙蝠算法的成对载波多址信号盲分离算法。该算法首先对接收到的PCMA信号进行正交分解,处理得到两路基带混合信号,利用独立性判据“峭度”作为适应度函数,使用蝙蝠算法实现源基带信号分离。仿真实验表明,该算法具有良好的分离性能且复杂度低并对频率偏移不敏感的特点。

