基于攻角修正系数的落点预测方法

杨小会，王 超，薛 冰

(机电动态控制重点实验室，陕西 西安 710065)

0 引言

弹道修正引信是集成有传统引信功能和弹道修正功能的新型引信[1]，能显著提高中大口径系列榴弹的打击效能和效费比[2]，是大量库存弹药精确打击改造的重要途径。落点预测是弹道修正技术的关键技术之一，其精度和实时性直接影响弹道修正的效果[3]。采用卫星定位进行弹道测量，利用当前弹道参数结合理想的弹道模型外推实际落点是一种常用的方法[4]。

落点预测通常采用的弹道模型有六自由度模型、四自由度模型及质点模型三种。六自由度弹道模型精度高，但是需要测量弹道参数和弹丸姿态参数，模型复杂，计算量大，对硬件要求较高[5]。三自由度的质点弹道模型简单，计算量少，但其仅在射程较小或弹道末段效果好[6]。四自由度弹道模型仅需要测量弹道参数，计算量少[7]，但由于其无需测量弹丸姿态，攻角仅用角运动方程的解析解直接算出，加之弹道修正过程中攻角变化剧烈，因此解算精度不高，影响落点预测精度。针对四自由度模型中攻角解算精度不高引起落点预测精度低的问题，本文提出了基于攻角修正系数的落点预测方法。

1 攻角对落点预测精度的影响

以155 mm底凹弹为平台，初速930 m/s，射角51°，采用双旋弹道模型和四自由度弹道模型解算弹道，两种模型解算的弹丸攻角随时间变化见图1，同一时刻攻角的比值即攻角修正系数见图2。

图1 弹丸攻角Fig.1 Attack angle of projectile

图2 攻角修正系数Fig.2 Modified coefficient of attack angle

由图1可以看出，四自由度弹道模型和双旋弹道模型解算的攻角相差较大，会导致攻角诱导阻力和马格努斯力与真值相差较大，进而影响射距和横偏的预测精度。

在不引入任何误差的条件下，不同预测时刻四自由度弹道模型落点预测误差见图3。采用图2的攻角修正系数修正四自由度弹道模型攻角进行预测落点，预测误差见图4。通过图3和图4误差对比可见，采用修正系数修正攻角同时降低了射距误差和横偏误差，60 s后落点预测误差绝对值小于20 m，提高了落点预测的精度。

图3 四自由度弹道模型落点预测误差Fig.3 IPP error without modified attack angle

图4 采用修正后攻角不同时刻落点预测误差Fig.4 IPP error with modified attack angle

2 基于攻角修正系数的落点预测方法

2.1 攻角修正系数获取方法

四自由度弹道模型落点预测误差不单是攻角解算误差，还包含弹道气象散布、弹丸偏心、弹丸的质量及气动散布等因素引起的误差。这些误差都会影响攻角的计算精度，表现为攻角修正系数值产生波动，可通过卡尔曼滤波获取攻角修正系数的最优估值，进而减弱这些误差对落点预测精度的影响。

滤波的状态方程选择为四自由度弹道模型，其为多变量非线性方程，需采用非线性滤波。非线性滤波器中常用的是扩展卡尔曼滤波器，其首先利用泰勒级数将非线性方程展开，通过一阶线性方程近似原有非线性方程，根据弹道测量模块的观测值，获取弹道参数及攻角修正系数的最优估计值。

2.1.1状态变量及状态方程

滤波的状态变量选择为位置、速度、转速及攻角修正系数8个，对应的状态方程采用引入攻角修正系数的四自由度弹道模型，由图2可知，攻角修正系数近似为常值，因此攻角修正系数的模型选为常值函数，如式(1)所示。

状态方程：

(1)

cx0、cxα2分别表示零升阻力系数和诱导阻力系数，cy、cz和clp分别表示升力系数导数、马格努斯力系数导数和极阻尼力矩系数导数；m、d、s和Jx分别表示弹丸质量、弹径、弹丸参考面积和极转动惯量；ρ表示空气密度；Q表示模型噪声。

αe表示攻角，计算公式见式(2)。

(2)

2.1.2量测变量及量测方程

滤波的量变量选择为卫星定位测量的发射系位置、速度信息，磁传感器测量的转速信息共7个，对应的量测方程如公式(3)所示。

(3)

式(3)中，R表示量测噪声，量测转移矩阵

2.2 基于攻角修正系数的落点预测方法

采用扩展卡尔曼滤波估计的弹道位置、速度，弹丸转速及攻角修正系数作为弹道初始诸元，解算引入攻角修正系数的四自由度弹道模型，见公式(4)。

(4)

采用滤波估计的攻角修正系数见图5，可以看出，对于确定的某发弹丸，攻角修正系数近似为某一常值，因此引入的攻角修正系数可通过采用一段时间内的滤波均值kαE进一步提高预测精度。

图5 滤波估计攻角修正系数Fig.5 Estimate results of modified coefficient

通过卡尔曼滤波估计弹丸真实攻角与弹道模型解算攻角的修正系数，修正攻角进行落点预测，不仅可以减少由于攻角解算精度不高带来的预测误差，同时还可以减少由于弹道气象、弹丸偏心、弹丸的质量及气动散布等因素引起的落点预测误差，能有效提高落点预测精度。

3 仿真和外场试验验证

以155 mm底排弹为平台，分别采用仿真数据和外场试验雷达弹道测量数据验证基于攻角修正系数的落点预测精度。

3.1 仿真验证

以155 mm底排弹为平台，在初速933 m/s，射角52°(射程约36 km)，标准气象条件下，考虑初速、射角、射向等射击误差，弹丸阻力、升力、质量、偏心、底排等气动和弹丸固有误差，气压、虚温和弹道风等气象测量误差，解算双旋弹道模型，采用蒙特-卡洛仿真方法生成一组纵向准确度误差5‰X，纵向密集度1/240，横向准确度误差2.5 mil，横向密集度1 mil的无控弹道。

在这组无控弹道的基础上考虑卫星定位位置误差10 m(1σ)，速度误差0.5 m/s(1σ)，转速测量误差1‰(1σ)，采用基于攻角修正系数的落点预测算法预测弹丸落点，将预测的落点坐标与仿真的无控弹落点坐标进行比较，计算落点预测误差，统计落点预测的CEP。图6为300次蒙特-卡洛仿真结果，由图可看出预测CEP为20.3 m。

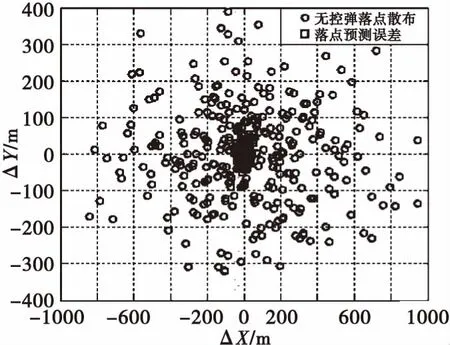
图6 蒙特-卡洛仿真结果Fig.6 Simulation results of IPP

3.2 外场试验验证

基于155 mm底排弹全装药最大射程角(射程36 km)外场试验雷达跟踪数据，实测气象数据，采用基于攻角修正系数的落点预测算法预测弹丸落点，将预测的落点坐标与实测落点坐标进行比较，计算落点预测误差，将四发弹丸的横纵向预测误差进行统计，评估预测精度。

图7为不同时刻各弹丸的射距和横偏的预测误差，可以看出横纵向落点预测的绝对误差从出炮口后约70 s开始小于50 m，从90 s开始小于30 m。图8为采用修正系数修正攻角和不修正攻角两种落点预测方法不同时刻四发弹丸落点预测精度，可以看出采用修正系数修正攻角能有效提高弹丸落点预测精度，其落点预测CEP从70 s开始小于50 m，从85 s开始小于30 m，最终CEP可优于20 m。

图7 不同时刻各弹丸的射距和横偏的预测误差Fig.7 Down range and cross range IPP error

图8 不同时刻四发弹丸落点预测精度Fig.8 IPP CEP

4 结论

本文提出了基于攻角修正系数的落点预测方法。该方法以引入攻角修正系数的四自由度弹道模型为状态模型，卫星定位测量的位置、速度和磁传感器测量的转速为量测量构筑量测方程，采用扩展卡尔曼滤波估计攻角修正系数，然后基于攻角修正系数解算四自由度弹道模型预测弹丸落点。155 mm底排弹最大射程仿真和外场试验数据验证结果表明，采用修正系数修正攻角预测落点能有效提高弹丸落点预测精度，预测CEP可优于20 m，可推广应用于中大口径系列榴弹。