基于实时信息的公交运行速度控制策略与算法研究

严 海，刘润坤

(北京工业大学交通工程北京市重点实验室，北京100124)

0 引言

通过以往的研究发现，运行的可靠性是影响常规公交吸引力的一个重要因素.常规公交随着运行距离的增加，其受道路交通运行的影响会累积增加，可靠性会进一步降低[1].这一影响表现在区间速度不稳定、停站时长的变化等，常规公交的到站延误会导致“串车”现象，这是公交运行时间不可靠的主要表现.

Newell在1964年第1次解释了该现象发生的原因，之后学者们对针对“串车”现象进行了一系列的研究，希望通过减少“串车”的发生来改善公交的运行可靠性.相应的控制策略分为静态控制和实时控制.刘环宇认为以往的研究中对于公交车辆时刻表的优化设计，大多没有考虑公交系统的可靠性因素.Ceder，Palma和Dong建立了基于可靠性的公交时刻表优化模型，将可靠性作为约束条件，优化目标仍为社会福利最大.Jiamin Zhao提出了一个最优化松弛时间的模型，以增加公交系统时间表的稳定性，当松弛时间足够大的时候，可以提高公交运行的可靠性[2].但是Newell，Carlos F.Daganzo[3]认为：因为受到如交通拥堵、交通事故等的影响，即使考虑到较大的时间松弛，也不能够总保持时刻表的按时执行.因此，研究如何根据实时的公交车头时距采取动态调节，提高公交运行可靠性成为学者们探讨的话题.

动态调节主要可以分为站点控制和站间控制.站点控制的基本思路是选择合适的控制点并确定在控制点的停车时长.Turnquist和Blume提出控制点应当设在公交车车头时距差异较大的站点，结果表明该方法可以减少乘客的等待和出行时间.Rufi构建仿真模型分析控制点设置位置，结果表明，最好的控制点可以有效提高可靠性，但如果控制点位置设置欠妥，则比不实施效果更差.Carlos F.Daganzo[3],Bartholdi J.J.[4],Simon J.Berrebi[5]提出基于实时数据的控制点控制策略，结果表明考虑实时信息可以减少控制时间，并且减少乘客等待时间.而当只有一个控制点的时候，不能够有效的保证公交服务的可靠性.Carlos F.Daganzo[3]，Chen Q.[6],Simon J.Berrebi[5]通过对比以往的站点控制策略发现，基于时刻表的控制对于车头时距的稳定性并无明显的提高；即使在多个控制点的情况下，仍是如此；而基于车头时距的控制，虽然可以提高车头时距的稳定性，但需要更长的控制时间.

Chandrasekar[7]提出控制公交行车速度的方法，认为速度控制是乘客容易接受的一种控制策略.Daganzo[8]通过考虑到前车和后车的实时间距来调整车辆的速度，使车辆间保持一个稳定的车头时距.

综上，站点控制虽然能够在一定程度上提高公交运行的可靠性，但是对于线路较多的中途站，这种控制对于道路交通流影响较大，也不易被乘客接受.而以往对于速度控制的研究中，案例的设计及乘客到达率的动态变化未能很好的结合实际公交运行情况，模型与实际情况相差较大，并且对于速度控制策略的应用场景、乘客的候车时间、稳定性效果的改善结果等分析较少.

基于上述的研究分析，本文提出一种基于常规公交实时信息的车辆速度控制方法，来研究公交运行可靠性问题.并通过数值仿真验证算法的有效性，然后对结果进行评价与分析.

1 可靠性的定义和模型的构建

公交运行的可靠性有着不同的定义[3]，本文将公交运行的可靠性定义为，公交运行时能够保持一致的车头时距，即以期望的时间间隔到达每一个站点.

根据公交车的运行过程，将公交的运行时间分为站间的行程时间和站点停车时间，如图1所示.将连续2辆公交车在同一站点的出发时刻之差计为车头时距.

图1 公交行程时间分段示意图Fig.1 Bus travel time and time segmentation

根据上述公交运行过程建立数学模型，具体参数定义如表1所示.

表1 参数定义Table 1 Parameters definition

假设乘客的到达率服从均匀分布，式(1)可变形为

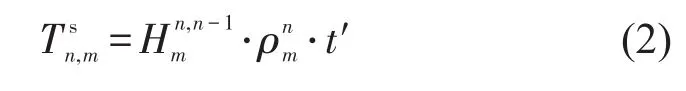
式(2)即为文献[3,9]研究中所提出的公交停车时间表达式.

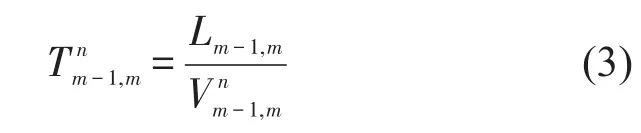
第n班车在m站的离站时刻可表示为公交车在m-1站的离站时刻加上在m-1和m两站间的行程时间与在m站的停车时间之和，即

2辆公交车在m站的车头时距为连续2辆公交车在m站的离站时刻之差，即

将式(2)～式(4)带入式(5)得到

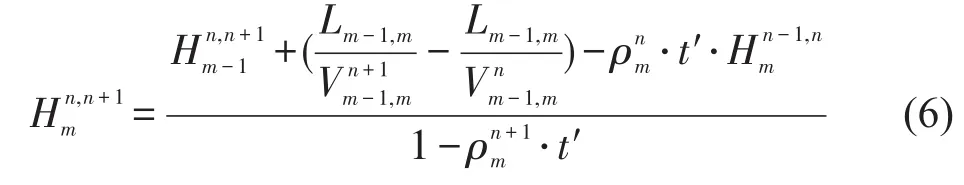
式中：min_station_gap为最小发车间隔；max_station_gap为最大发车间隔.

将式(6)带入式(7)得到

根据上述模型，设计能够实时计算期望运行速度的算法.所需数据为已知的公交车载记录仪实时上传的数据及线路属性数据.

算法如下：

Step 1记录第n+1班车从m-1站的发车时刻，计算第n，n+1班车在m-1站的车头时距.

Step 2根据历史数据查找第n班车在m-1站至m站的平均速度，第n班车及第n+1班车在m站的乘客到达率.

Step 3根据式(8)，计算期望行驶速度，并控制第n车以该期望速度在m-1站至m站间行驶.

Step 4判断是否到达最后1站，即m是否等于M，如果未到，则m=m+1，返回Step1；如果已到，则转到Step5.

Step 5判断是否已是最后1班车，即n是否等于N，如果不是，则n=n+1，返回Step1；如果是，则停止.

2 算例

2.1 场景设计

本文采用数值仿真的方法对模型进行求解和评价，设置3个场景，如表2所示.

2.2 基本参数设置

本文设置了1条设站11座，站点间隔500 m的公交线路；共模拟12班同向运行的常规公交车，始发站的发车间隔设为10 min，根据以往的研究将每个乘客的上车时间设为2 s.基本参数如表3所示.

本文模拟公交车运行时长约为10 000 s，由于道路交通流速度和每站乘客到达率在每一时刻都不同，为了进一步分析数据的时变特征，将分析时段设定为每10 min一段.

表2 场景说明Table 2 Scenarios description

表3 基本参数设置Table 3 Basic parameter settings

以往的研究表明，常规公交的站间平均运行速度大多在10～25 km/h，且线路运行时车速呈现“两头高中间低”的特征.因此本文模拟时参考这一特征，并在中途站间随机生成速度更低的数据，以模拟拥堵路段.共模拟了19个时段，190个道路交通流数据，如表4所示.

表4 道路交通流速度Table 4 The speed of road traffic flow (m/s)

乘客到达率依据现实数据特征模拟生成，规则为越靠近始发站的越高，越靠近终点站越低，并在中间站随机生成部分高值和低值站点，更好模拟乘客到达不均匀现象，如表5所示，共模拟了19个时段，209个到达率数据.

表5 乘客到达率Table 5 Passenger arrival rate (person/min)

对于场景1～3，分别进行计算，如表6所示.

表6 3种场景的计算过程Table 6 The calculation process of three scenarios

3种场景下的仿真流程图如图2所示.

本文的算法及数值仿真采用Python2.7.13进行编程实现，计算部分使用到了scipy包中的最优化计算方法.通过计算，可以得到3种场景下的车辆运行状态数据，进而可以通过对相关参数的评价，来验证实时信息下公交速度控制策略的效果.

3 结果分析与评价

3.1 车头时距稳定性

根据每班车在各站点的离站时刻绘制公交运行时空图，如图3所示.

由图3可以看出：场景1中，在某些站点会出现公交不均匀到达的现象，甚至出现串车的情况；场景2中，明显改善公交的不均匀到达现象；场景3中，速度控制虽然可以提高公交到站时间的稳定性，但是较场景2来说改善不明显，但避免了“串车”现象.

根据仿真模拟的行程时间记录，可进一步分析车头时距变化，如图4所示.

由图4可以看出：场景1中，公交车的车头时距波动较大；场景2中，车头时距达到较优的状态，基本维持在600 s；场景3中，由于实际行驶速度不能达到期望速度，但车头时距的波动已经明显降低.进一步对比平均车头时距标准差，可以看出，采取速度控制后车头时距的稳定性有明显提高.场景2车头时距的标准差较场景1降低77.63%，较场景3降低29.05%.

图3 3种场景下公交运行时空图Fig.3 Time-space diagram of service time in three scenarios

3.2 公交运行可靠性

根据本文公交运行可靠性的定义，通过平均绝对误差可以评价公交车头时距与发车间隔时间的偏离程度，进而评估公交运行的可靠性.平均绝对误差计算公式如式(9)所示，结果如图5所示.

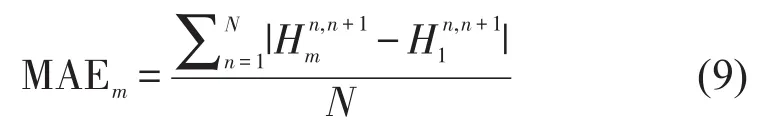
图4 3种场景下公交车头时距Fig.4 Bus headway in three scenarios

从图5可以看出，采取速度控制策略，不论是场景2还是场景3，车头时距与发车间隔的平均绝对误差均会减少，表明采取速度控制能有效提高公交运行的时间可靠性，较场景1分别提高93.5%、28.4%.并且，采取速度控制的方法对于长线路公交的运行时间可靠性的提高更明显.

图5 站点的车头时距平均绝对误差Fig.5 Mean absolute error of the bus headway in each station

3.3 乘客平均等待时间

乘客的平均等待时间与公交的车头时距的均值及标准差有关，即

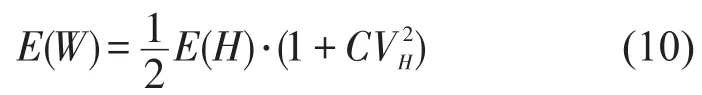
式中：E(W)为平均等车时间；E(H)为车头时距的均值；CVH为车头时距的标准偏差系数，等于车头时距的标准差除以均值[10].

计算得到乘客平均等待时间如图6所示.

图6 每一站的乘客平均等待时间Fig.6 Average waiting time for passengers in each station

从图6可以看出，乘客的平均等待时间随距离始发站的距离增大而增长.场景2的乘客平均等待时间最短；而场景3乘客平均等待时间有所增加，主要是由于提高公交运行的可靠性的同时，导致车头时距的均值增大12.7%，因此乘客等待时间也有所增长，增幅最大为8.7%.

由此可以看出，应用本文的算法，采用实时速度控制策略，在场景2下，效果最优；场景3下，尽管提高公交运行的可靠性但会略微增加乘客的平均等待时间，但增加的等待时间相对于可靠性的提高是可接受的.具体数据如表7所示.

3.4 公交运行速度

根据行程记录及算法的求解，可以得到3种场景下的实际行驶速度，如图7所示.

图7 3种场景下部分公交车的站间行驶速度Fig.7 The speed of bus between stations in three scenarios

表7 结果评价Table 7 Evaluation of results

从图7中可以看出，在某些路段中计算出的期望行驶速度低于不采用控制时的速度，这一现象表明，为了保证运行的可靠性，速度控制策略下，公交车的行驶速度在某些路段中会要求低于实际道路交通流的平均速度.也就意味着，在某些路段中公交无需以所能达到的最快速度行驶.

4 结论

本文讨论了实时的公交行驶速度控制策略和算法，通过实时速度控制策略，可以显著提高公交运行时间的可靠性，但是如果公交线路受道路交通流影响较大时，采取该策略后，乘客平均等待时间与总的行程时间均会增加.并且要维持公交运行时间的可靠性，公交车运行不需要在任两站间均保持所能达到的最高速度，其运行速度需结合实际情况，维持在一个合理的范围内.因此，如何实现公交运行的稳定性、乘客平均等待时间、行程时间三者的协同控制，是下一步的研究方向.