绿色多式联运随机优化策略

李 珺，杨 斌，朱小林

(上海海事大学物流科学与工程研究院，上海201306)

0 引言

伴随经济快速发展，单一的交通运输体系已难以满足市场需求，应不断提高不同运输方式的一体化衔接和协作水平，发展节能减排的多式联运业务，对于降低成本、减少环境污染具有重要意义.随着我国综合运输体系的建设与完善，多式联运有着广阔的发展前景，对多式联运的学术研究已成为热点，特别是绿色多式联运路径优化策略更是成为国内研究的焦点问题.

Assadipour等[1]为求解多式联运路径运输优化问题，建立一个运用启发式算法求解的双层双目标模型；Li L.等[2]将多式联运路径优化定制为集装箱流量控制问题；张运河等[3]提出求解多式联运最佳运输路线的广义最短路算法.Demir E.等[4]运用样本逼近方法优化时间和需求不确定时绿色多式联运路径；王雁凤等[5]探究运输过程中船舶、车辆的碳排放因素；Yang K.等[6]设计随机模糊方法，求解费用和时间混合不确定时多式联运路径优化问题；Meraklı M.等[7]采用线性混合整数规划方法建立两种多式联运鲁棒优化模型，求解需求不确定时路径优化的精确解；Wang X.等[8]研究了网络拓扑结构不确定时多式联运网络规划布局及路径优化问题.

现有的多式联运路径优化研究主要集中在绿色及不确定优化，但针对速度服从随机分布时绿色多式联运路径优化的研究甚少.本文的主要研究内容是在合理的样本规模下，当绿色多式联运网络中交通工具的行驶速度服从随机分布时，对运输路径及方式进行决策，以成本期望值为目标，构建绿色多式联运随机优化模型，借助样本平均近似方法，运用基于优先权的粒子群算法进行求解，通过设计多种情景进行模拟，得出较为理想的运力配置方案.

1 问题描述与建模

1.1 问题描述

速度服从随机分布时绿色多式联运路径优化策略是一个集成多种运输方式、多条运输路径、多个枢纽点、多种不同随机因素和固定起终点的复杂问题.由于公路交通状况复杂多变和海上天气等自然因素的未知，致使运输过程中交通工具的速度具有随机性，增加了网络的复杂性，通过构建多层、稳健的绿色多式联运网络，发挥可靠、柔性的网络效应，规划合理的优化策略.

为描述速度服从随机分布的绿色多式联运网络，设计由起点o，枢纽点i、j、k，终点d，o,d,i,j,k∈I，和水运α、公路β、铁路γ在内的3种运输方式组成多式联运网络图，如图1所示.不考虑因中转产生的费用.速度的随机性可使用样本平均近似方法，多次运行可产生不同速度样本的确定性优化模型.基于以上描述，构建绿色多式联运随机优化模型.

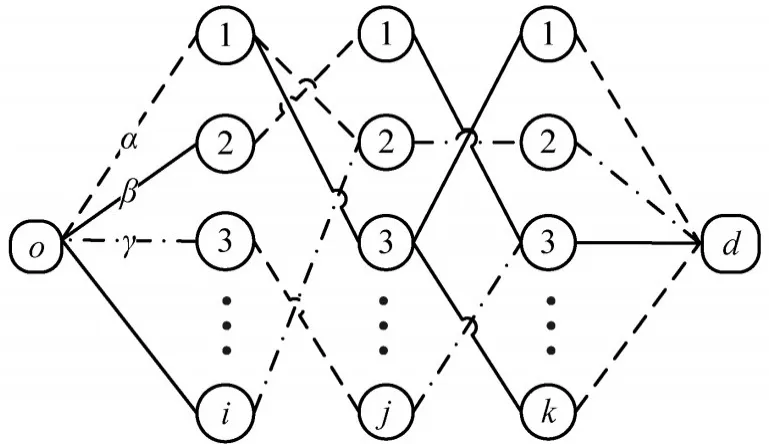
图1 多式联运网络图Fig.1 Multimodal transportation network diagram

1.2 模型构建

(1)符号说明.

I——节点集合，i,j,k∈I；

Z——运输方式集合，α为水路运输，β为公路运输，γ为铁路运输，α,β,γ∈Z；

cz——单位时间的运输费用；

ce——碳税税率，取10元/t；

dcj——客户需求量；

lj——节点处货物的中转集拼量；

capβ——卡车的容量限制；

n——极大数

r——运输时间约束；

cemax,cemin,cmax,cmin——碳排放和运输成本的最大值与最小值；

τ——碳排放成本系数；

ω——运输成本系数，τ+ω=1；

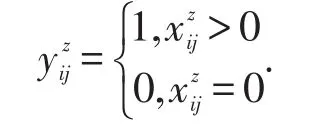
(2)目标函数.

式(1)和式(2)为碳排放成本及运输成本的期望值；式(3)和式(4)为碳排放成本和运输成本的具体表达式；式(5)～式(7)是两个成本的无量纲化，化双目标为单目标.

(3)约束条件.

式(8)为运输方式选择约束；式(9)为在中转点发生集拼时运量守恒约束；式(10)为客户需求应被满足；式(11)为运输能力约束；式(12)为运输时间约束；式(13)为决策变量的关系约束；式(14)和式(15)为决策变量约束.

(4)碳排放量计算公式.

船舶主机在实际航速下每小时的燃油消耗量为

单位时间船舶燃料燃烧产生碳排放量计算公式为

式中：MFv——船舶主机的燃油消耗；

MFvo——额定速度下船舶主机的燃油消耗量(t)；

ge——燃油消耗率(kg/kW⋅h)；

Neo——额定航速veo下船舶的主机功率(kW⋅h)；

Ne——实际速度vizj下船舶的主机功率(kW⋅h)；

coα——柴油燃料低位发热值(kJ/t)，取值42 652；

大型卡车行驶每百公里碳排放量计算公式为

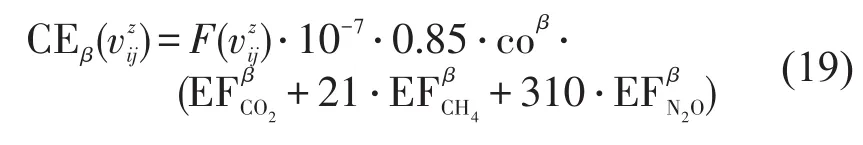
式中：coβ——汽油燃料低位发热值(kJ/kg)，取值为43 070；

单位距离内，火车每运送1 t货物所产生的碳排放因子为

2 求解算法

目前演化计算方法广泛用于解决约束优化问题，且被证明很有效.粒子群优化算法(PSO)是演化计算方法中的一种，是随机优化、非线性连续优化等问题的有效优化工具.同时，粒子群算法的解码和编码设计较为简单，有良好的可操作性.因此，采用基于优先权的粒子群算法对模型进行求解.

2.1 算法参数

s为粒子种群数；e为粒子的维度；r为粒子的搜索半径；c1，c2为学习因子；N为无穷小初值；t为约束因子；p为种群最大的迭代次数，p1为种群当前迭代次数；w为惯性权重，maxw，minw分别是粒子惯性权重的最大值和最小值，用以更新惯性权重，即maxw-p1⋅[(maxw-minw)/p].

表1 算法参数值Table 1 The value of algorithm parameter

2.2 基于优先权的粒子群算法步骤

Step 1初始化参数.

设定多式联运网络中速度的分布函数，给定样本规模、距离、耗油量及费用，计算对应样本规模的成本，在允许的范围内初始化种群的初始位置和速度.

Step 2路径选择.

运用该算法求解多式联运起点到终点的最短路径，如果选择该路径，计算该路径的费用，进入Step 3；否则，将此粒子的适应度函数值设定为无穷小，重复Step 2.

Step 3可靠性检测.

根据Step2的路径方案，对速度根据样本的大小进行抽样，得到该路径下的目标期望值，期望值保持不变，进入Step 4.

Step 4路径更新.

选出所有路径中期望值最小的路径，进入Step 5.

Step 5终止条件.

经过p次循环后，适应度函数值不发生改变，运行停止，获取最小的目标函数期望值、成本、运输路径及方式；否则，转回Step 2.

2.3 基于优先权的粒子解码和编码设计

将网络中所有节点的权重赋值为实数，以扩大粒子的搜索范围.基于优先权的粒子群算法的解码设计：首先，设定网络起点，将其权重赋值为无穷小；其次，根据节点序号，依次在网络中选出权重最大的节点，组成解码路径；同时，为了提高粒子解码的成功率，确保以选节点不再被选中，将已选节点的权重赋值为无穷小，如图2所示.

将粒子的维度分为3段进行编码，第1段表示完整的路径；第2段为节点间的运输方式；第3段为货物运量，如图3所示，n为完整运输路径中节点的个数.

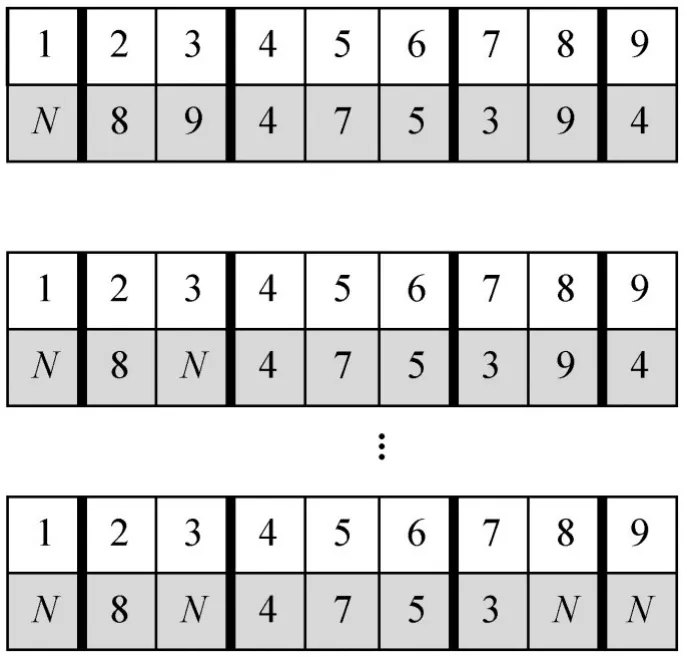
图2 基于优先权的粒子群解码图Fig.2 The decoding diagram of particle swarm optimization based on priority

图3 基于优先权的粒子群算法编码图Fig.3 The coding diagram of particle swarm optimization based on priority

3 模拟计算与结果分析

3.1 算 例

为验证模型与算法的有效性，随机生成11个节点和多条路径组成的有向多式联运网络，表2依次是公路、铁路、水路的运输距离.火车行驶速度约为60～80 km/h，将船舶和卡车的速度平均分为4段进行组合，构成表3所示的16种情景.

3.2 计算过程

由模型可知耗油量与成本成正比关系，耗油量的多少是计算成本的关键环节，为显示模型计算过程，本文从耗油量入手，探索速度与耗油量之间的关系，为后面章节的计算结果提供依据.由图4得出当货车的运行速度在60 km/h时货车的耗油量最小，由图5得出船舶耗油量随着速度的增加而增加.

表2 多式联运网络各节点间的运输距离Table 2 Transport distance between nodes of intermodal transport network

表3 速度情景组合Table 3 Velocity scenario combination

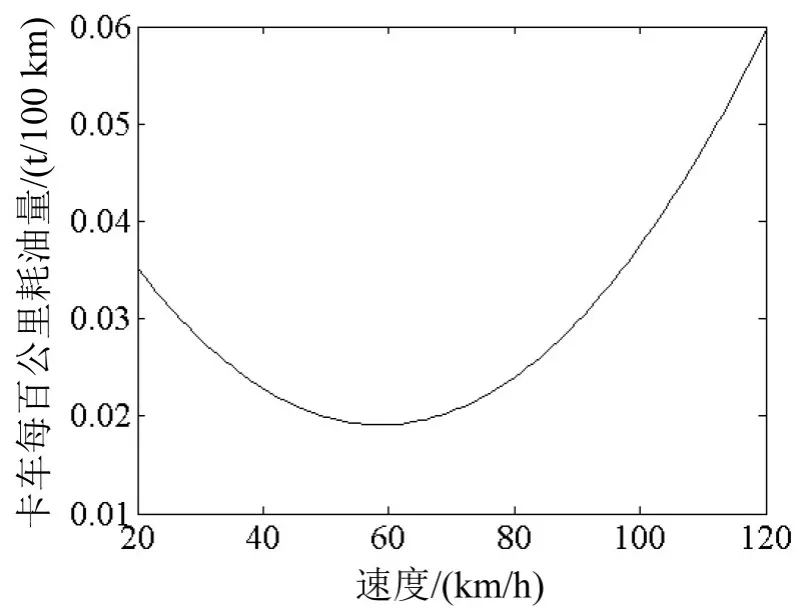
图4 卡车每百公里耗油量Fig.4 The fuel consumption per hundred kilometers of truck

3.3 样本规模分析

随机解的质量取决于样本的大小，本节探索了求解过程中样本大小对目标期望值的影响，得出图6中情景3-2的样本规模从100到800的可靠性和稳定性评估.y1、y2、y3、y4、y5代表的是当碳排放成本系数为0.0、0.2、0.5、0.8、1.0，运输成本系数为1.0、0.8、0.5、0.2、0.0的目标期望值.得出当样本规模为600时，目标函数的期望值趋向于稳定，具有可靠的目标函数解.

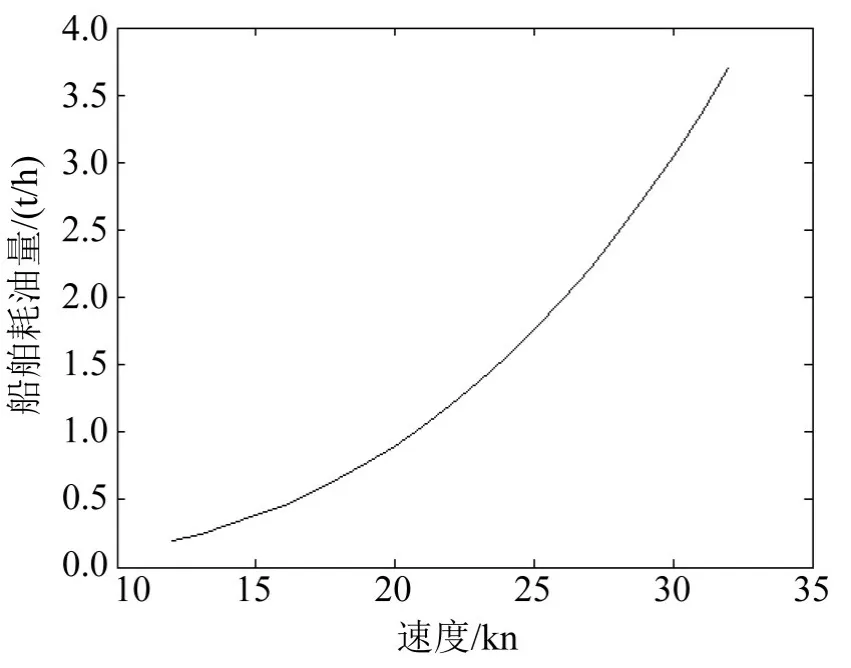
图5 船舶每小时耗油量Fig.5 The fuel consumption per hour of ship

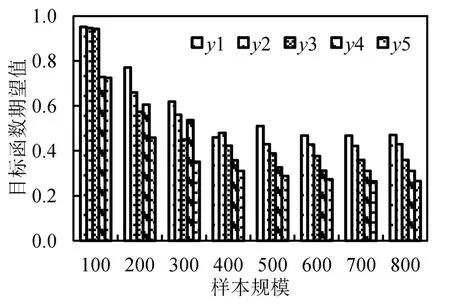
图6 目标函数迭代图Fig.6 Objective function iterative graph

3.4 情景分析

本文结合多式联运的实际运营情况，对多式联运的随机优化问题进行分析.碳排放权重系数为0.5时，速度服从正态分布和均匀分布，以及匀速时多式联运网络的运输路径与方式、成本取值和期望值的变化规律，如图7～图10和表4所示.

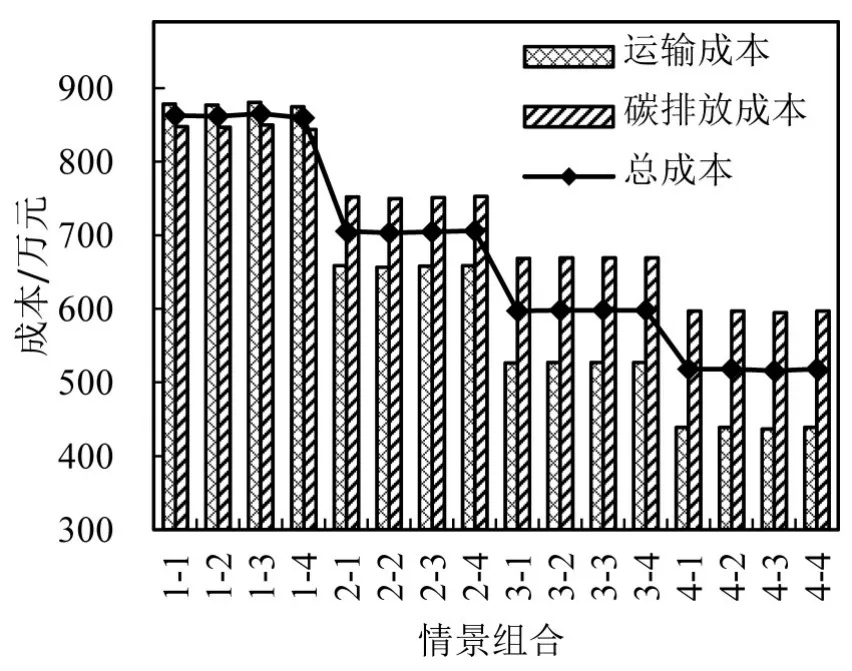
图7 匀速时不同情景的成本Fig.7 The cost of different situations at uniform speed

图8 正态分布时不同情景的成本Fig.8 The cost of different scenarios in normal distribution

图9 均匀分布时不同情景的成本Fig.9 The cost of different situations in uniform distribution

图10 目标函数期望值Fig.10 Objective function expected value

通过表4与图7～图9的情景1-1/2/3/4得出船舶降速，导致水上运输时间延长，使得货物运输转向运费较高但运输时间较短的公路或铁路运输，运输成本增加.由图5可知船舶降速耗油量会有所减小，但为了客户需求可适当降速，以维持市场占有量.结合实际情况，速度服从均匀分布时，情景2-2/3，3-2/3组合是成本较小和稳定性较高的理想选择，运输路径多选择2/3/6/9节点，运输方式多为节能减排的海铁联运，该结论与图4中卡车最低耗油量数据相符.

图8中速度服从均匀分布时期望值略低于速度服从正态分布的期望值，期望值越小网络的稳定性越强，运营过程中受到速度不确定性的影响因素较小，因此速度的变化范围越小对成本的控制越有利.

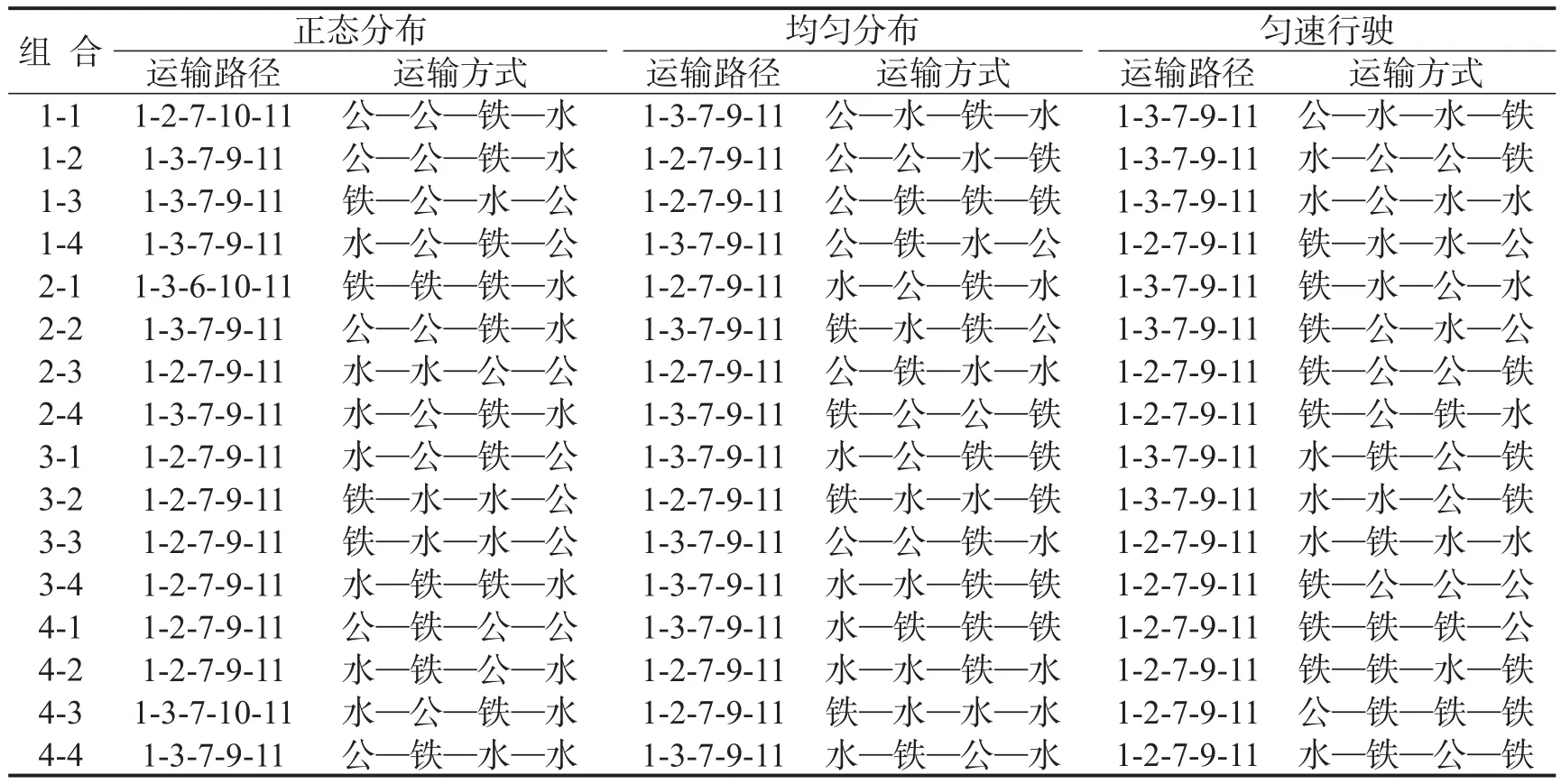
表4 运输路径与方式Table 4 The form of transport path and transport mode

3.5 碳排放权重系数分析

碳排放系数对成本会产生一定的影响，但影响程度未知.本节针对不同的碳排放系数，对3个作业成本进行分析.结果如图11～图13所示，其中Nc、Nt、Nz；Uc、Ut、Uz分别代表速度服从正态分布和均匀分布的碳排放成本、运输成本及总成本.

图11 碳排放权重系数为0.2时成本折线图Fig.11 The cost line diagram of carbon emission weight coefficient is 0.2

图11～图13，对于不同的速度分布，当碳排放成本权重系数增加时，有利于运输成本和碳排放成本的减小.具体情况如下，对于不同的权重系数情景2-2/3/4中，当速度服从正态分布时的碳排放成本减幅大于均匀分布时碳排放成本减幅，当系数增加到0.8，两碳排放成本持平.针对情景3-2/3/4，当碳排放权重系数增加时，速度服从均匀分布的运输成本的减幅大于正态分布时运输成本的减幅，系数为0.5，速度服从均匀分布的运输成本开始小于正态分布的运输成本.

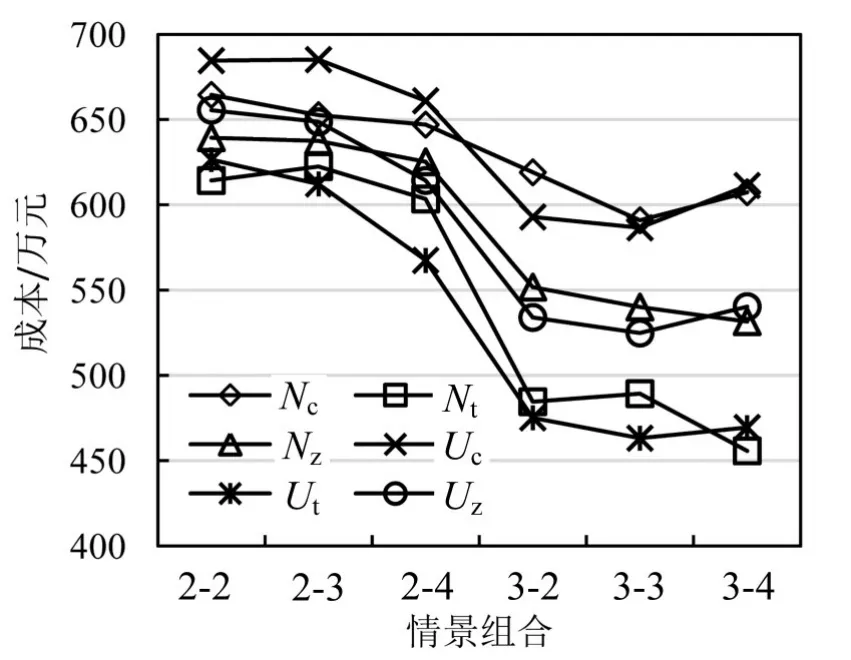
图12 碳排放权重系数为0.5时成本折线图Fig.12 The cost line diagram of carbon emission weight coefficient is 0.5

图13 碳排放权重系数为0.8时成本折线图Fig.13 The cost line diagram of carbon emission weight coefficient is 0.8

图14 算法的开拓性能和开掘性能Fig.14 Algorithm development performance and excavation performance

图14是权重系数均为0.5，样本规模为600，速度服从正态分布时情景1-2的目标函数的在线性能和离线性能曲线.在线性曲线为粒子群算法的最优适应度值与平均适应度值在迭代中的演变过程，在线性能反映出粒子群算法较好的开掘性，可以较快搜寻到最优解并保持稳定；离线性能图则说明粒子群算法保持较好的开拓性，在迭代一定次数后，粒子群的搜索范围不断缩小且集中于最优解的周围，也展示出良好的收敛效率与求解质量.

4 结论

本文分析了速度服从随机分布时多式联运网络中涉及到的各项成本和碳排放的影响因素，计算得出了不同情境下较为理想的运力配置方案.碳排放是影响多式联运网络优化的要素，也是发展绿色交通运输、节能减排的重点研究领域.政府可以根据碳排放成本的变化规律，制定出节能减排的有效措施，促进企业朝着绿色低碳方向发展.本文研究多式联运的路径优化时未考虑当需求不确定时路径中的资源配置问题.这是以后需要进行进一步研究的重点.