基于原模图的欧氏几何准循环LDPC码

刘原华, 何 华

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

低密度奇偶校验(low-density parity-check， LDPC)码是一种具有稀疏校验矩阵的线性分组码，能够利用低复杂度迭代译码算法达到接近香农限的纠错性能。LDPC码可分为随机LDPC码和结构化LDPC码。随机LDPC码围长较大，性能优异，但由于缺乏一定的结构特性，编码复杂度高，不利于硬件实现，且校验矩阵的存储复杂度也较高。结构化LDPC码具有循环或准循环的结构，可实现线性复杂度的编译码，中短码长时性能可与随机码相比拟，正逐步进入各种通信领域，在中国数字电视地面广播传输标准、欧洲第二代数字电视地面广播标准、无线局域网IEEE 802.16n中均已采纳准循环LDPC(quasi-cyclic LDPC，QC-LDPC)码作纠错编码方式。

绝大多数欧氏几何LDPC码都是结构化的循环码或准循环码，可以通过移位寄存器实现线性复杂度编码,同时可利用多种译码算法实现复杂度、速度以及纠错性能之间的良好折衷。利用欧氏几何的结构特性,可构造出不包含4环的性能优异的LDPC码[1-7]。基于欧氏几何的QC-LDPC码[6]虽然不包含4环，但在校验矩阵的行重和列重给定的情况下，其译码门限就确定了，无法进一步有效改善QC-LDPC码的纠错性能。

原模图QC-LDPC码可以由一个很小的原模图通过复制和循环矩阵扩展得到，其纠错性能由原模图、复制次数以及循环矩阵的移位数共同决定。原模图QC-LDPC码与一般的QC-LDPC码的不同之处在于，其基矩阵中的元素不仅仅局限于0和1，可以是任意小于其复制次数的非负整数，即原模图具有允许多边存在的特点，有利于降低码的译码门限，进一步优化QC-LDPC码的性能。基于Sidon序列的QC-LDPC码[8]属于一种原模图QC-LDPC码，其基矩阵中的元素均为2。对于给定的原模图，为避免短环的出现，在设计循环矩阵的移位次数时需考虑原模图中的环分布情况[9-12]。例如,在利用PEG算法构造原模图QC-LDPC码时，通常先要基于PEG算法构造原模图，再借助附加的环检测算法来设计循环矩阵的移位次数[13-15]。这种方法可有效地构造短码长的性能优异码，但当码长增加时，该方法的复杂度将很高。

为简化构造算法的复杂度，同时改善欧氏几何QC-LDPC码的纠错性能，本文拟给出一种基于原模图的欧氏几何QC-LDPC码构造方法。利用欧氏几何的结构特性设计循环矩阵的移位次数，有效避免短环的出现，简化实现复杂度；同时将原模图多边的特点引入欧氏几何码的基矩阵，降低译码门限，进一步优化其纠错性能。

1 原模图QC-LDPC码

原模图是节点相对较少的Tanner图，记为

Gp=(V，C，E)。

其中V是变量节点集和，C是校验节点集和，E是边集和。原模图对应的基矩阵为

B=(bij)m×n。

其中m为校验节点的个数，n为变量节点的个数，bij为第i个校验节点和第j个变量节点之间连接边的条数，当bij>1时，原模图中有并行边的存在。对原模图进行T次复制，然后把T条相同类型的变量节点和校验节点之间的边置换，可以扩展成不同大小的图，这种图称为导出图G，对应的LDPC码称为原模图LDPC码。若边置换为循环置换，则对应的LDPC码为原模图QC-LDPC码。

原模图QC-LDPC码可由其基矩阵经循环矩阵扩展得到：将基矩阵中的非零元素，用bij个不重叠的循环置换矩阵的和替换，零元素用全零矩阵替换，即可得到原模图QC-LDPC码的校验矩阵H，该操作称为循环矩阵扩展。

2 原模图欧氏几何QC-LDPC码

LDPC码的性能可由译码门限值来衡量，门限值是LDPC码成功译码所能容忍的最小信噪比，当信道的信噪比高于门限值时，码集中的几乎任何一种码的误比特率都将随着迭代次数或码长的增加而趋于零，否则码集中的码的误比特率将始终大于某个常数。因此，这个门限值是评价LDPC码性能的重要参数。外信息转移(extrinsic information transfer，EXIT)图技术是分析LDPC码迭代译码性能的有效方法之一，可根据LDPC码的度分布，计算其译码门限。具有相同度分布的QC-LDPC码可以具有不同的基矩阵，从而具有不同的译码收敛性能，而传统的EXIT图无法区分这些QC-LDPC码译码性能的不同，故需引入基于原模图的EXIT(protograph EXIT，PEXIT)图技术[16]，用以分析相同度分布不同基矩阵的原模图QC-LDPC码的译码门限。

基于原模图构造欧氏几何QC-LDPC码，需先构造具有低译码门限的多边原模图的基矩阵，再利用欧氏几何的结构特性设计循环矩阵的移位次数，并通过循环矩阵扩展获得不包含4环的欧氏几何原模图QC-LDPC码。

2.1 欧氏几何

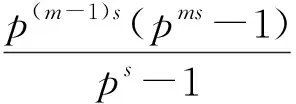
令伽罗华域FG(pms)为域FG(ps)的扩域，可以看作是FG(ps)上的所有m维向量构成的向量空间，FG(pms)上的任意元素可表示成为FG(ps)上的m维向量，域FG(pms)上的pms个元素与欧氏几何GE(m,ps)中的pms个点一一对应，因此,伽罗华域FG(pms)等价于GE(m,ps)[6]。FG(pms)中的每个元素可由其本原元α的幂次表示，欧氏几何中的每个点也可由α的幂次来表示，其中α∞表示原点。

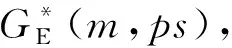
将有限域FG(pms)中的一个本原元记为α，令

ai=αi-1(i=1,2,…,n)

v(ai)=(v1,v2,…,vn)，

vL=(v1,v2,…,vps)，

该向量包含ps个子向量，每个子向量为n维二进制向量，其中第i个子向量vi是直线L上第i个点的关联向量。

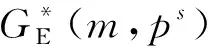
任一循环类中任一直线均可作为此循环类的代表元，将代表元的关联向量进行分段循环移位n次即可得到该循环类中的其他直线的关联向量。

2.2 改进欧氏几何码设计

对于第i个循环类(i=1,2,…,K)，将该类中n条直线的关联向量作为列，可构造出nps×n阶矩阵Hi。由直线的循环特性可知，Hi可设计成一个由n×n的循环置换矩阵组成的ps×1矩阵阵列，Hi的每行包含1个非零元素1，每列包含ps个非零元素1，其余元素皆为0，即Hi的行重为1，列重为ps。将这K个矩阵H1，H2,…，HK作为子矩阵构造矩阵

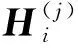
选择H的任意γ×ρ子阵列，即可得到(γ，ρ)规则欧氏几何QC-LDPC码[6]，其中γ和ρ为码校验矩阵的行重和列重。该码的基矩阵为一个γ行ρ列全1矩阵，其译码门限可由PEXIT算法计算得到。因此，无论如何选择H的子阵列，只要参数γ和ρ确定了，其译码门限就固定不变了，无法进一步有效改善QC-LDPC码的纠错性能。为解决这一问题，考虑利用原模图码的特点，将大于1的元素引入到基矩阵中，从而优化QC-LDPC码的纠错性能。

原模图QC-LDPC码中存在不可避免短环的问题[9]，若QC-LDPC码的基矩阵包含元素3，则无论如何设计循环矩阵的维数(即复制次数)和循环矩阵的移位次数，必定存在长度为6的不可避免短环；若基矩阵的某行或某列包含两个2，则必定存在长度为8的不可避免短环。基于以上结论，在设计基矩阵时，除了元素0和1，只引入元素2，不考虑元素3，且每行每列最多包含一个2。由于LDPC码校验矩阵的行重大于列重，即基矩阵的列数ρ大于行数γ，不失一般性，将元素2设计在基矩阵的前γ列，且处在基矩阵左边γ行γ列子矩阵的对角线位置。为保证LDPC码的列重不变，基矩阵的前γ列每列需设置一个元素0，为保证LDPC码的行重不变，这γ个0需处在不同行且不同列。

例如，当γ=4，ρ=8时，基矩阵可设计为

(1)

其译码门限可由PEXIT算法计算得到，与4行8列的全1基矩阵相比，式(1)的译码门限获得了0.247 5的改进，其对应原模图QC-LDPC码的性能可得到有效提高。

利用欧氏几何的结构特性可设计循环矩阵的移位次数，再通过循环矩阵扩展，即可获得不包含4环的欧氏几何原模图QC-LDPC码。

假设原欧氏几何QC-LDPC码的校验矩阵是由n×n的循环置换矩阵组成的γ×ρ的矩阵阵列，具有形式

(2)

其中Iaij为n×n的循环置换矩阵，可由单位阵I每行向右循环移位aij位得到，而aij为该循环置换矩阵的循环移位次数，其值由欧氏几何中直线的关联向量确定。

矩阵(2)的基矩阵为一个γ行ρ列全1矩阵，为获得形如式(1)的基矩阵，将矩阵H前γ列阵列的每列选择一个子矩阵移入到左半边阵列的对角线对应的子矩阵Iaii(1≤i≤γ)中，基矩阵中的元素2对应的循环子矩阵为2个不重叠的循环置换矩阵的叠加。以式(1)的基矩阵为例，改进后的校验矩阵

H′=[h1,h2,h3,h4,h5,h6,h7,h8],

(3)

h1=[Ia11+Ia21,0,Ia31,Ia41]T,
h2=[0,Ia22+Ia12,Ia32,Ia42]T,
h3=[Ia13,Ia23,Ia33+Ia43,0]T,
h4=[Ia14,Ia24,0,Ia44+Ia34]T,
h5=[Ia15,Ia25,Ia35,Ia45]T,
h6=[Ia16,Ia26,Ia36,Ia46]T,
h7=[Ia17,Ia27,Ia37,Ia47]T,
h8=[Ia18,Ia28,Ia38,Ia48]T,。

其中0为零矩阵，其零空间即为所设计的原模图QC-LDPC码。

2.3 码结构分析

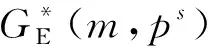
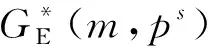
3 仿真结果

对改进方法构造的原模图QC-LDPC码和已有欧氏几何码[6]的译码门限进行比较，同时采用二进制相移键控调制下的加性高斯白噪声信道，仿真比较改进方法和已有方法构造的QC-LDPC码在置信传播迭代译码算法下的误比特率(bit error rate，BER)和误帧率(frame error rate，FER)，译码的最大迭代次数设置为100次。

两种方法构造的三组(6,9)，(4,8)和(4,10)规则QC-LDPC码的译码门限如表1所示。由其可见，与原欧氏几何码相比，改进方法构造的QC-LDPC码译码门限更低，三组码的门限改进值均大于0.2。

表1 译码门限对比

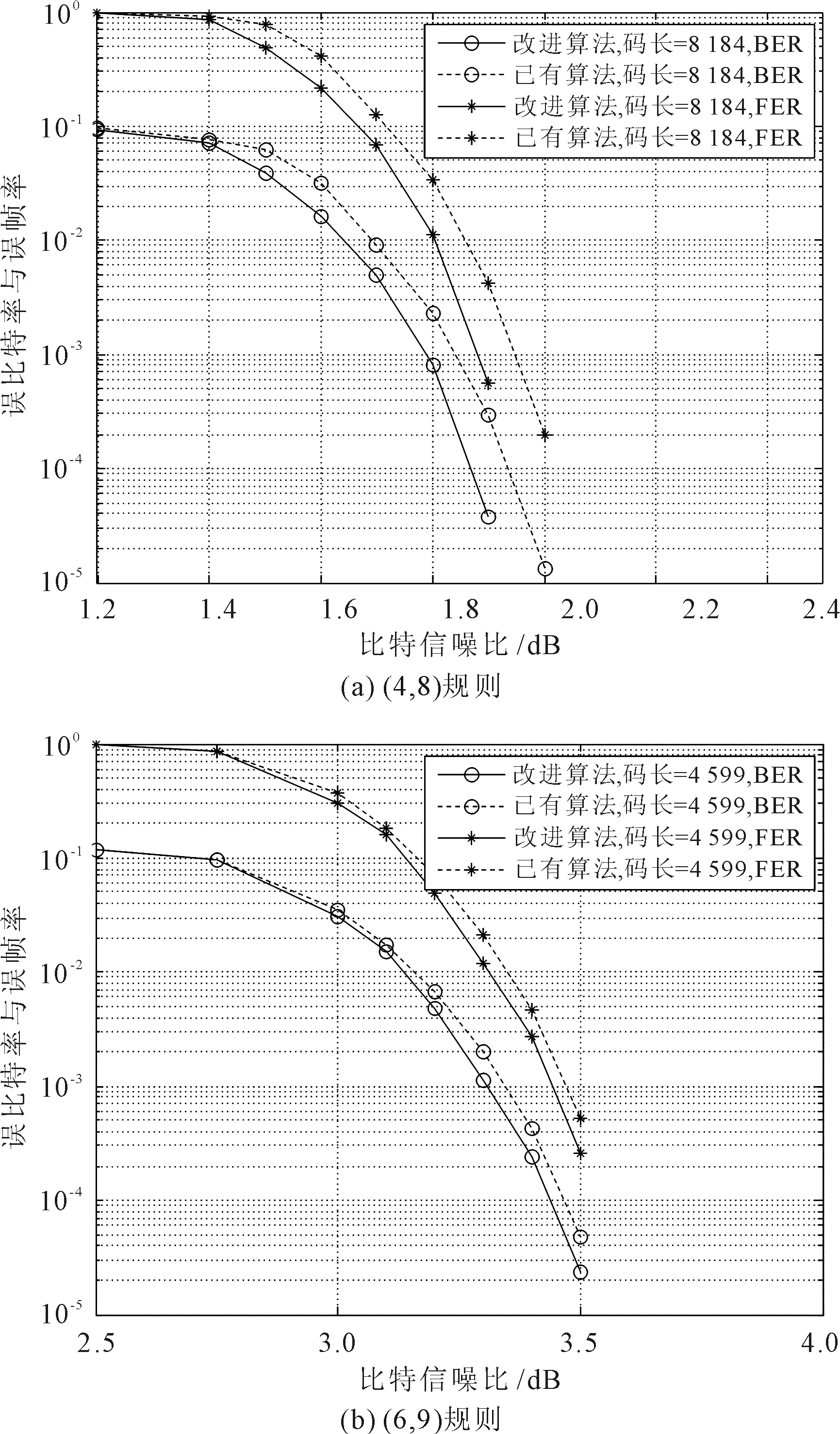
图1 两种方法构造QC-LDPC码的纠错性能

4 结论

为降低码的译码门限,首先构造了基于多边的原模图的基矩阵，然后利用欧氏几何的结构特性设计基矩阵对应的循环矩阵的移位次数，获得了不包含4环的欧氏几何原模图QC-LDPC码。仿真结果表明，与已有欧氏几何码相比，改进方法构造的QC-LDPC码通过降低译码门限获得了更优的纠错性能。同时，所构造的码具有准循环的结构，具有编译码实现简单的特点。