一种基于模糊逼近的双容水箱鲁棒控制器设计

王文庆, 马一鸣

(西安邮电大学 自动化学院，陕西 西安 710121)

液位控制是工业生产中的一类常见问题，在饮料和食品加工、溶液过滤、化工生产等多种行业的生产加工过程中都需要对液位进行适当的控制[1]。大部分液位控制系统可以抽象为双容水箱液位控制模型[2-3]。双容水箱作为一种典型的非线性时滞被控对象，研究其建模和控制具有重要的意义。

可以利用传递函数系统建模[4-6]来研究双容水箱的液位控制。作为一种系统外部描述，传递函数对于单输入-单输出线性定常系统的分析和综合比较有效，但其只能反映系统外部变量间的因果关系，难以揭示系统内部的结构特性，也难以有效处理多输入-多输出系统[7]。

状态空间的描述方法不但可以反映系统的输入-输出外部特性，而且能够揭示系统的内部结构特性，其既适用于单输入-单输出系统又适用于多输入-多输出系统[7]。工程应用中，系统的结构机理很难描述，非线性、不确定因素很难用精确的数学模型衡量[8]。目前关于非线性、不确定系统的研究主要运用范数有界不确定性假设以及匹配条件假设，多集中于具有时滞的非线性、不确定系统稳定性方向，这一点并不切合实际[8]。例如，文[9]以范数有界性定理为前提，研究满足鲁棒稳定性条件的不确定干扰；文[10]研究的鲁棒控制问题是一类带非线性扰动的范数有界,时变参数不确定系统；文[11]以系统状态反馈控制率为研究对象，其不确定性参数具有时变未知,但范数有界的特点；文[12]采用了构造Lyapunov-Krasovskii泛函时间导数上界的方法研究时滞相关稳定性。以上研究均要求受到不确定干扰的研究对象满足匹配条件，而在工业实际生产中，满足范数有界不确定性假设以及匹配条件假设的不确定干扰无法涵盖所有的不确定干扰情况，这些稳定控制方法依旧具有较大的局限性，无法有效地控制不满足条件的非线性及不确定干扰，可控范围相对较小。

基于以上分析，本文拟采用状态方程的方法对水箱系统进行研究分析，着重分析水箱系统中的非线性干扰因素，并进一步研究不满足匹配条件的不确定干扰的双容水箱系统的鲁棒控制，依据文[8]的非线性鲁棒控制理论，结合模糊系统，设计模糊非线性逼近器，并仿真验证该控制理论的实际可行性及控制效果。

1 双容水箱系统建模

工业水箱系统可抽象为一个双容水箱液位系统，由上、下两个水箱组成，如图1所示。

图1 双容水箱模型

图1中，上水箱W1的长、宽、高分别为l1、w1、h1，横截面积为S1；下水箱W2的长、宽、高分别l2、w2、h2，横截面积为S2。上水箱W1上端有一入水阀门T0，上、下水箱间有控水阀门T1相连，下水箱W2底部有一出水阀门T2，阀门T0、T1、T2的管径分别为d0、d1、d2，其阻力系数分别为R0、R1、R2。

根据物料平衡原则[4]，分别对水箱W1、W2建立平衡方程式

(1)

(2)

其中，D0为上水箱W1的入水量；D1为上水箱W1的出水量，即下水箱W2的入水量；D2为下水箱W2的出水量；H1为上水箱W1的液位高度；H2为下水箱W2的液位高度；t为时间变量。根据经验公式[13]

整理得

(3)

其中

C1=S1R1,C2=S2R2。

设计双容水箱液位系统为单输入-单输出系统，系统输入为上水箱W1的入水流量D0，系统输出为下水箱W2的液位高度H2，令

则系统状态方程为

(4a)

(4b)

式(4)是抽象双容水箱液位系统的状态方程，是一个相对理想的数学模型，是无干扰、无时滞情况下的数学抽象。记

式(4a)又可写为

x′=Ax+Bu。

(5)

实际工业生产过程存在非线性因素。双容水箱液位系统中，不确定性因素主要包括2个方面：一是系统本身的不确定性，例如水箱工作环境的变化、控水阀门参数的不确定性、降阶和非线性系统的线性化等；二是外部干扰的不确定性，例如被控过程中的各种干扰信号。因此，式(5)所表示的理想系统与实际情况相比误差较大。

设考虑各种不确定性及输入干扰后式(5)的一般形式为

x′=Ax+Δf(x,t)+B(u+Δg(x,t))。

(6)

其中，Δf(x,t)是系统的结构不确定性或干扰，主要来源于水箱、阀门参数、建模线性化假设等；Δg(x,t)是系统的输入通道上的不确定性或干扰，主要来源于环境干扰等。该系统的状态反馈闭环结构，如图2所示。

图2 系统(6)状态反馈的闭环结构

图2中，C表示需要合成的非线性鲁棒控制器。显然，式(6)的系统不再是线性的，常规的线性反馈控制器无法对其镇定。下面将针对式(6)系统设计一个非线性控制器。

2 控制器设计

为了设计非线性控制器，对式(6)系统的不确定性作如下假设

‖Δf(x,t)‖≤ζ(x),x∈U;‖Δg(x,t)‖≤η(x),x∈U。

(7)

其中，ζ(x)、η(x)是未知的非负连续函数，‖·‖表示欧式范数。

由线性系统理论可知，式(6)所对应的式(5)为线性系统，即存在一个线性反馈u=Kx,使对任意给定的正定对称矩阵Q，Lyapunov方程

(A+BK)TP+P(A+BK)=-Q

(8)

存在唯一正定矩阵解P。

考虑(6)所表示的系统，设计如下非线性鲁棒控制器

u=ua+ub+uc。

(9)

其中

(10a)

(10b)

其中，α、β为可调正常数，满足

(11)

其中，λmax(P)表示矩阵P的最大特征值，λmin(Q)表示矩阵Q的最小特征值。α、β应根据系统(6)的状态、自适应律、收敛速度及范围来选取。若取

则式(11)被满足。

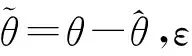
其中，取正定函数

是常数，取λ=min{λ0,α,β}。

3 模糊系统设计

本部分设计相关的非线性逼近器。根据模糊系统的万能逼近性质，构造非线性逼近器，作用于复杂系统(6)中的不确定干扰。选用由模糊规则库、模糊推理机、模糊产生器和模糊消除器4部分组成的模糊系统，如图3所示。

式中直接电能Edirect的计算方式如式(1)～式(8)所示，间接能耗Eindirect的计算方式如式(9)～式(15)所示。

图3 模糊系统结构图

以单点模糊化、乘积推理、中心解模糊和具有如下的模糊规则的模糊系统为例

(12)

(13)

为常数。若令

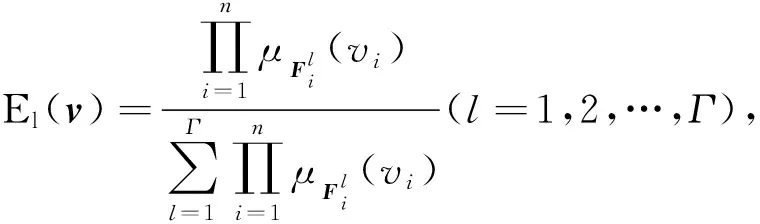
则式(13)可以表示为

z=θTE(v)。

(14)

即为所寻找的非线性逼近器。该逼近器可以以任意精度逼近有界闭集上的未知连续函数[16]。

4 仿真结果及分析

4.1 水箱系统的初始参数与Simulink模型

使用MATLAB 8.6软件包仿真。基于模糊非线性逼近的鲁棒控制Simulink模型，如图4所示。

图4 双容水箱鲁棒控制Simulink仿真模型

模糊逼近器模块为双输入-单输出系统，输入Ⅰ为水箱W2液位高度，输入Ⅱ为水箱W2液位高度变化率；输出结果为水箱系统总进水量D0。

选取水箱W1尺寸为长3 m、宽2 m、高2.5 m，水箱W2尺寸为长3 m、宽2 m、高2.5 m；阀门T0、T1、T2的管径分别取为d0、d1、d2均为0.02 m，经查表得其阻力系数分别为

R0=0.15,R1=0.15,R2=0.15。

通过分析水箱实验模型，水箱W2液位高度的区间选取为[0,2.5]，水箱W2液位高度变化率的区间选取为[-17,5]，水箱系统总进水量D2的区间选取为[0,18]。系统的设计目标为控制水箱W2液位高度并使其保持在区间(0,2.5)内。

将输入Ⅰ的语言值用模糊集合“水位低(h1)”、“水位较低(h2)”、“水位适中偏低(h3)”、“水位适中(h4)”、“水位适中偏高(h5)”、“水位较高(h6)”、“水位高(h7)”表示；将输入Ⅱ的语言值用模糊集合“负小(r1)”、“负较小(r2)”、“负中(r3)”、“负(r4)”、“零(r5)”、“正(r6)”、“正大(r7)”表示；将输出的语言值用模糊集合“关(q1)”、“半关(q2)”、“小开(q3)”、“中开(q4)”、“开(q5)”、“大开(q6)”、“全开(q7)”表示。即

输入Ⅰ 水箱W2液位高度

{h1,h2,h3,h4,h5,h6,h7}。

输入Ⅱ 水箱W2液位高度变化率

{r1,r2,r3,r4,r5,r6,r7}。

输出 水箱系统总进水量D0

{q1,q2,q3,q4,q5,q6,q7}。

建立的模糊规则，如表1所示。

表1 模糊规则表

经反复试验，选取模糊输入Ⅰ、Ⅱ及输出的隶属函数，如图5所示。

(a) 输入Ⅰ

(b) 输入Ⅱ

(c) 输出

4.2 模糊逼近控制器控制效果验证

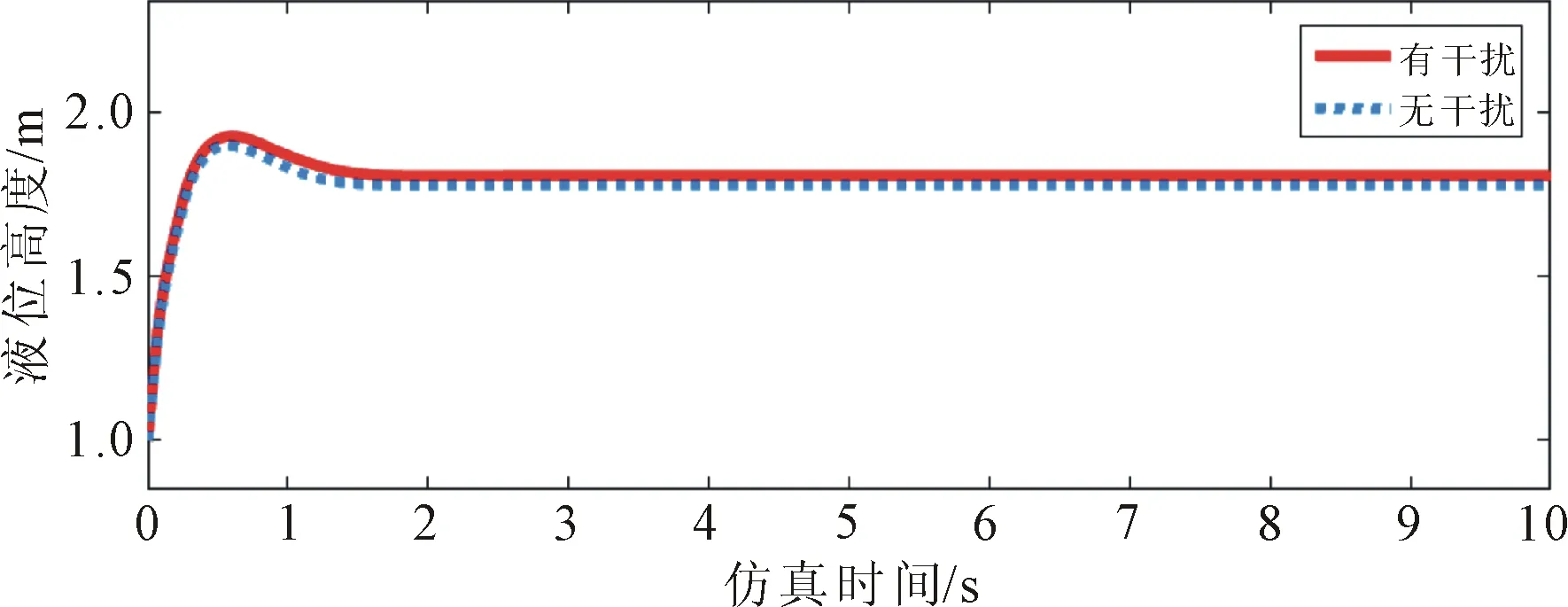
仿真初始值选取x1=1 m，x2=1 m/s；首先假设干扰为零。模糊逼近器仿真效果，如图6所示。

图6中，虚线为无干扰时控制器作用下的W2液位高度变化曲线，即水箱系统在理想环境中的工作状态。可以看出，系统在极短的时间内达到了平衡状态，上升沿和峰值出现的时间都很短，调节很快，且超调量极小，控制性能良好。

首先取干扰项

仿真曲线如图6(a)所示。可以看出，加上干扰对控制效果无显著影响，即说明控制器对该非线性干扰的控制有效。

进一步取干扰项分别为

Δf2=x2sinx1+0.1,
Δg2=x2cos(x2x1),
Δf3=x2sinx1+x2cos(x1x2),
Δg3=x2cos(x2x1)+x2,
Δf4=x2ex2sinx1+x2cos(x1x2),
Δg4=x2cos(x2x1)+x2sinx1,

仿真曲线如图6(b)、图6(c)、图6(d)所示。从图中可以看出，虽然干扰项的复杂性不断增加，除超调量有所增加外，其它各项性能指标依然良好，表明所设计控制器的抗干扰性能良好。

(a) 当干扰为Δf1、Δg1时的水箱液位高度

(b) 当干扰为Δf2、Δg2时的水箱液位高度

(c) 当干扰为Δf3、Δg3时的水箱液位高度

(d) 当干扰为Δf4、Δg4时的水箱液位高度

4.3 与基于传递函数的控制器仿真对比

为进一步验证控制器的鲁棒性，将模糊逼近器与文[6]中的基于传递函数的控制器进行仿真对比，随机选取3组不同的初始值进行仿真，第一组初值为

x1=1,x2=-1；

第二组初值为

x1=2,x2=1.1；

第三组初值为

x1=0.5,x2=-5。

每组初值均在无干扰和有干扰情况下仿真，干扰项统一选为

Δf4=x2ex2sinx1+x2cos(x1x2),
Δg4=x2cos(x2x1)+x2sinx1。

仿真结果，如图7～图9所示。

(a) 无干扰

(b) 有干扰

(a) 无干扰

(b) 有干扰

(a) 无干扰

(b) 有干扰

图7～图9中，虚线为基于传递函数的控制器作用下的曲线，实线为本文设计控制器作用下的曲线。每组图中，图(a)为无干扰的情况，图(b)为加入干扰时的情况。

从图7(a)可以看出，基于传递函数的控制器的仿真结果图有一个明显向下的峰值，超调量明显大于模糊逼近器的仿真结果，且基于传递函数的控制器的波形在仿真时间为15 s时才趋近平衡，调节时间远远大于模糊逼近器控制下的仿真结果。在图7(b)中，干扰对模糊逼近器控制下的系统仿真结果没有明显的影响，各项性能指标与无干扰时没有差别，而基于传递函数的控制器控制下的系统仿真结果的超调量有所增加。

从图8(a)、图8(b)可以看出，在该组初始值情况下，模糊逼近器与基于传递函数的控制器作用下的仿真结果超调量基本相同，但基于传递函数的控制器作用下的仿真结果的调节时间依然大于模糊逼近器控制下的系统仿真结果。两种控制器对于干扰的控制作用均较为稳定。

图9(a)显示，在模糊逼近器控制下的系统仿真结果的超调量极小，调节时间很短，而基于传递函数的控制器作用下的仿真结果超调量较大，调节时间远大于模糊逼近器的仿真结果，且下水箱液位高度在短时间内为负数值，从实际物理意义分析，已经超出了区间范围，也可以说基于传递函数的控制器未对水箱液位系统产生有效的控制。图9(b)中模糊逼近器控制结果有效且控制性能良好，而基于传递函数的控制器仿真结果存在波动，且仿真波形超出区间范围。所设计的模糊逼近器的控制范围较基于传递函数的控制器大，对系统初值的选取不敏感，鲁棒性强。

6 结语

针对双容水箱的液位控制问题，以物料平衡原理和状态方程的方法，建立了区别于基于传递函数的控制方法的液位控制系统动态模型；根据模糊系统的万能逼近性质及鲁棒控制原理，设计了基于模糊非线性逼近的鲁棒控制器。利用MATLAB软件包对该控制器进行了仿真，并利用双容水箱系统验证该控制器的控制效果。通过选取多组水箱系统初始值验证了控制器的稳定性，证明该控制器对于系统初值选取不敏感；通过不同复杂度的不确定项，证明了随着不确定干扰复杂度的增加，除超调量有所增大外，其他控制性能没有明显变化，控制效果较好。将本文所设计的非线性鲁棒控制器与基于传递函数的控制器进行仿真对比，结果发现，当不确定干扰复杂度增加、初值选取变化较大时，传递函数控制器已无法有效控制系统稳定，而所设计的鲁棒控制器依然控制有效且性能稳定，较传递函数控制器，该控制器调节时间更短，超调量更小，对初值选取不敏感。