两阶段判别嵌入式聚类

支晓斌, 李亚兰

(1.西安邮电大学 理学院， 陕西 西安 710121； 2.西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

聚类是按照一定的要求和规律对事物进行区分和分类的非监督模式识别过程，被广泛应用于众多领域，包括图像处理、信息检索、数据挖掘等[1]。其目的是将相似的样本分配到同一类，不相似的样本分配到不同类，并揭示数据有意义的结构。在实际应用过程中，通常遇到高维数据集，数据的高维度性不仅增加了算法的计算时间和内存需求，而且由于噪声效应和空间维度的欠采样，会对聚类性能产生不利影响，这一现象被称为“维数诅咒”[2]。因此，高维数据聚类成为聚类分析研究的难点和热点问题之一，而实际应用过程中普遍存在的高维数据使得对高维数据的聚类分析具有重要意义。

对于高维数据的聚类问题，现存在众多具有针对性的聚类方法[3-10]。无监督的判别聚类(discriminative clustering, DC)算法[3]将聚类和线性判别分析(linear discriminant analysis, LDA)[4]结合起来，实现了在降维过程中对数据的聚类。由于聚类是在LDA降维后的子空间中完成的，故DC算法常常可以产生比K-均值(K-means, KM)算法[5]更优的聚类效果。从“核”方法的角度考虑，DC算法可等价于判别K-均值聚类(discriminative K-means, DKM)算法[6]，但存在散度矩阵奇异性问题。为避免DC算法中LDA的小样本问题[7]和克服散度矩阵奇异性问题，判别嵌入式聚类(discriminative embedded clustering, DEC)算法[8]将子空间学习和聚类统一起来，用基于子空间学习的最大间距准则(maximum margin criterion, MMC)[9]降维，以代替DC算法中的LDA降维，来得到最佳的判别向量。但是，这些算法都存在对高维数据计算复杂度高，聚类速度慢的问题。高效判别嵌入式聚类(efficient discriminative embedded clustering, EDEC)算法[10]利用QR[11]分解，并依据MMC对数据进行两次降维处理，可降低DEC算法的复杂度，但对数据的适应性较差。

为改善DEC算法的运行效率和EDEC算法对数据的适应性问题，本文给出两阶段判别嵌入式聚类(two-stage discriminative embedded clustering, TSDEC)算法。在EDEC算法的基础上引入正则化因子λ，得到EDEC算法的一种广义形式。当λ→∞时，TSDEC算法将退化为EDEC算法，而当λ取其它值时，则得到不同于EDEC的新算法，从而提高了EDEC算法对数据的适应性。此外，TSDEC与EDEC算法复杂度相当，主要时间计算复杂度都是O(nmc)(n代表数据样本的个数，m代表数据维数，c代表类数)，故适合处理比较大的高维数据。

1 DEC算法

为了使得DC 算法能够有效地对高维数据聚类，并且克服散度矩阵奇异性问题，DEC算法将几个经典降维方法统一到同一框架下，对数据聚类的同时实现降维，提高了DC算法的聚类效率。平衡参数η取不同值时，DEC算法可将已有的几个经典降维方法视为特殊情况。例如，当η→0时，DEC算法等价于通过主成分分析(principal component analysis, PCA)[12]先对样本降维，再对降维后数据用KM算法聚类；当η=1时，DEC算法等价于通过正交质心法(orthogonal centroid method, OCM)[13]先对样本降维，再对降维后数据用KM算法聚类；当η=2时，DEC算法等价于通过MMC先对样本降维，再对降维后数据用KM算法聚类；当η→∞时，DEC算法等价于通过正交最小二乘判别分析(orthogonal least squares discriminant analysis, OLSDA)[14]先对样本降维，再对降维后数据用KM算法聚类。

X=(x1,x2, …,xn)。

聚类的目标是将所有数据样本分成c类，设第j类为Xj，其中含有nj个数据样本(j=1,2,…,c)，以这些数据样本为列向量可构成m×nj的数据矩阵Xj。

DEC算法可以描述为优化问题

maxJDEC(W,H)=
tr {WT[Sb+(1-η)Sw]W},
s.t.WTW=I。

其中，η为平衡参数，W为样本由高维空间映射到低维空间的待求变换矩阵，矩阵H=(hij)n×c为待求隶属度矩阵，若数据样本xi属于第j类，则hij=1；否则，hij=0。类内散度矩阵Sw和类间散度矩阵Sb分别定义为

矩阵Hw和Hb分别定义为

Hw=[X1-v1e1,…,Xc-vcec],

(1)

(2)

其中，ej=(1,2,…,1)∈nj为行向量。

以m′代表嵌入子空间中数据的维数，T代表算法运行的迭代次数，那么，DEC算法的时间计算复杂度为O[(nm2+ncm′)T]。

2 TSDEC算法

TSDEC算法首先用奇异值分解方法代替EDEC算法中的QR分解对正则化的类间散度矩阵做预处理，对数据矩阵进行初次降维；然后，在低维空间利用DEC算法中的经典降维方法对数据进行二次降维；最后，对降维两次的数据进行聚类。初次降维后数据的维数可以达到c维，故可使第二次降维过程变得更加高效，提升算法对高维数据的聚类效率。另外，引入正则化过程，得到EDEC算法的一种广义形式，以提高EDEC算法对数据的适应性。

TSDEC算法详细步骤如下。

步骤1对原始数据集执行规范化和中心化过程，并初始化类标签矩阵H。

步骤2根据(2)式构造矩阵Hb。

步骤3对矩阵Hb进行奇异值分解,得

Hb=UΣVT,

其中，U∈m×m和V∈c×c为正交矩阵，Σ∈m×c为对角阵。

步骤4Σ的前c行c列构成方阵Σ1，以Ic代表c阶单位矩阵，将奇异值矩阵正则化为

再令

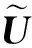
步骤5令

W=(w1,w2,…,wc)。

步骤7利用求得的特征子空间，计算最优变换矩阵G=QW。

步骤8利用y=GTx对数据进行投影变换，在降维后的投影空间中对数据执行KM聚类算法，更新隶属度矩阵H。如果满足‖H-H0‖<ε，则停止计算；否则，令H0=H，转回步骤3。ε为停止阈值。

TSDEC算法将DEC算法的主要计算复杂度由O(nm2)降低为O(nmc)，通常对于高维数据集有m≫c，因此，TSDEC算法在运行速率上与EDEC算法相当，而比DEC算法更高效。

TSDEC算法在EDEC算法的基础上增加了步骤4中的奇异值矩阵正则化过程，即令

3 实验结果及分析

将TSDEC算法与KM算法、DEC算法和EDEC算法在不同正则化参数下对6个数据集进行对比性实验。

3.1 实验设置

实验选取6个数据集，包括3个UCI数据集[15]Wine、Letter(abc)、Satimage，一个文本数据集[16]Doc，一个手写体数据集[17]MNIST和一个基因表达数据集[18]Global Cancer Map(GCM)。数据特性如表1所示。

表1 6个数据集的相关特性

实验在Intel Core i5 2.8 GHz CPU，4 GB内存Window 10环境下的电脑上进行运算。为了防止算法陷入局部最优，算法运行10次后取平均值。最大运行迭代次数设置为100，停止阈值ε设为10-5。

3.2 准确度测试

针对6个数据集，平衡参数η依次取值为2、1、1、∞、2、2，正则化参数λ的取值集合为{10-6，10-5，10-4，10-3，10-2，10-1，100，101，102，103，104，105，106}。4种算法在各数据集上的聚类性能随正则化参数的变化趋势如图1所示。其中，DEC算法在GCM数据集上运行内存溢出，无法获得聚类准确度，而KM算法、DEC算法和EDEC算法的聚类准确度各是一条不随正则化参数λ变化的直线。

由图1所示聚类结果可知，对于大多数正则化参数λ，TSDEC算法的聚类准确度优于其它3种算法。当正则化参数λ越大时，TSDEC算法的聚类准确度越接近于EDEC算法，这验证了TSDEC算法是EDEC算法的广义形式，且当正则化参数λ趋于无穷大时，EDEC算法成为TSDEC算法的特例。

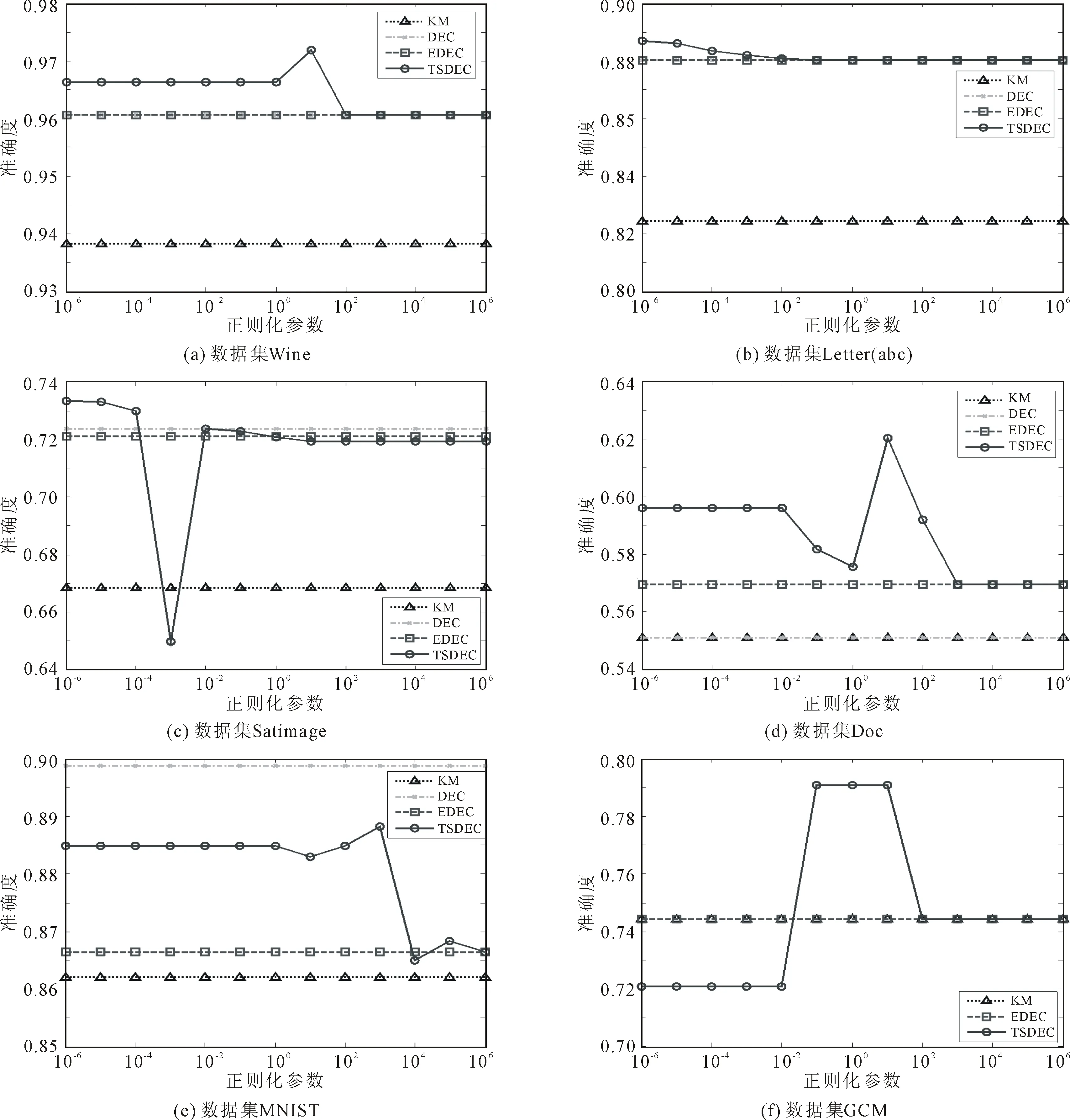
图1各数据集聚类结果

不同正则化参数下的最优聚类准确度及平均聚类准确度结果如表2所示。其中，“—”表示DEC算法在相应参数下内存溢出。

由表2可知，在大多数数据集上，TSDEC算法的最优聚类准确度及平均聚类准确度优于KM算法、DEC算法EDEC算法。

表2 4种算法在6组数据集上的聚类准确度

3.3 运行时间测试

4种算法对6个数据集在不同正则化参数取值下的运行时间如图2所示。其中，DEC算法在GCM数据集上运行内存溢出，无法获得运行时间，而KM算法、DEC算法和EDEC算法的运行时间各是一条不随正则化参数λ变化的直线。

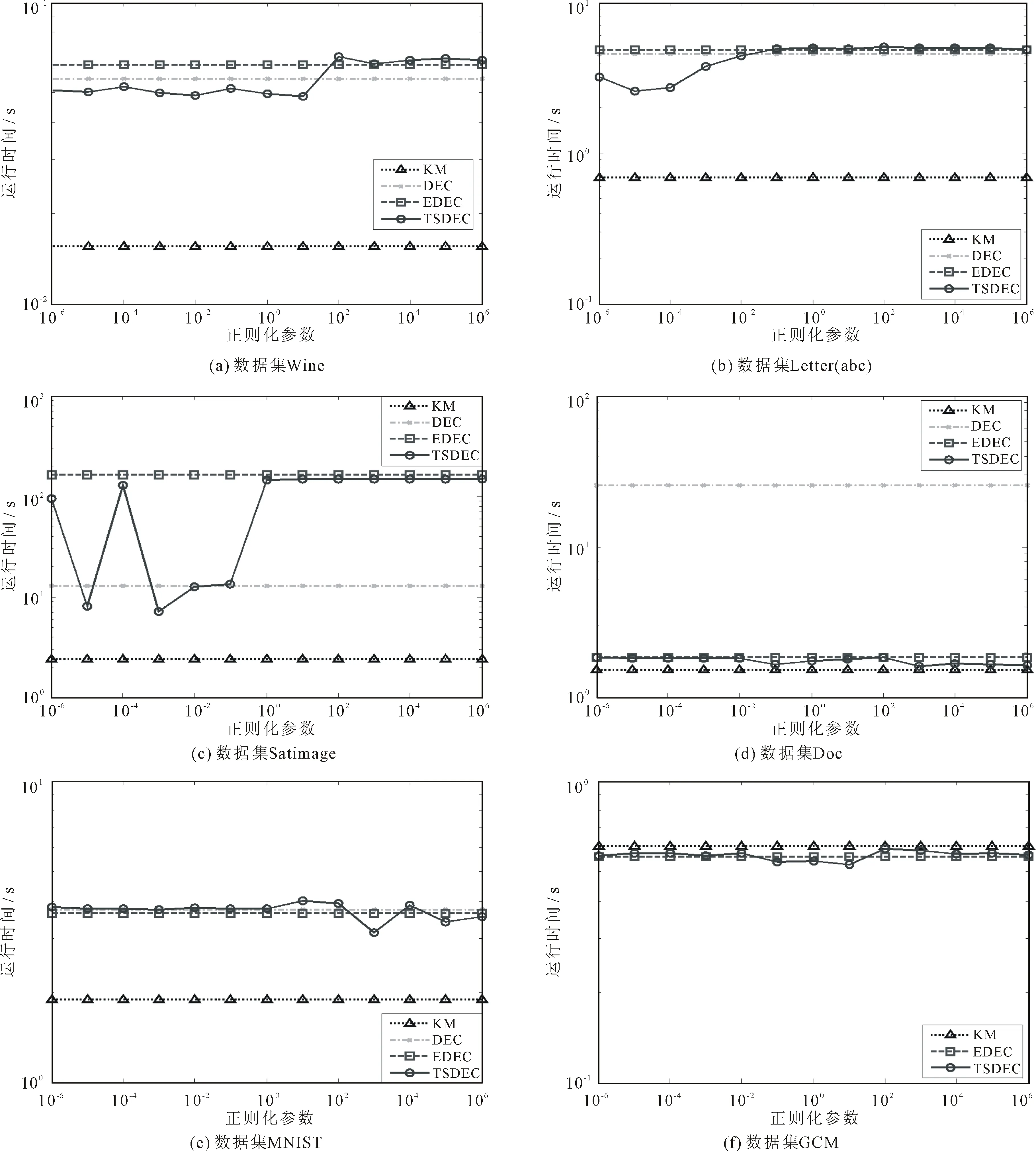
图2 各数据集上4种算法的运行时间

由图2可知，除了GCM数据集，KM算法在其它数据集上的平均运行效率最高，运行时间是4种算法中最少的，但聚类准确度相较于其它算法有所偏低。TSDEC算法与EDEC算法的运行效率基本持平，且当正则化参数λ越大时，TSDEC算法的运行时间越接近于EDEC算法。对于两个高维数据集DOC和GCM而言，TSDEC算法和EDEC算法的运行效率明显优于DEC算法。

各数据集在不同正则化参数下的最优聚类准确度和平均聚类准确度相对应的运行时间如表3所示。其中，To和Tm分别表示各算法的最快运行时间和平均运行时间， “—”表示DEC算法在相应参数下内存溢出。由表3可知，除KM算法外，在大多数数据集上，EDEC算法的平均运行效率较高，而TSDEC算法的最优运行效率相较于DEC算法和EDEC算法有所提高。

表3 4种算法在6组数据集上的运行时间

4 结语

TSDEC算法通过对正则化的类间散度矩阵做奇异值分解，得到数据的降维预处理，再对降维后数据进行判别嵌入式聚类，可以看作是在EDEC算法中引入类间散度矩阵正则化过程所得到的一般性算法。TSDEC算法将DEC算法的主要时间复杂度由O(nm2)降低为O(nmc)。实验结果表明，正则化过程的引入提高了原EDEC算法对数据的适应能力。对大多数的数据集而言，TSDEC算法的聚类准确度(包括平均准确度和不同参数下的最优准确度)优于DEC与EDEC算法。TSDEC算法的运行效率与EDEC算法相当，对于高维数据集，二者的运行效率均优于DEC算法。TSDEC为线性聚类算法，为了提高算法对非线性可分数据的聚类性能，下一步的工作是利用核技巧[19]给出TSDEC算法的核版本。