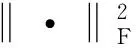基于稀疏自表示的模糊聚类图像分割算法

张宝军, 张丽丹, 吴成茂, 田妮花

(1. 西安邮电大学 电子工程学院, 陕西 西安 710121; 2.中国石油庆阳石化公司, 甘肃 庆阳 745002)

图像分割[1-2]是图像处理和计算机视觉领域中的核心研究内容，图像分割的好坏直接影响图像分析、识别等其它后续工作。

图像分割的方法很多，其中模糊C均值(fuzzy C-means，FCM)聚类算法[3-4]被广泛应用于图像分割，但其只考虑到图像的灰度信息，未考虑到邻域像素的相关性，致使算法对噪声的鲁棒性差，分割效果不理想[5]。空间约束模糊C均值(fuzzy C-means with spatial constraints，FCM_S)聚类算法[5]将像素邻域空间信息加入到FCM算法的目标函数中，抗噪性能有一定的提高，但增加了算法的迭代次数和聚类时间，其改进算法FCM_S1和FCM_S2[6]分别用邻域矩阵的均值和中值代替FCM_S算法中邻域像素，降低了算法的计算复杂度，前者对高斯噪声有很好的鲁棒性，但对椒盐噪声的效率较低；后者对椒盐噪声有较好的抑制作用。增强模糊C均值(enhanced fuzzy C-means，EnFCM)聚类算法[7]和快速广义模糊C均值(fast generalized fuzzy C-means，FGFCM)聚类算法[8]通过构建权值和图像，以图像的灰度级来代替像素点进行聚类分割，提高了分割效率，但在聚类过程中丢失图像的部分细节，降低了图像的聚类精度[8]。模糊局部信息C均值(fuzzy local information c-means，FLICM)聚类算法[9]利用无参数模糊因子控制图像噪声和图像细节之间的平衡，但这种算法只考虑局部邻域信息，对复杂图像特别是受强噪声污染图像，尚未达到理想的分割效果。

现有的模糊聚类算法没有考虑到图像的全局结构信息，多数模糊聚类算法中的聚类数据只描述了一种表示图像样本的基本物理性质，如位置，大小和灰度等，没有反映样本间的相关性。样本的类内相似性和类间差异性有助于聚类。若知道每个样本在样本集中所发挥的作用，将相似样本划分为同一类，有助于实现理想的聚类结果。样本的结构不可预测，但通过稀疏表示(sparse repreaentation, SR)方法[10-15]可以挖掘出反映全局结构中任意样本之间的相关性。

为了提高噪声污染图像分割的鲁棒性，本文拟将包含样本数据集全局结构信息的SR技术和经典的FCM算法相结合，提出一种基于稀疏自表示的模糊C均值聚类(fuzzy C-means clustering based on sparse self-representation, SSR_FCM )的图像分割算法。不同于传统的FCM算法基于图像的灰度值实现图像分割，本文算法以超像素为基元，提取超像素特征构成图像特征矩阵，通过稀疏自表示的方法找出表示样本间相关性的系数矩阵，作为图像的判别特征，利用FCM算法对该判别特征分类，实现图像分割。对不同类型的图像添加高斯噪声和椒盐噪声，比较算法分割后的峰值信噪比(peak signal to noise ratio, PSNR)，验证算法的抗噪鲁棒性。

1 模糊C均值聚类算法

模糊C均值聚类算法通过最小化目标函数将数据集划分成不同的类，其目标函数可描述为

(1)

约束条件为

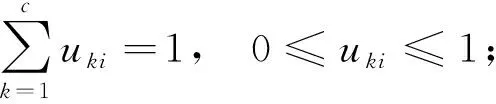
其中，

Y={yi;i=1,2,…,n}

是待分割图像，n为像素个数，yi表示第i个像素的灰度值；

V={vk,k=1,2,…,c}

表示区域的聚类中心，c为聚类个数，vk表示第k个类别的聚类中心；

d(yi,vk)=‖yi-vk‖

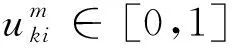
根据模糊C均值聚类算法，目标函数利用拉格朗日乘子方法得到隶属度函数和聚类中心，分别为U={uki}和V={vk}，更新迭代公式为

(2)

(3)

利用式(2)和(3)分别更新隶属度矩阵和聚类中心，直到算法收敛；然后采用最大隶属度方法将像素i分配到对应类别中，完成图像的分割。

2 基于稀疏自表示的模糊C均值聚类算法

2.1 建立稀疏自表示模型

稀疏表示是将样本表示为预先规定的字典中的少数原子的线性组合。以样本数据本身作为字典，对于每个数据点都可以被除它之外的数据点线性表示，这种构造字典的方式称为稀疏自表示[16]。该方法能够反映出数据之间的相关性，同时也避免了构建字典过程中的计算复杂度。稀疏自表示的目标模型[12]

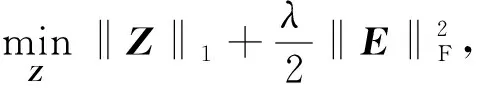
(4)

其中，样本的基本特征矩阵

X=[X1,X2,…,Xn]∈a×n,

n为样本数，xi(i=1,2,…,n)表示第i个样本的具有a维属性的特征向量(1≤a≤n)。‖·‖1为L1-范数，即

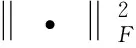
Z=[Z1,Z2,…,Zn]∈n×n

为X的稀疏自表示系数矩阵；参数λ>0用来平衡式(4)中的权重，diag(Z)=0表明每一类样本都不能将自身作为相关性样本。本文算法中，图像以超像素为基元，选择合适的超像素特征，X为所有超像素特征构成的基本特征矩阵，n为超像素块数，Xi代表一个超像素的a维特征向量。该模型应用于被噪声干扰的数据中。

利用交替方向乘子法(the alternating direction method of multipliers, ADMM)[17]对(4)式进行求解。

消除目标函数中的E，等价于求解

适当引入辅助变量，将约束增加到目标函数中。

首先，引入辅助矩阵H，式(4)可以改写为

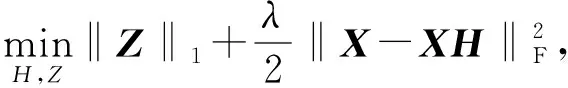
其次，引入矩阵W∈Rn×n拉格朗日乘子，构造拉格朗日函数

式中μ为惩罚因子，〈·〉表示标准内积。

最后，给出交替方向乘子法实现稀疏自表示系数实现的具体步骤如下。

步骤1输入X，参数λ。

步骤2初始化

H(0)=0,Z(0)=0,W(0)=0,
η=10-3,μ=10-4,ε=1.1,k=0。

步骤3更新

步骤4更新

H(k+1)=J-diag(J)。

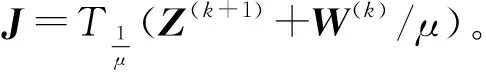
步骤5更新

W(k+1)=W(k)+μ(Z(k+1)-H(k+1))。

步骤6更新

μ=min (εμ, 1010)。

步骤7判断是否有‖H(k)-Z(k)‖∞≤η,并且‖H(k)-H(k-1)‖∞≤η,如果满足条件，则算法迭代结束，否则返回步骤3。

步骤8输出最优稀疏自表示系数矩阵Z。

2.2 构造目标函数

稀疏自表示系数有较好的类别区分性能，可以作为图像的判别特征，将矩阵Z表示为图像的判别特征矩阵。利用模糊C均值聚类算法聚类图像的判别特征矩阵,将其代入式(1)中，目标函数、隶属度函数和聚类中心分别描述为

(5)

(6)

其中，Zj=[Z1,Z2,…,Zn]∈Rn×n为图像的判别特征矩阵，n为样本数；Z=[Zj1,Zj2,…,Zjn]表示Z的第j列，是图像基本特征矩阵X的线性表示；c是聚类中心数(10。

利用式子(5)和(6)分别更新隶属度和聚类中心，直到算法收敛；将判别特征Z中的每个样本分配到对应类别中。

2.3 本文算法步骤

本文算法主要步骤，如图1所示。

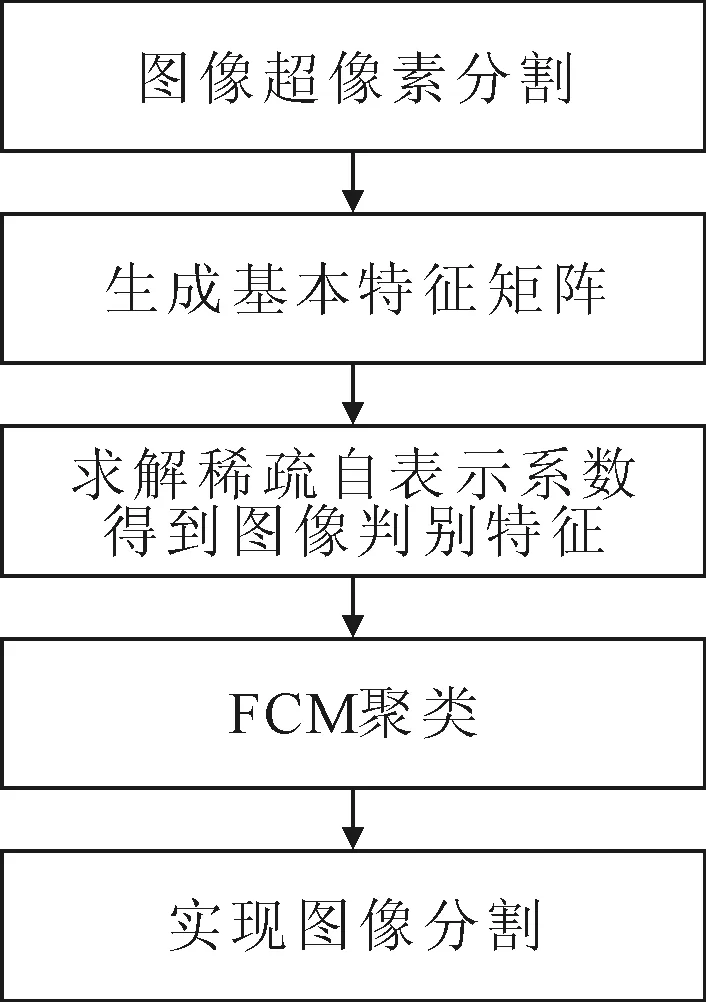
图1 算法主要步骤

图1中，在对图像过分割生成超像素时，对超像素做标记，图像像素点的标签值与所属的超像素标签值相同，在FCM算法中采用最大隶属度方法将判别特征Z中稀疏自表示系数Zj(1≤j≤n)分配到对应类别中，若Zj隶属于第p类(1≤p≤c)，则标签值为j的超像素中的像素点也隶属于第p类，从而实现图像分割。

3 实验结果及分析

选取合成图像、自然图像和遥感图像，验证算法对受噪声污染图像分割的鲁棒性，比较改进算法与FCM，FCM_S，EnFCM，FGFCM，FLICM五种算法对待分割图像的分割结果。其中实验运行环境为Matlab.R2014.b，对所有的比较算法，共同设置模糊加权指数m=2，迭代终止条件ε=0.000 1，局部邻域窗口的大小为3×3。

对于FCM_S和EnFCM算法，邻域信息对中心像素的影响因子α=2。FGFCM算法[8]中控制邻域信息对聚类结果影响程度的各个参数均采用文献[8]的设置。改进算法中，首先对原始图像使用Turbopixels算法[18]进行超像素分割，替代单个像素作为图像基元，对Turbopixels算法的分割尺度设置为600，提取超像素的灰度均值和灰度直方图2种特征量生成一个统一整体特征作为图像的基本特征矩阵。

3.1 算法鲁棒性测试与分析

选取自然图像、遥感图像和人造图像3幅灰度图像，对其添加不同均方差的高斯噪声和不同强度的椒盐噪声，利用FCM、FCM_S、ENFCM、FGFCM、FLICM以及本文算法对其进行分割测试，采用峰值信噪比[19](peak signal to noise ratio, PSNR)作为图像分割算法抗噪性能好坏的评价指标。PSNR值越大，表明分割算法抗噪性越好。

3.1.1 高斯噪声干扰图的分割结果及分析

选取遥感图像，人造图像，鲜花图像，如图2所示。其分别添加均值为0且方差为0.1、0.08、0.15的高斯噪声。采用FCM算法、FCM_S算法、ENFCM算法、FGFCM算法、FLICM算法以及改进算法对加噪图像进行分割测试，测试结果如表1和表2 所示。

图2 标准灰度图像

图像加噪灰度图FCM算法FCM_S算法ENFCM算法FGFCM算法FLICM算法改进算法遥感图人造图鲜花图

表2 不同算法抗高斯噪声的PSNR值

由表1和表2可见，改进算法与另5种算法相比，差异显著；FCM算法去噪和分割能力较差，加入邻域信息的FCM_S算法、ENFCM算法、FGFCM算法和FLICM算法比FCM算法效果好；本文的改进算法将稀疏自表示技术嵌入到FCM算法中，所得去噪效果和分割效果优于其他5种算法。

3.1.2 椒盐噪声干扰图的分割结果及分析

针对遥感图像、人造图像和飞机图像，如图3所示。分别添加强度为15%、20%、30%的椒盐噪声，采用FCM算法、FCM_S算法、ENFCM算法、FGFCM算法、FLICM算法和本文算法进行分割测试，测试结果见表3和表4所示。

图3 标准灰度图像

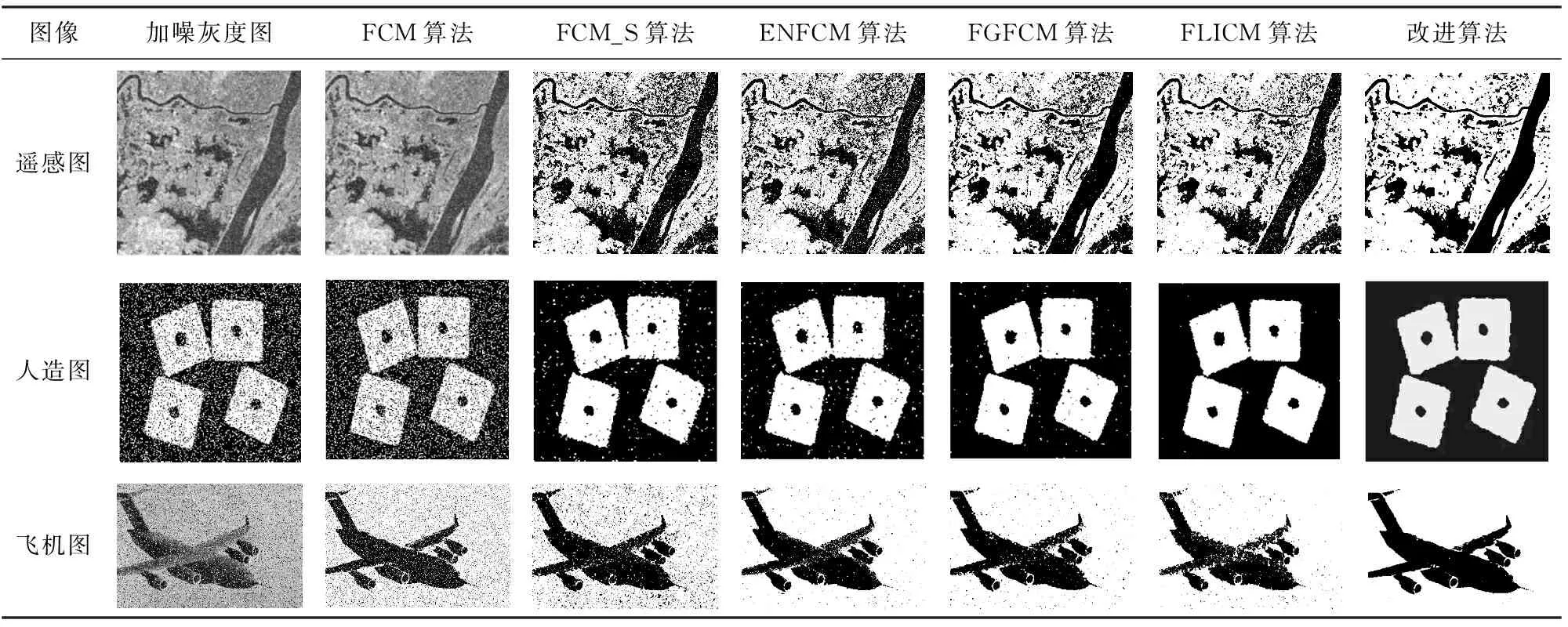
图像加噪灰度图FCM算法FCM_S算法ENFCM算法FGFCM算法FLICM算法改进算法遥感图人造图飞机图

表4 不同算法抗椒盐噪声的PSNR值

由表3和表4可见，在视觉效果上，改进算法的抗噪能力优于其他5种算法；FCM_S算法、ENFCM算法、FGFCM算法和FLICM算法在一定程度上去除了噪声点，但图像的分割结果中仍含有大量噪声，改进算法获得的分割结果几乎可以完全去除噪声。相比其他5种算法，本文算法将飞机模型从背景中完整提取，且提取出的飞机图像较为清晰、边缘轮廓较为完整；对于遥感图中的河流能够准确地区分河流信息和背景信息。

由以上实验分割图的视觉效果和相关数据分析可知，对于噪声污染的图片，传统的FCM算法像素点间没有联系，对噪声较为敏感，分割结果最差。FCM-S算法、ENFCM算法、FGFCM算法和FLICM算法建立在空间邻域信息的基础上，分割结果比传统的FCM算法好，但对于图像中加入不同强度的高斯噪声和椒盐噪声，分割后的图中依旧留有大量噪声。改进算法中稀疏自表示模型中通过2个范数的约束不仅能得到样本间的相关性表示，有利于相似样本分为同一类，而且对包含噪声的数据有鲁棒性，增强聚类效果；在基于反映样本间相关性和鲁棒的判别特征上聚类，清晰地判别出图像分割类数，虽然聚类结果没有完全去除噪声，但去除了大部分噪声，取得较好的分割结果。

3.2 保真项参数λ分析

接着来讨论改进算法稀疏自表示模型中的保真项参数λ的选取。如图2(b)所示的人造图像是分辨率为256×230的三类灰度图像，灰度值分别为0，195和255。测试人造图像受到均值为0，方差为0.1的高斯噪声影响下的正确分割率[20]，为保证数据的准确性，正确分割率采用算法15次运行结果的均值，不同保真项参数λ值对应的分割正确率，如图4 所示。

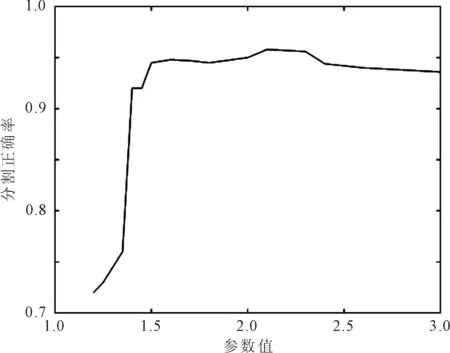
图4 不同保真项参数λ的分割正确率

通过图4可以看出，曲线在一小段波动后趋于平稳。当λ≥2时，分割正确率明显提高，表明参数λ在稀疏自表示模型中有重要作用。此外，当λ较大时，分割正确率缓慢下降，这是因为式(4)中第2项的作用不能被无限放大，第1项的稀疏约束对算法也起到了作用。

4 结语