二阶线性微分方程不变量解法的新类型

赵临龙

(安康学院数学与统计学院，陕西 安康 725000)

对于变系数线性微分方程的可积性，尽管从理论上，完成了其解的构造.即线性微分方程L(x)＝f(x)的通解，由其对应的齐次线性微分方程L(x)＝0的通解和对应的非齐次线性微分方程L(x)＝f(x)的特解构成.但齐次线性微分方程的通解和对应的非齐次线性微分方程的特解，怎样来求?至今仍然是世界难题[1].近3年，有关二阶线性微分方程的可积性的文献不少[2-21].

1 问题背景

具有普遍性的还是二阶线性微分方程的不变量解法.

1997年，赵临龙给出二阶齐次线性微分方程的不变量解法[22]，引起人们注意，被文献引用[23-30].

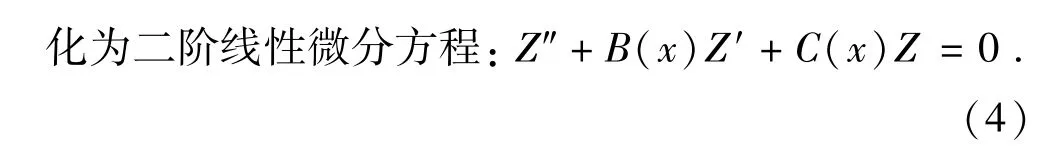
于是，二阶方程有可积类型：

①对于常数b，c，当B(x) ＝ b，C(x) ＝ c时，有可积的常系数方程：Z″+bZ′+cZ ＝0.

②对于函数B(x)和C(x)，当C(x)＝0时，有可积的降阶方程：Z″+B(x)Z′＝0.

1998年，赵临龙再次将该方法引入二阶非齐次线性微分方程，给出不变量解法[30].引起更多人们的注意，被文献引用[31-42].

由于 Riccati方程不一定可积，因此对于方程(5)，往往无法通过 Riccati方程(6)，求得函数B(x).这需要给出新的不变量关系式，以及二阶线性微分方程的可积类型.

2 可积新类型

当方程(15)可积时，就可求得方程(5)的解.对于二阶变系数性微分方程(1)，有可积类型.

3 应用

由定理4的结论⑤：p(x)+q(x)x＝2x-2x＝0，得到方程的一个解z＝x.

由定理4的结论③：取φ(x)＝mx(m待定)，则2mx-2x+(m+m2x2-2mx2-4)x＝0，即3(m-2)+m(m-2)x2＝0.求得：m ＝2.

得到方程(20)的一个解 z ＝ xe∫φ(x)dx＝ xe∫2xdx＝xex2.

于是，方程(20)通解为z＝c1x+c2xex2.

由定理3，得到原方程的通解：

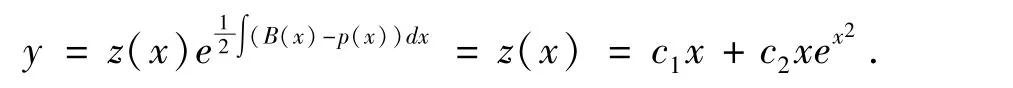
例2[15]求解二阶变系数齐次线性微分方程y″-xy′+(2x-4)y ＝ 0.

这是不同原文的新解法.

该解法丰富了原文解法.这正是不变量解法的优越性.