铝合金桅杆结构强度和振动计算分析

王燥春，马晓峰，陈 吉

（沪东中华造船（集团）有限公司，上海 200129）

0 引 言

某加改装项目需加装作战系统，因而需增加通信、雷达等多种特种设备，原船桅杆无法满足其设备布置要求，需重新设计桅杆；同时，项目的总体性能要求尽可能降低上层建筑的重心，改善船舶稳性。桁架式铝合金桅杆具有重量轻、受风面积比封闭式桅杆小等优点，因此将该项目中的桅杆设计成桁架式铝合金结构。

本文在计算载荷时综合考虑风载荷和惯性载荷的叠加作用，通过对新设计的桅杆进行结构强度和振动的有限元计算分析，验证桅杆结构形式的合理性，对桁架式桅杆结构的有限元计算具有重要的参考意义。

1 桅杆结构有限元模型

1.1 有限元模型

对于整个船体结构而言，桅杆结构受力属于局部强度问题。根据圣维南原理，为尽量降低边界条件对计算结果的影响，对模型范围进行适当扩充[1]，取整个桅杆结构及桅杆下一层甲板结构作为模型范围。

桅杆是一个桁架结构，包括主桅、顶桅和侧桅，采用6082-T6铝合金管和5083-H116铝合金板制造，其中铝合金管规格主要为φ114mm×6mm、φ89mm×5mm和φ60mm×4mm，雷达平台主要为8mm铝合金板。在建立有限元模型时，可用梁单元按自然节点进行离散，平台等结构运用壳单元进行离散。图1为桅杆结构有限元离散模型，该模型有920个节点、1243个单元。

1.2 边界条件

1.3 结构材料属性

铝合金的材料属性为：弹性模量 E =0.7×105MPa；泊松比为0.3；密度为2.7×103kg/m3；屈服极限sσ=260MPa，焊后为125MPa。

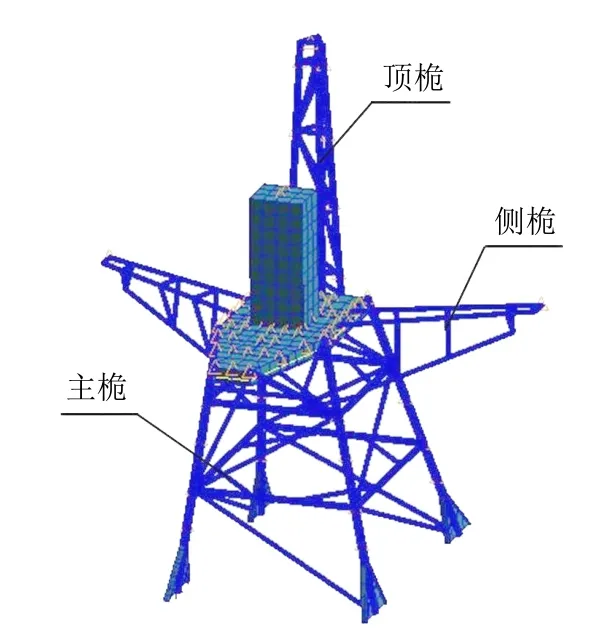
图1 桅杆结构有限元离散模型

1.4 许用应力

根据《水面舰艇结构设计计算方法》[2]19.3.3的规定，校核桅结构强度的许用正应力和许用剪应力的计算式为

式(1)和式(2)中：sσ为材料的屈服极限，取焊后125MPa；[σ]为许用正应力，MPa；[τ]为许用剪应力，MPa。

2 计算载荷

根据《舰船通用规范》[3]（以下简称《规范》），水面舰艇在波浪上航行时，其桅杆结构除了承受自身结构和设备的重量所引起的重力以外，还承受风压力及舰船摇摆时产生的惯性力，因此在计算时需综合考虑风载荷及横摇和纵摇时的惯性载荷。

在进行强度分析时，取最严重的载荷组合，即将风载荷、惯性载荷和重力载荷迭加起来。

2.1 风载荷计算

风载荷的计算式为

式(3)中：PW为风压，按无限航区取1.96kN/m2；AW为受风面积（在横摇和纵摇状态下分别计算），m2。

2.2 惯性载荷计算

根据《规范》，在进行强度计算时应使舰船处于最大纵摇或横摇状态下，并应符合《水面舰艇结构设计计算方法》[2]中的相关规定。

2.2.1 横摇惯性力计算

图2为横摇工况下结构的应力分布。在横摇时，对于图2所示的坐标系，桅杆在各坐标轴方向上的惯性力的计算式为

式(4)中：M为设备的质量，kg；Tφ为船的横摇周期，s；φmax为船的最大横摇角，以主甲板甲板边线入水角记，rad；r为船的重心轨迹半径，，m；Z为设备重心与船重心之间的高度差，m；Y为设备重心到船中的横向距离，桅杆布置在船中，故取0。

2.2.2 纵摇惯性力计算

图3为纵摇工况下结构的应力分布。在纵摇时，对于图2所示的坐标系，桅杆在各坐标轴方向上的惯性力的计算式为

式(5)中：M为设备的质量，kg；Tθ为船的纵摇周期，s；θmax为船的最大纵摇角，rad；Z为设备重心与船重心之间的高度差，m；X为设备重心到船中的纵向距离，桅杆布置在船中，故取0。

2.3 重力载荷计算

桅杆和设备重力的计算式为

式(6)中：M为设备的质量，kg；θmax为船的最大纵摇角；φmax为船的最大横摇角。

3 桅杆结构强度分析

3.1 整体有限元分析

分别在横摇和纵摇2种工况下对图1所示的有限元模型进行强度分析，得出对应工况下结构的应力分布（见图2和图3），计算结果见表1。由图2和图3可知，最大的应力发生在横摇工况下顶桅与主桅相交的单根支撑杆上，σmax=16.3MPa，小于许用应力[σ]=56.3MPa，满足强度要求。

表1 桅杆应力计算结果 单位：MPa

图2 横摇工况下结构的应力分布

图3 纵摇工况下结构的应力分布

3.2 局部细化有限元分析

由于桅杆的4根支撑需承受全部载荷并将其传递到主船体上，从安全角度考虑，需对桅杆支撑脚及其附近船体结构作细化有限元分析。为此，以桅杆某一支柱为中心，将其附近 1.65m×1.42m×2.35m范围内的船体结构作为分离体，用壳板单元和梁单元进行离散。

分离体有限元模型有35215个节点、36582个单元，细化处单元的尺寸为6mm×6mm，与桅杆支撑脚壁厚和桅杆下船体结构板厚相同。

载荷采用总体计算所得的桅脚剖面的位移：

1) 在横摇状态下，剖面在x轴、y轴、z轴方向上的位移分别为0.058521，1.125650，-0.064580；

2) 在纵摇状态下，剖面在x轴、y轴、z轴方向上的位移分别为1.052640，0.036850，0.045256。

边界节点采用自由支持边界条件，即：Ux=Uy=Uz=0。

通过对分离体模型进行强度分析，得到横摇和纵摇状态下的应力分布见图4和图5。由图4和图5可知，横摇工况和纵摇工况的最大应力σmax分别为31.5MPa和40.2MPa，小于6082-T6牌号铝合金材料的焊后屈服极限σs= 125MPa，满足强度要求。

图4 横摇工况下桅脚结构的应力分布

图5 纵摇工况下桅脚结构的应力分布

4 桅杆结构振动分析

4.1 主要激励源

4.1.1 主机

该船主机的型号为MTU16V595T90，主机激励频率见表2。

表2 主机激励频率 单位：Hz

4.1.2 螺旋桨

该船配置的螺旋桨为 3台4叶桨，相应的激励频率见表3。

表3 螺旋桨激励频率 单位：Hz

4.1.3 船体总振动激励

总振动激励频率为船体梁总振动自有振动频率，通过总振动分析得：

1) 一阶垂向振动自振频率范围为3.20～3.34Hz；

2) 二阶垂向振动自振频率范围为7.21～7.50Hz。

4.2 结构振动有限元分析

通过对图1所示的有限元模型进行振动分析，得到桅杆的固有频率（见表4）和模态。

《规范》要求，桅杆纵向、横向和扭转振动的第一谐调固有频率计算值应避开主机和螺旋桨激振频率及船体固有频率。

由计算结果可知，桅杆固有频率避开了主机二阶激励频率和螺旋桨轴频、叶频激励频率，避开了舰船总体自振频率；桅杆固有频率与主机一阶激励频率错开百分比见表5。

表4 桅杆固有频率 单位：Hz

表5 主机一阶与桅杆横向、纵向、扭转第一谐调错开百分比 单位：%

5 结 语

根据《规范》，结合加改装项目的实际情况，通过采用有限元计算分析方法对横摇、纵摇等状态下的桁架式铝合金桅杆进行结构强度和振动校核，得到以下结论：

1) 通过对桅杆结构强度进行有限元计算分析，特别是对桅脚进行细化网格分析可知，桅杆的结构强度满足《规范》的要求。

2) 通过对桅杆进行振动分析，得到了桅杆结构的纵向、横向和扭转振动固有频率计算值，该频率避开了主机激励频率、螺旋桨激励频率和舰船总体自振频率，满足《规范》的要求。

3) 根据桅杆振动分析结果，桅杆扭转第一谐调固有频率与主机进三的一阶激励频率错开较少。由于主机一阶激励力非常小，一般不会激起大的振动，但需要时可根据实际情况，例如通过桅杆振动试验，适当调整进三转速，使桅杆扭转第一谐调固有频率与主机进三的一阶激励频率错开百分比扩大，改善桅杆振动状况。

通过有限元分析对桁架式桅杆结构振动进行计算的案例较少，本文的计算方法可为以后桁架式结构的振动预报分析提供参考。