耦合加载方式下复合材料叶片的预应力模态分析*

郑玉巧 曹永勇 张亮亮,2 王志远,2

(1.兰州理工大学 机电工程学院, 兰州 730050)(2.东方电气风电有限公司, 德阳 618000)

引言

风能是一种储量巨大的环保可再生能源,因此,在全球各国新能源市场中风能占据了空前绝后角色.开发风力发电对调整整个能源结构、解决传统化石燃料危机及减小环境污染等方面有着非常重大的意义.风力机风轮是由叶片和轮毂组成的用来捕捉风能的重要构件[1-3],并将捕捉的风能转化为机械能,最后转变为电能输出.据英国凯斯内斯风电场信息论坛(CWIF)[4]统计,因叶片失效导致的事故2006年17起,2010年20起,2012年28起,2013年35起,2015年19起,2016年20起,这些事故给国家和社会的经济造成了巨大损失.在此环境下,对风力机叶片在静止与旋转过程中各阶模态有必要准确模拟研究并找出其变化规律[5-8],探讨影响叶片模态的重要因素,这样对于抑制叶片共振造成的经济损失具有重大意义.

针对风力机叶片振动问题,国内外众多学者已开展了诸多相关研究.Gangele[9]基于有限元法探讨了材料属性对叶片固有频率的影响.苏东[10]在风力机叶片满足工作环境工况下,通过获取叶片的气动压力,对叶片进行了预应力模态分析.安利强[11]研究了梁帽铺层参数和主梁形式对叶片固有频率的影响.陈文朴[12]基于气动弹性剪切条件下,研究了铺层参数对叶片动态特性的影响.风力机叶片是一种大型细长弹性构件[13,14],受空气动力、重力及自身惯性力等动态交变载荷的作用[15].由于所受载荷的交变形和随机性,使得弹性叶片极易产生振动,当弹性叶片的固有频率与激振频率相同时便会发生共振[16],共振使得叶片发生疲劳断裂.风力机正常工作过程中,在空间绕其旋转轴做大范围旋转运动,叶片的旋转运动和弹性变形之间的相互耦合作用将导致叶片刚度增大,这一现象被称为预应力效应[17,18],这给叶片的动力学研究和数值计算分析研究带来了巨大困难.本文运用多体系统动力学方法,采用耦合加载方式将叶片稳态工况下所受载荷加载到叶片扭转中心,并赋予叶片一定旋转速度模拟风机实际运转,预应力效应下对叶片进行了振动特性分析,探讨了预应力效应对叶片振动特性的影响、考察了固有频率对预应力效应的敏感程度,研究了转速对叶片频率的影响变化规律.

1 动力学模型

动力学方程是解决结构振动的核心问题.叶片固有频率作为叶片的固有特性,仅与叶片的质量矩阵和刚度矩阵有关,因此,计算过程中忽略了阻尼的存在.利用“弹簧—质量”系统来研究风电机组叶片的动力学问题.其中,单位长度叶片动力简化模型如图1所示.

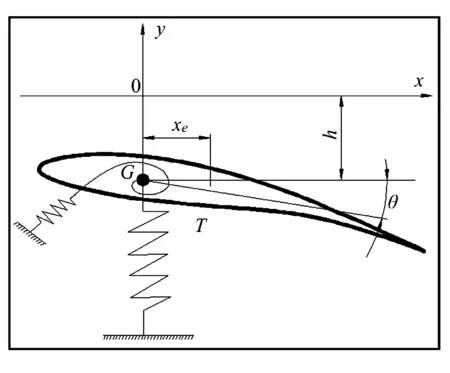
图1 单位长度叶片动力模型Fig.1 Simplified dynamic model of unit-length blade

根据瞬时最小势能原理,建立叶片动力学方程为：

(1)

在研究叶片的固有动力特性时,工程上一般不计入阻尼作用,于是式(1)可写为：

(2)

设式(2)的解为：

{x}={X}sinωt

(3)

将式(3)代入式(2)可得：

([K]-ω2{M}){X}={0}

(4)

令ω2=λ,则：

([K]-λ{M}){X}={0}

(5)

要使式(5)有解,则必须满足：

det([K]-λ{M})

(6)

叶片的n阶固有频率可表示为：

(7)

实际运转工况下,叶片受重力、离心力与气动力等共同作用,将风速引起的气动载荷与转速引起的离心力作用于叶片上,产生预应力效应,此时叶片的振动方程为：

(8)

有限元求解过程中,将叶片的实体单元进行划分处理,其任一单元的预应力矩阵[S]可表示为：

(9)

其中,

(10)

(11)

(12)

2 叶片模型的建立

2.1 技术参数

叶片内部采用双腹板梁空心结构,主要由内外蒙皮、主梁、腹板等组成.风轮由三叶片和轮毂构成,其中,风轮直径83m,叶片长度40.5m,展向18.5%位置处达最大弦长3.198m,额定转速17.2rpm,切入风速4m/s,切出风速25m/s,塔架高度65m,采用变速发电机和变速变桨控制方式.

2.2 有限元模型

将三维造型软件UG中建立的叶片实体模型以.IGS文件格式导入到有限元分析软件ANSYS中,叶片采用3D壳单元SHELL181进行建模,单元形状为四面体形状,该单元具有非线性稳定、收敛速度快等诸多优点.采用平面切割方式对叶片在展向和弦向进行区域划分,将叶片分成不同的区域,然后通过定义各区域的铺层材料属性、铺层方式、铺层角度及铺层厚度,建立精确地叶片有限元模型,如图2所示.因叶片叶尖部分弦长相对展向内其余弦长较小,同时厚度相对也较薄,故建模时忽略了叶尖建模.为建立连续铺层,实际铺层中将中断层厚度设置为零,所建叶片有限元模型具有321个面,共包括单元数35387个,节点数34282个,不同颜色代表不同的铺层方式和铺层厚度.

图2 叶片有限元模型Fig.2 Finite element model of blade

3 预应力模态分析

预应力模态分析时叶片的预应力主要来自于由风速引起的气动载荷、重力及转速引起的离心力.因此,首先采用德国GL标准[19]认证的风力机设计软件GH BLADED,计算了稳态工况时额定风速下叶片各截面所受载荷(见表1).

表1 额定风速下叶片所受载荷Table 1 Loads of blade at the rated wind speed

将叶片的扭转中心视为载荷作用点,该作用点与翼型截面周围的所有节点通过刚性耦合进行固结,从而将作用于扭转中心的载荷耦合加载到叶片分析模型上,这种加载方式较常规加载方式,更能够真实地反映叶片的受力情况,依据叶片静力测试实验的载荷加载方式,选取距叶根15m,21m,25.5m,30m,34.5m五个不同位置作为载荷加载部位,各截面载荷耦合效果及展向方向载荷加载部位如图3所示.当载荷加载完成后,对叶片结构进行静力学分析,结构静力学分析得到的应力分布结果如图4所示.

图3 耦合效果及载荷分布Fig.3 Coupling effects and loads distribution

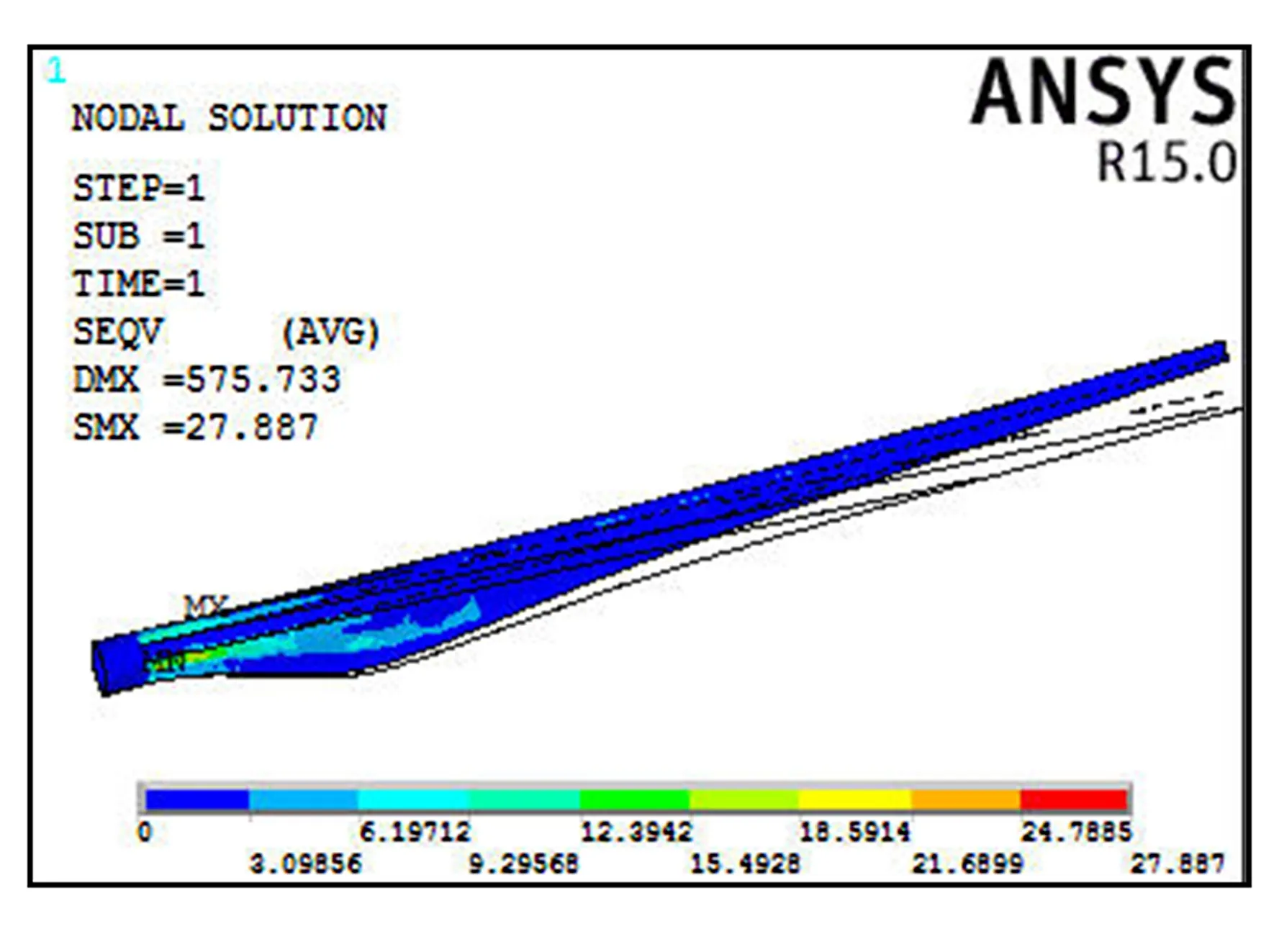
图4 叶片等效应力云图Fig.4 Equivalent stress contour of blade

Lanczos法由于具有收敛速度快、求解精度高等诸多优点,目前在求解大型特征值问题中被认为是最有效的方法,故本文选取分块Lanczos方法求解.基于叶片静力分析时所得应力结果,进一步对叶片进行预应力模态分析,由式(9)计算得到叶片的预应力刚度矩阵,然后根据式(8)将其叠加到模态刚度矩阵上,计算得到预应力效应下叶片的各阶固有频率和振型.根据振动理论,低阶振动频率比高阶振动频率更危险,因此前几阶振动对叶片的动力学性能影响较大,故本文只选取叶片前八阶模态进行分析研究.

表2给出了无预应力效应时叶片的前八阶固有频率和振型.从表2中可以看出,挥舞和摆阵弯曲运动是叶片振动的主要振型,且随着固有频率的不断增大,叶片的振动形式也逐渐变得复杂,高阶振型便是挥舞、摆阵及扭转运动的耦合振型.额定转速17.2rpm下,叶片的一阶固有频率0.47Hz(28.2rpm),与风轮额定转速相差64%,因此该叶片设计满足结构动力学基本设计要求.

表2 叶片固有频率及振型Table 2 Natural frequency and modes of blade

表3 预应力效应对固有频率的影响Table 3 Effect of pre-stressing effect on natural frequency

表3给出了预应力效应下叶片在转动角速度分别为：0 s-1、0.9 s-1、1.8 s-1、3.6 s-1、5.4 s-1、7.2 s-1时,叶片的前八阶固有频率.从表3中可看出,预应力效应下叶片的振动频率随转速的不断增大而增大.在额定转速下(17.2rpm,即1.8s-1)风轮运转时,预应力效应对叶片的固有频率有较大的影响,叶片一阶频率从0.47Hz变为0.57Hz, 相应地二阶频率由1.03Hz变为1.12Hz.由此可见,预应力效应使得叶片的固有频率变大,这主要是由于预应力效应使得叶片的整体刚度增强.预应力效应下,研究转速对叶片模态的影响变化规律,这里仅给出额定转速下叶片的前八阶模态振型,如图5所示.

图5 叶片前八阶振型Fig.5 The first eighth order modes of blade

从图5可以看出,挥舞方向叶片首先发生了振动,接着摆阵方向发生了振动,叶片的前五阶振动形式主要是挥舞和摆阵振型,从第六阶开始出现了明显地扭转振动,第七、八阶振动形式复杂化,是挥舞、摆阵及扭转振动的混合振型.随着振动阶次的增高,叶片的振动形式逐渐复杂化,振动位移逐渐增大.

图6显示了叶片前四阶频率随转速的变化规律曲线.从图6中可以看出,预应力效应下旋转叶片的固有频率随转速增大而增大,这是由于叶片在旋转工况下存在动力刚化效应的缘故所造成的.与此同时,叶片的第一、三、四阶频率曲线变化幅度较大,而第二阶频率曲线变化幅度较缓慢,这表明预应力效应对叶片挥舞刚度的影响程度大于对摆阵刚度的影响.

图6 预应力效应下频率与转速的关系Fig.6 Relationship of frequency and speed under pre-stressing effect

由于转速对风电机组叶片的振动特性有较大的影响,为更加直观地分析转速对叶片振动固有频率的影响,引入模态频率偏差系数[20]来进行评价分析.其中,模态频率偏差系数由式(12)计算.

(6)

式中,fdi表示考虑转速时叶片的第i阶动模态频率；fji表示不考虑转速时叶片的第i阶静模态频率.

图7显示了风力机叶片在预应力效应下不同转速时,频率偏差系数与频率阶次之间的关系变化曲线.从图7中可以看出,叶片转速从0s-1增加到7.2s-1时,其第1阶模态频率偏差系数从-0.71%变到57.55%,第3阶模态频率偏差系数从-0.13%变到52.58%.由此可见,转速对风力机叶片的第1阶与第3阶振动频率影响较大,而对于其余各阶频率的影响程度不是很大；随转速的不断增大,叶片的各阶模态频率偏差系数也逐渐增大,这一结果说明预应力效应下高转速对叶片频率有更大的影响.

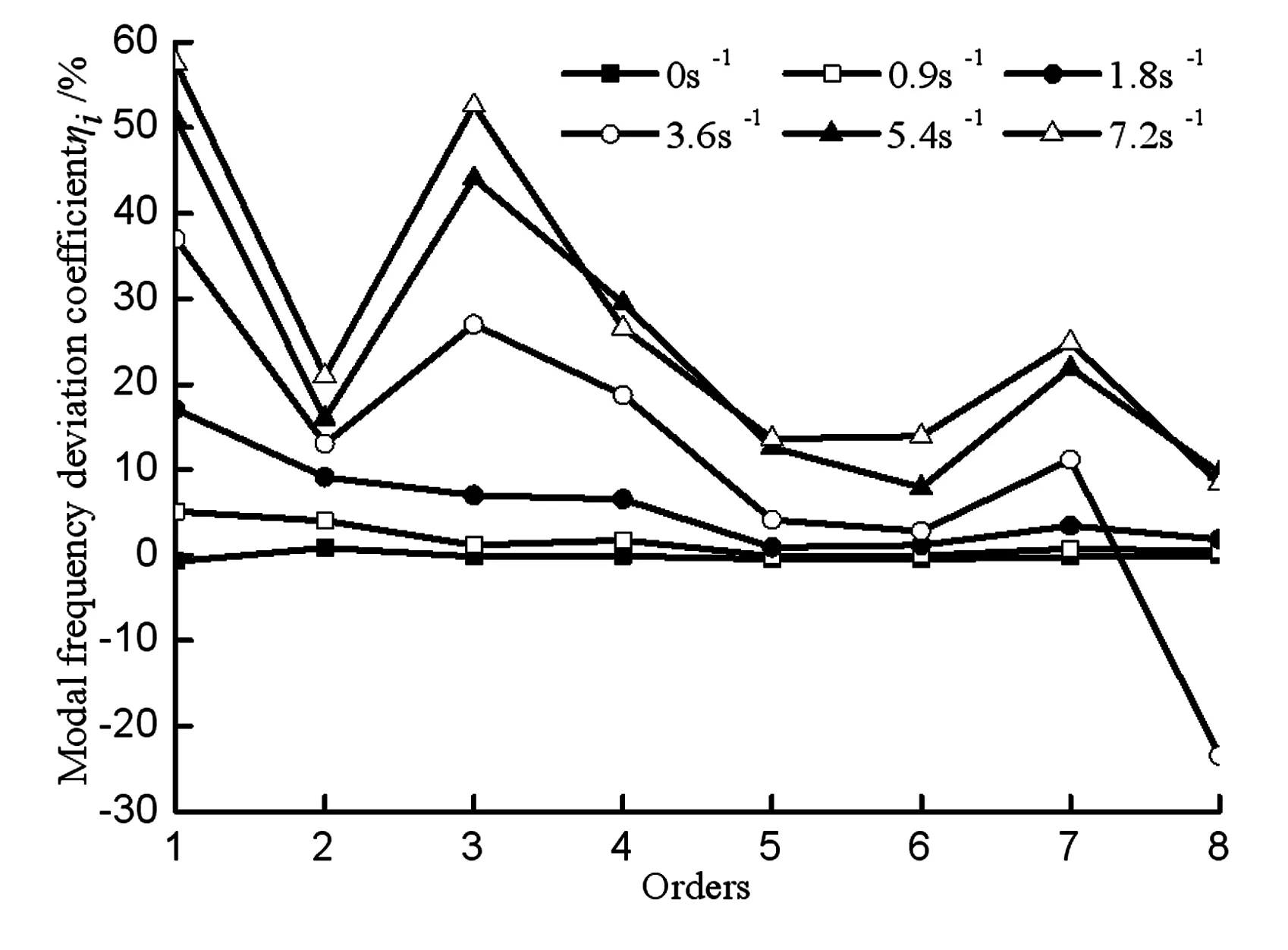
图7 不同转速下频率阶次与频率偏差系数关系Fig.7 Relationship of frequency order and deviation coefficient at different speeds

4 结论

针对风力机叶片振动特性问题,建立了风力机叶片有限元模型,利用有限元分析软件ANSYS,定量地比较分析了叶片固有振动频率对预应力效应的敏感程度及转速对频率的影响程度,并采用数值模拟方法研究了叶片绕其转轴旋转运动时的振动模态.可得出如下结论：

(1)预应力效应是叶片在空间大范围的旋转运动和弹性变形之间的相互耦合结果,叶片刚度随着旋转速度的增大而增大.转速越高,惯性力对叶片刚度的影响越大,从而叶片的固有频率增大得越快.

(2)采用分块Lanczos法对叶片进行动力学模态分析,得出叶片的前八阶固有频率和振型,结果表明挥舞和摆阵振动是叶片的主要振型,是叶片产生疲劳破坏的主要原因.

(3)空间上叶片绕其转轴做大范围的旋转运动与其弹性变形间相互耦合作用导致叶片刚度矩阵增大,产生预应力效应.随着叶轮转速的提高,预应力效应对叶片刚度的影响程度也逐渐增大,叶片的固有频率随之增大.预应力效应对挥舞刚度的影响程度大于对摆阵刚度的影响.