复合材料细长柱受冲击荷载动力屈曲研究*

汪永军 张渲铃 李映辉

(西南交通大学 力学与工程学院, 成都 610031)

引言

在对结构承受轴向冲击荷载作用的研究中,Koning和Taub[1]对两端简支,具有初始弯曲度的杆受轴向冲击荷载作用进行了研究,讨论了轴向冲击荷载小于、等于及大于静态欧拉荷载三种情况结构屈曲.Ari-Gur等[2]通过实验与理论分析,研究了轴向冲击荷载作用下金属材料柱的动力学响应,利用Rayleigh梁理论对具有初始几何缺陷柱进行建模,用有限差分法对系统求解.Hayashi和Sano[3,4]研究了低速与高速冲击下,两端铰支且初始处于弯曲状态下柱的动力屈曲问题.Ji和Waas[5]研究了轴向冲击荷载作用下细长柱的动力屈曲,文章引入了临界动力屈曲时间.

杨毅等[6]在传统解析法的基础上,推导了位移形式的传递函数矩阵,研究了圆柱壳自由振动特性.王宇等[7]基于薄壳理论,研究了薄壁圆柱壳的高阶模态振动特性.Krishnamurthy等[8]用有限元法研究了金属冲击块冲击下,复合材料圆柱壳的动力学响应及残余损伤.Her和Liang[9]采用有限元法研究了复合材料壳在轴向低速冲击下的动力学响应.Zhao和Cho[10]研究了低速冲击下复合材料壳损伤的产生与传播,用八节点非协调单元分析了层间应力及渐进失效机理.

目前,对复合材料柱在轴向冲击荷载作用下的动力屈曲问题研究较少,且在已有研究,多采用实验与数值分析相结合的方法.本文将基于单层本构关系,建立复合材料柱在轴向冲击荷载下的轴向及横向耦合振动方程,用Laplace变换求解结构轴向振动方程,得到结构轴向运动的解析解.将上述解析解代入横向振动方程,用Galerkin法求解结构横向振动方程,分析冲击过程中各参数对结构动力屈曲时间的影响.

1 轴向冲击荷载下复合材料细长柱动力学控制方程

1.1 轴向冲击荷载下复合材料细长柱动力学模型

图1为坐标系x-y-z中,轴向冲击荷载下复合材料细长柱模型,下端与基础刚性固定连接,上端为滑动铰支座.其中柱长L,截面半径R,铺层数n.第i层材料密度ρi(i=1,2, … ,n),第i厚度hi=ri-ri-1,ri为第i层半径.

1.2 轴向冲击荷载下复合材料细长柱的运动平衡方程

对轴向冲击荷载下复合材料细长柱作如下假设：(1)结构变形处于线弹性状态；(2)不考虑变形过程中截面的转动效应；(3)截面变形满足平截面假设；(4)层间位移连续.

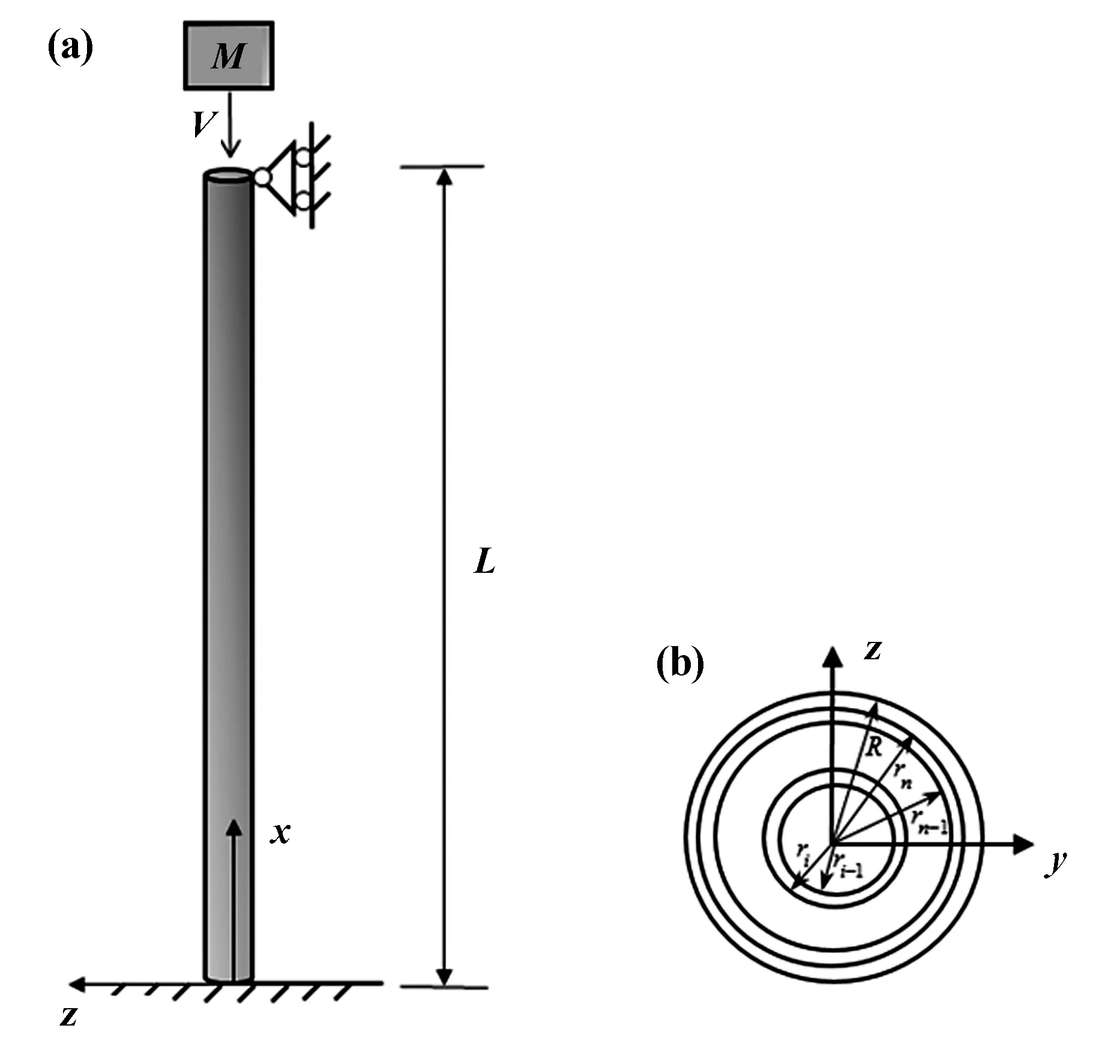
图1 复合材料细长柱及截面图Fig.1 Composite slender column and its cross section

1.2.1单层材料本构关系

图2给出了材料纤维角示意图,θ为纤维方向角,表示从x轴转向1轴的角度,以逆时针为正.其中x轴为整体坐标系方向,1方向为纤维方向.

图2 材料纤维角Fig.2 Fiber angle of material

单层材料应力-应变关系为[11]

(1)

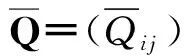
Q22sin4θ

Q12(sin4θ+cos4θ)

Q22cos4θ

2Q66)sin3θcosθ

2Q66)sinθcos3θ

Q66(sin4θ+cos4θ)

(2)

式中,Q11=E1/(1-ν12ν21),Q22=E2/(1-ν12ν21),Q12=ν21E2/(1-ν12ν21),Q66=G12.其中,E1,E2为复合材料主方向弹性模量,G12为剪切模量,ν1,ν21为泊松比.

1.2.2内力计算

由Kirchhoff基本假定,几何关系为：

ε=ε0+zK

(3)

式中,ε0=(εx0,εy0,εz0)T,εx0=u,x,εy0=v,y,γxy0=u,y+v,x；εx0,εy0及γxy0为中面应变,u,v及w分别表示层合梁中面在x,y及z方向上的位移.K=(Kx,Ky,Kxy)T,Kx=-w,xx,Ky=-wyy,Kxy=-2w,xy, 其中Kx,Ky表示中面弯曲挠曲率,Kxy表示中面扭曲率.

截面内力为：

(4)

式中N=(Nx,Ny,Nxy)T.将式(3)代入(4)得：

N=Aε0

(5)

仅考虑x-z平面内振动,有：

(6)

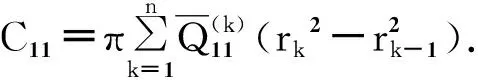
截面内力矩为：

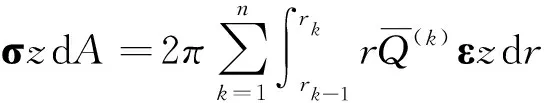
(7)

可得：

(8)

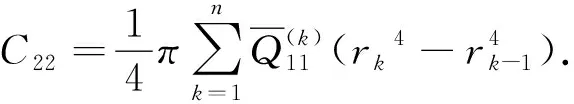
1.2.3运动方程

取微段dx作为研究对象,受力如图3.

图3 微元体受力Fig.3 Deformation of an element

由D′Alembert原理得：

(9)

(10)

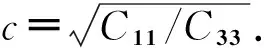
1.2.4初始及边界条件

对图1所示受冲击荷载柱轴向初始条件及边界条件为：

(11)

u(0,t)=0

(12)

其中,V为质量块与铰支端接触时的速度,M为冲击质量.

横向初始条件及边界条件为：

(13)

(14)

2 轴向冲击荷载下复合材料细长柱响应

2.1 方程求解

2.1.1轴向运动解

对式(9)进行Laplace变换,并考虑初始边界条件式(11)得：

(15)

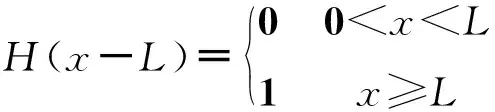
(16)

对边界条件式(12)进行Laplace变换可得：

(17)

方程(15)的通解可表示为：

U(x,s)=c1e(s/c)x+c2e-(s/c)x+

(18)

由于0≤x≤L时,其特解恒为零.将式(17)代入得：

c2=-c1

(19)

对c1进行Taylor展开得：

(20)

将式(19)～(20)代入(18)整理得：

(21)

对式(26)进行Laplace逆变换,得轴向位移解析式为：

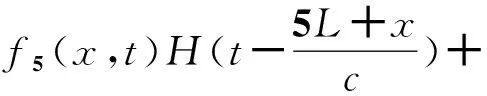
(22)

其中,fi(x,t)(i=1,2,3,…,I)为Laplace逆变换后的系数函数,其表达式见附录.

2.1.2横向运动求解

(23)

其中,κ2=C22/C11,β4=C33/C22.

设上式解为：

w*(x,t)=eiΩtW(x)

(24)

其中,i为虚数单位,Ω为固有频率.将式(24)代入(23)可得：

(25)

其中,W(x)为满足边界条件的模态函数,设：

(26)

其中,ci为待定常数,N为特征函数个数,Wi为满足边界条件的特征函数,可取为：

Wi(x)= (cosβix-coshβix)-

(27)

其中,βiL≈(4i+1)π/4.

将式(26)～(27)代入式(25),可得到残差F(x),由Galerkin法：

(28)

可得：

(K+P)c=Ω2Mc

(29)

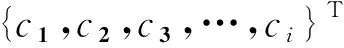
(30)

(31)

(32)

由ci(i=1,2,3,…J)不全为零得：

|K+P-Ω2M|=0

(33)

因P随时间变化,由式(33)可得Ω也随时间变化.当Ω为实数时,式(24)有界；当Ω变为复数且具有负虚部时,式(24)会随着时间的增加趋向无穷,此时动力曲屈发生.结构首次发生动力屈曲所对应的时间即为临界动力屈曲时间.

冲击块与结构的接触时间可通过式(22)确定.当冲击块与柱分离时,柱顶端(x=L)处对应的轴向边界条件为：

(34)

通过上式可得冲击块与结构的接触时间.

2.2 数值计算与讨论

本节通过数值方法,研究在不同冲击质量、冲击速度,纤维方向角对复合材料柱动力屈曲时间及冲击块与结构接触时间的影响.计算中复合材料柱模型为对称铺层,铺层数量为4,材料参数如表1,纤维方向角为θ=(-80°/80°)s,M/m0=0.1,m0为柱的质量,L=0.9m,R=0.005m,V=1.5m/s.

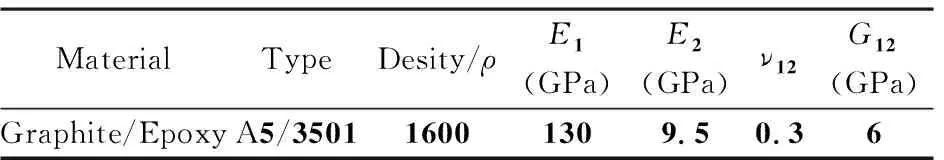
表1 材料常数Table 1 Material parameters

下述计算过程中,若未特殊说明,所选参数如上所述.

2.2.1收敛性

式(22)所取项数I和式(26)所取特征函数个数J都对精度产生影响.表2给出t*=0.0002s,J=32时,不同I对前4阶频率影响；表3给出了在t*=0.0002s,I=6时,不同J对前4阶频率影响.可见,当I=6,J=32时,各阶频率趋于稳定.下述计算章节取I=6,I=32.

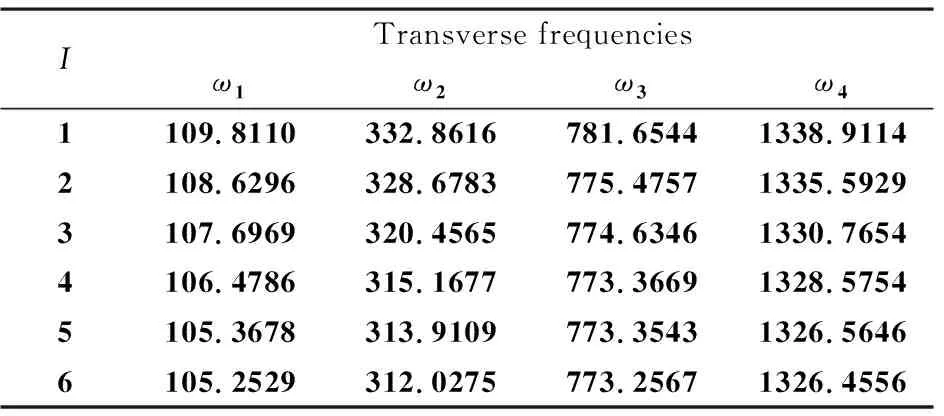
表2 横向振动频率随I变化(J=32)Table 2 Transverse frequencies with the variation of I(J=32)

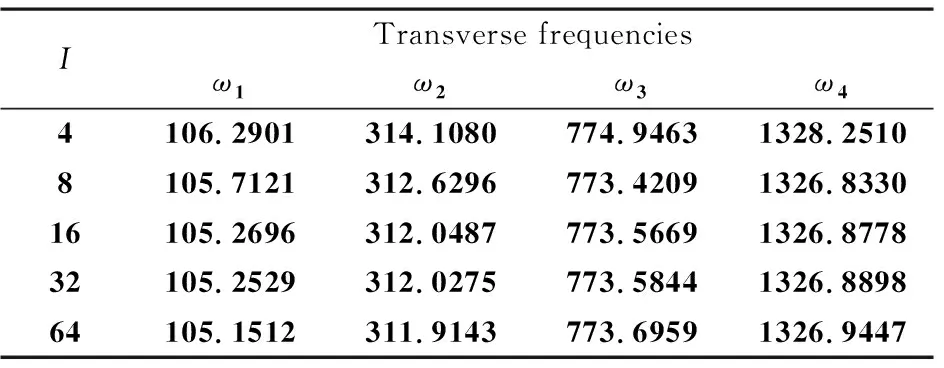
表3 横向振动频率随J变化(I=6)Table 3 Transverse frequencies with the variation of J(I=6)

2.2.2冲击质量影响

图4给出了冲击质量对动力屈曲时间与接触时间的影响.随着冲击质量增加,结构轴向冲击力增大,导致横向刚度减小,所以动力屈曲时间减小；接触时间随着冲击质量的增加而增加,两者之间呈线性关系.当冲击质量小于0.15m0时,在当前所给参数情况下,结构动态屈曲时间不存在,即结构不会出现动力屈曲.

图4 动力屈曲时间与接触时间随冲击质量变化Fig.4 Dynamic buckling time and contact duration with the variation of impact mass

2.2.3冲击速度影响

图5给出了动力屈曲时间与接触时间随冲击速度变化.当冲击速度V增加,结构轴向冲击力增大,导致横向刚度减小,所以动力屈曲时间减小；当冲击速度小于2m/s时,在当前所给参数情况下,其屈曲时间不存在,即不会出现动态屈曲,而冲击速度与接触时间无关.

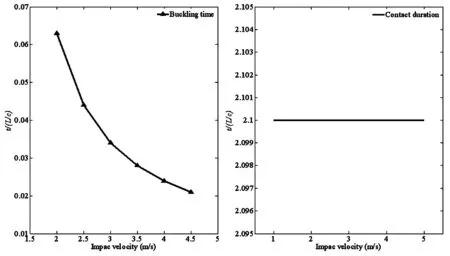
图5 动力屈曲时间与接触时间随冲击速度变化Fig.5 Dynamic buckling time and contact duration with the variation of impact velocity

2.2.4铺层角影响

图6给出了动力屈曲时间与接触时间随复合材料铺层角变化.随着铺层角度增加,结构横向刚度减小,动力屈曲时间降低；且当铺层角大于80时,结构横向刚度变化很小,所以在质量与速度一定的情况下,结构动力屈曲时间变化不大；铺层角对冲击质量块与结构接触时间无影响.

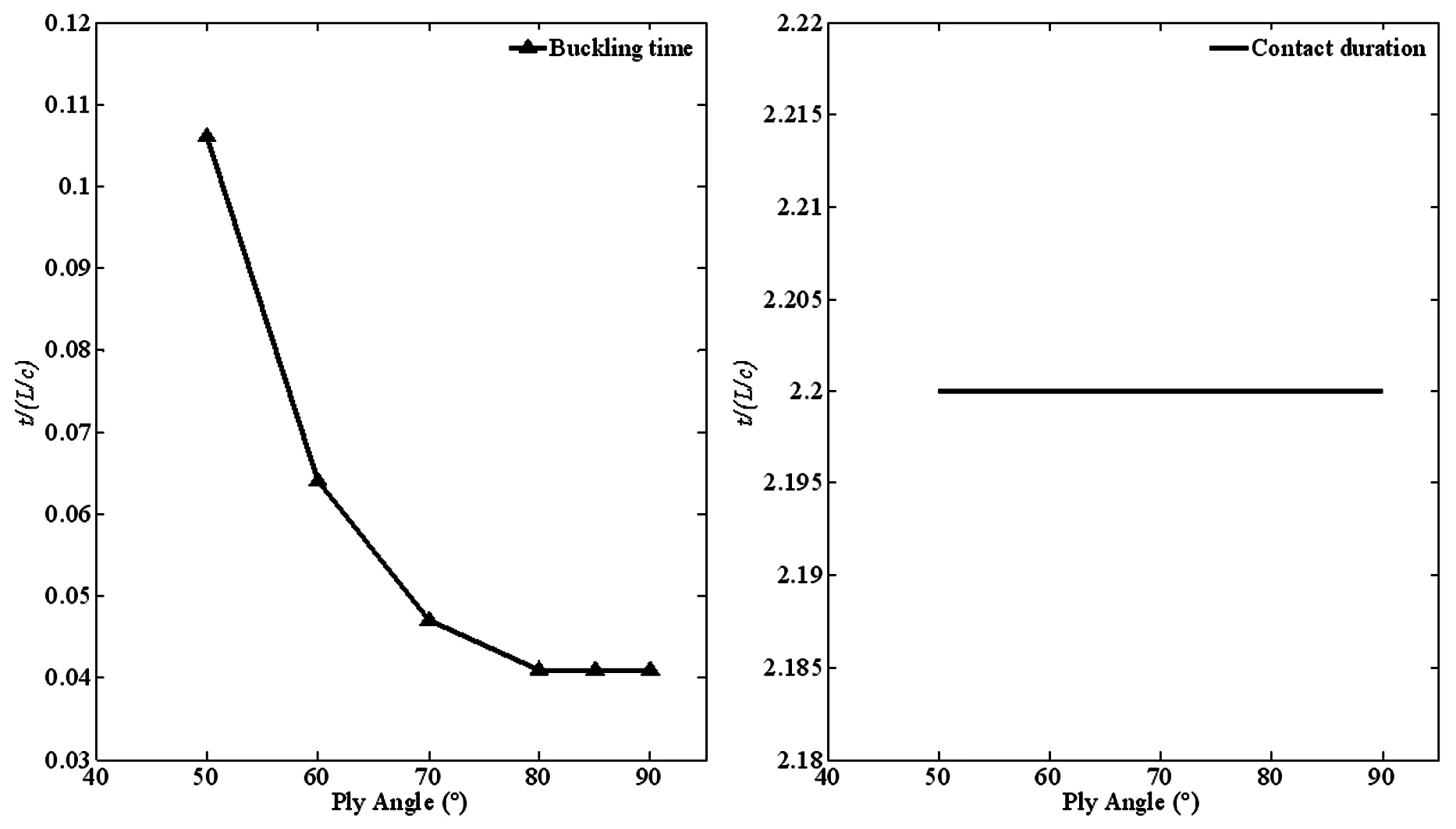
图6 动力屈曲时间与接触时间随铺层角变化Fig.6 Dynamic buckling time and contact duration with the variation of fiber angle

3 结论

研究了轴向冲击荷载作用下复合材料柱的动力屈曲特性,讨论了冲击质量、速度,纤维方向角对动力屈曲时间及冲击块与结构接触时间的影响,可得出如下结论：

(1)随着冲击质量、冲击速度,复合材料纤维方向角的增大,结构横向刚度都将减小,导致结构动力屈曲时间减小.

(2)冲击速度,铺层角对质量块与结构的接触时间无影响.

(3)增大冲击质量将增加质量块与结构接触时间,两者呈线性关系.