宽带随机激励下单自由度双边非对称碰撞振动系统的稳态响应*
王剑龙 冷小磊 刘先斌
(南京航空航天大学 机械结构力学及控制国家重点实验室, 南京 210016)
引言
由于生产误差或者制造需要,机械装置各部件间普遍存在间隙,这些间隙将导致零部件之间产生碰撞振动. 汽车、飞机、火箭、高速列车等机械系统在运行过程中会受到各种不确定载荷的作用而发生碰撞振动,对系统的动力学特性、可靠性和寿命产生重要的影响. 因此研究碰撞振动系统在随机载荷下的响应,具有重要的工程实际意义.
半个世纪以来,国内外学者对碰撞振动进行了广泛的研究.目前,国内外关于该领域的研究主要集中在用现代分析方法研究在确定性激励作用下碰撞系统的响应和稳定性.谢建华[1,2],丁旺才[3,4]等基于Poincaré映射研究了确定性载荷作用下的碰撞振动系统的对称性,分岔及混沌.对于随机载荷下的碰撞振动系统的响应的研究还相对较少.Dimentberg[5]用随机平均法研究了高斯白噪声激励下单自由度碰撞振动系统的随机响应. 黄志龙[6]等发展了适用于强非线性系统的随机平均法,研究了宽带随机激励下单自由度碰撞振动系统的随机响应.吴禹[7]通过摄动法求解泊松白噪声激励下多自由度碰撞振动系统的FPK方程,得到系统的近似平稳响应.以上几位学者所用的碰撞模型主要是弹性碰撞模型,对于刚性碰撞模型,杨贵东[8]等基于等效非线性系统方法和突变理论,分析了随机参激下Duffing-Rayleigh碰撞振动系统的P-分岔.李超[9]通过非光滑变换把原系统化为新的系统,应用能量包线随机平均法分析了相关高斯白噪声激励下的Duffing-Van der Pol碰撞振子的稳态响应,并分析了不同参数下发生的随机分岔.迄今,对于采用弹性阻尼碰撞模型双边非对称约束的碰撞振动系统随机响应,目前可见的文献还鲜有报道.
本文采用广义Hertz接触碰撞模型,基于广义谐和函数的随机平均法研究了在宽带随机外激励下双边非对称约束的单自由度碰撞振动系统的稳态响应.此外,将广义胞映射法应用到此类碰撞振动系统,得到系统的近似稳态响应.最后用蒙特卡罗模拟验证上述两种方法的有效性.
1 动力学模型
将含间隙的复杂碰撞振动系统简化为如图1所示的动力学模型.简化为由刚度系数为k的线性弹簧和阻尼系数为c的黏性阻尼器连接而成的集中质量块m,在宽带随机激励f的作用下发生振动.
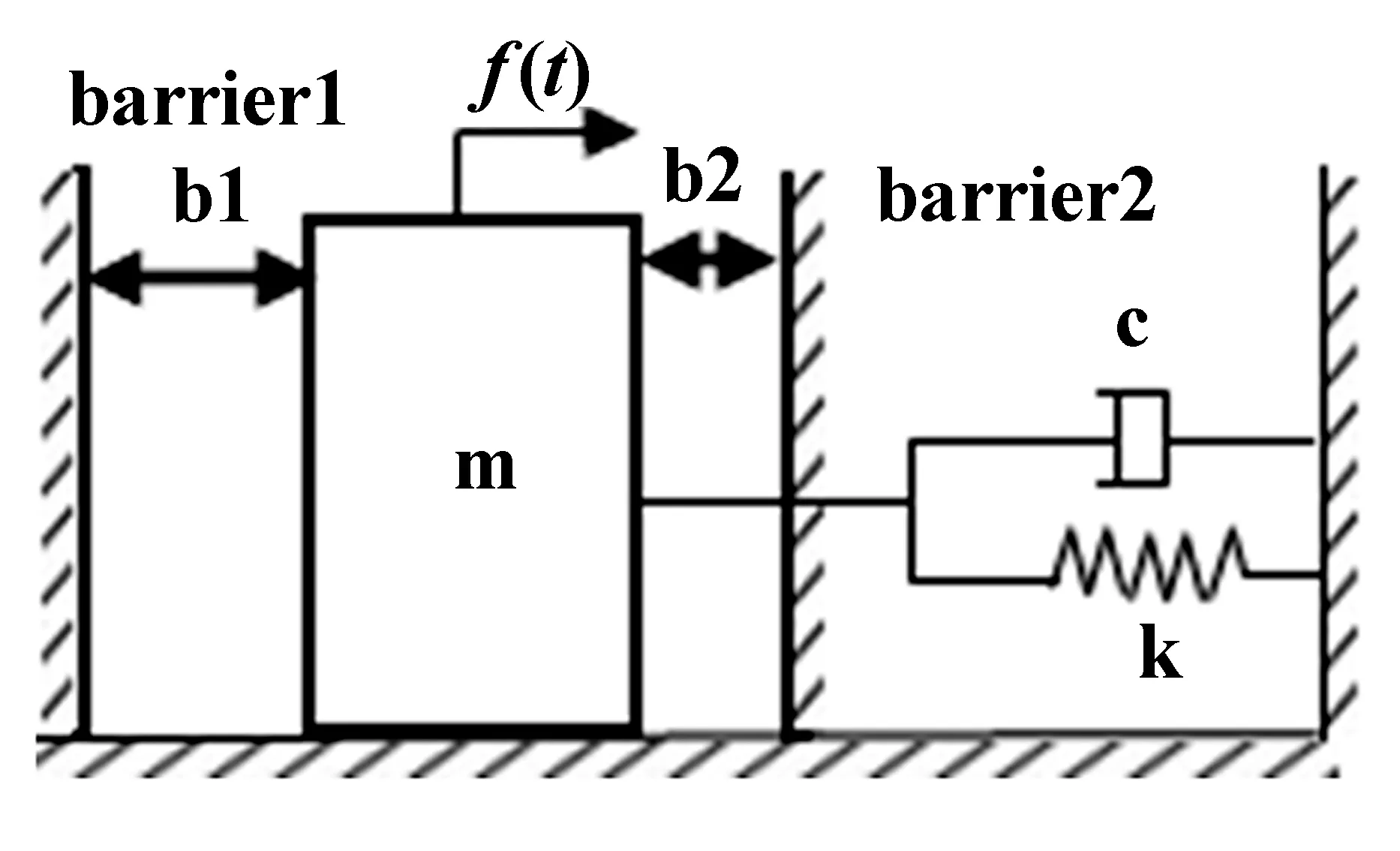
图1 碰撞振动模型Fig.1 Vibro-impact model
当振动的位移x大于间隙b2或小于间隙-b1时,质量块分别与左右两侧的挡板发生碰撞.假设碰撞满足Hertz接触条件,碰撞作用力用广义Hertz接触力用F来表示.因此系统的运动微分方程可以表示为:
(1)
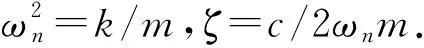
广义Hertz接触力具有如下的形式[10]:
(2)

(3)
式中:Ei和νi分别是两个质体的弹性模量和泊松比.
(4)
因而将广义Hertz接触力(2)写成:
(5)
考虑图1所示的碰撞振子,广义Hertz接触力具体表达式为:
(6)
由于广义Hertz接触力同时包含阻尼与弹性效应,因而将碰撞接触力等效分解为阻尼力和恢复力两部分,并分别与碰撞振子的线性阻尼力与弹性恢复力合并,将系统运动微分方程(1)改写为:
(7)
式中:
(8)
为系统的恢复力,
(9)
为系统的阻尼力.
2 平均法求解系统稳态响应的概率密度
方程(7)所表示的是一个强非线性系统,当系统的阻尼与随机激励的强度较小时,系统的运动是近似周期的,因而引入广义谐和变换:

(10)
其中:
Φ(t)=ψ(t)+θ(t)

(11)
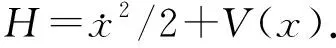
将(10)式代入到(7)式可得:
(12)
式中:
(13)
根据Stratonovich-Khasminskii极限定理[11],A和θ弱收敛于二维扩散过程,可用如下伊藤随机微分方程描述:
(14)
其中重复下标表示求和,Br(t)表示相互独立的单位维纳过程,漂移系数和扩散系数为:
(15)
而Rf是随机外激励的自相关函数.
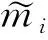
(16)
式中:
(17)
在实际计算时,可将v、mi、σi关于Φ展开成傅里叶级数,取其前几项代入式(15),并完成确定性平均,得到伊藤微分方程的漂移与扩散系数的具体表达式.
由方程(16)中第一式不依赖于θ可以看出,幅值A本身就是一个齐次的扩散过程,其转移概率密度p(A,t|A0)由如下FPK方程控制:
(18)
其初始条件为p(A,t|A0)=δ(A-A0),t=0.
由方程(18)可得幅值A的稳态概率密度为:
(19)
式中C为归一化常数.系统总能量H的稳态概率密度为:
(20)
这里的A=V-1(H是H=V(A+B(A))的反函数.系统的位移与速度的联合稳态概率密度为:
(21)
系统位移稳态概率密度为:

(22)
3 广义胞映射法
考虑到系统所受的激励为宽带噪声,根据文献[11],如果激励的相关时间足够小,系统的响应将是近似的马尔科夫过程,此时可以应用广义胞映射法高效地计算响应的稳态概率密度.在计算广义胞映射一步转移概率密度矩阵时,我们选取的一步转移时间要远大于系统激励的相关时间,这样系统每一步的响应增量可看成是近似独立的,即满足马尔可夫假设.
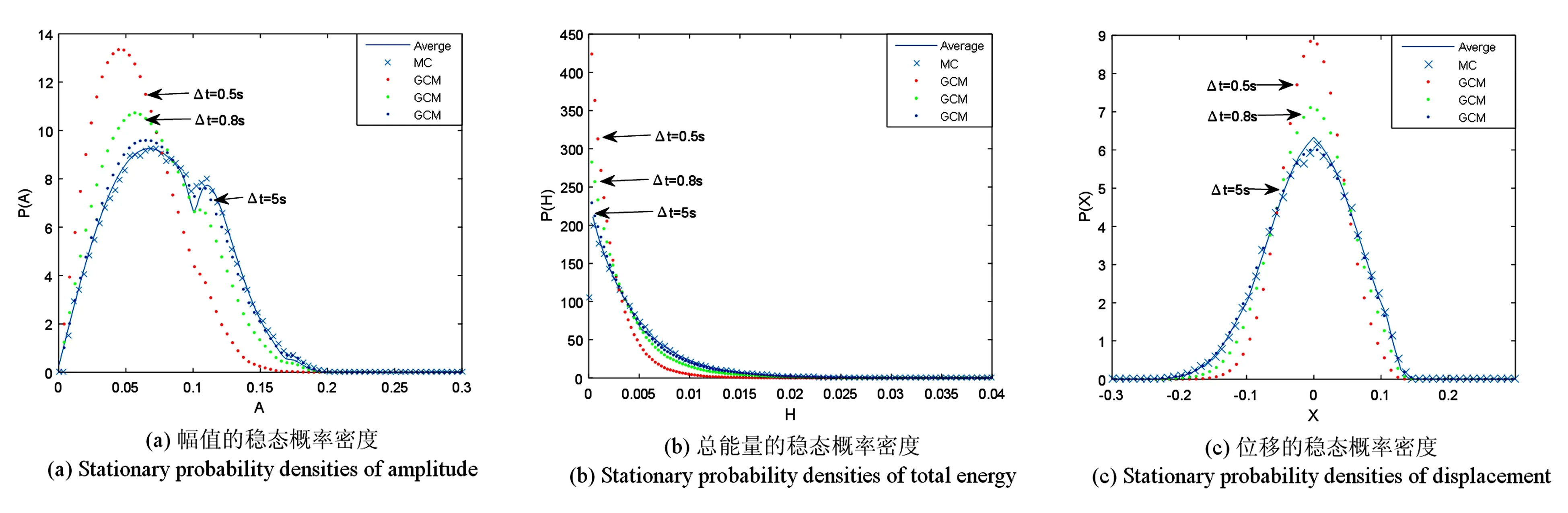
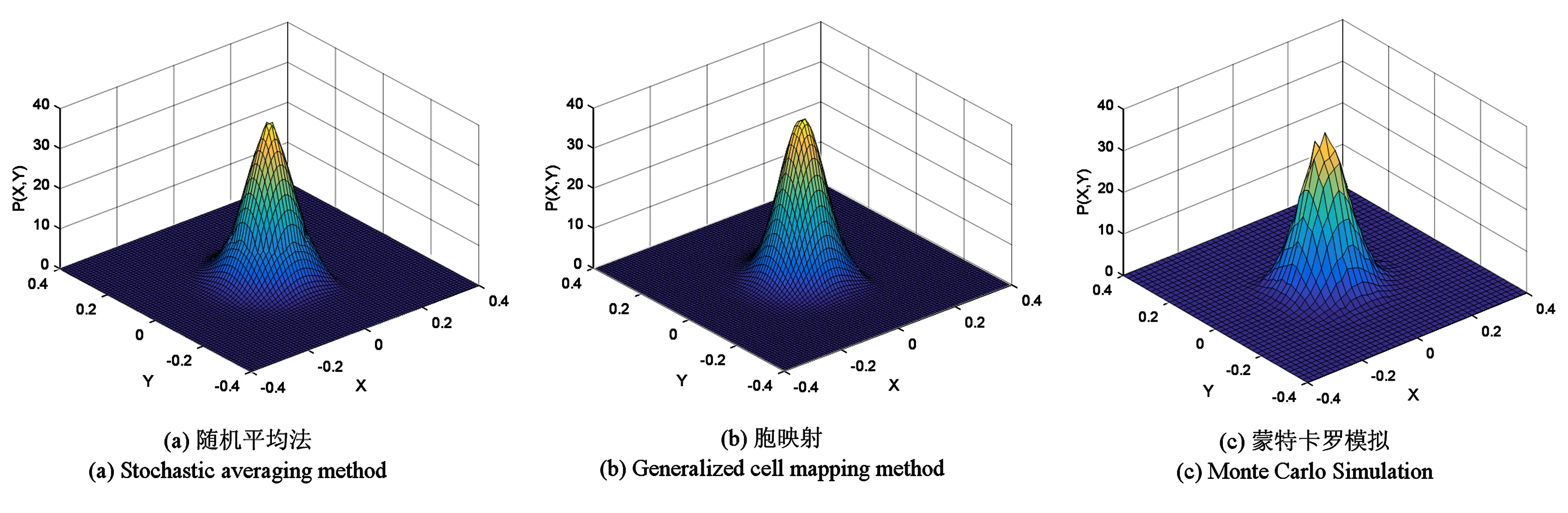
在算例中,广义胞映射计算系统稳态概率密度的实际步骤如下:首先,选择感兴趣的如下区域Z={-0.4 p(n)=P·p(n-1)=Pn·p(0) 经过多次迭代得到系统的稳态响应. 在图1所示系统中,考虑系统所受随机外激励f(t)的功率谱如下: (23) 其中ζ1,ω1,D为常数,该噪声可由噪声强度为2D的白噪声经过一个二阶滤波器生成,噪声的带宽取决于参数ζ1,ω1. 选取系统参数:m=1,ζ=0.1,ωn=1,kc=80,α1=0.1,b1=0.2,b2=0.1,ζ1=0.6,ω1=6,D=1.2. 分别按照随机平均法和广义胞映射法计算系统幅值、总能量、位移的稳态概率密度及位移和速度的联合稳态概率密度.图2(a)、(b)、(c)分别给出了上述参数下系统幅值、总能量和位移稳态概率密度,—线表示平均法的结果,•线表示胞映射结果,×表示蒙特卡罗模拟结果.图3给出了系统位移和速度的联合稳态概率密度.从图2可以看出随机平均法的结果与蒙特卡罗模拟的结果吻合的很好,证实了上述推导的随机平均法的有效性.此外可以看出,随着广义胞映射法的一步转移时间的增长,广义胞映射法所得结果的精确性得到很大的提高,说明对于宽带激励下的系统,应用适当的广义胞映射法也可以得到足够精确的稳态解. 取另一组噪声参数ζ1=0.3,ω1=5,计算系统在不同噪声强度D=0.4、0.8、1.2下幅值的稳态概率密度.从图4(a)可以看到随着噪声强度的增强,系统的非线性效应增强,幅值的稳态概率密度发生较大的变化,概率分布总体向右移.当噪声强度为D=0.4时,幅值概率分布主要集中在0到0.1之间,系统的振子主要在平衡位置附近来回震荡,不与两侧的碰撞壁发生碰撞.随着噪声强度增强到D=0.8,有较大一部分幅值稳态概率落在了幅值0.1到0.1685之间,系统运动过程中发生单边碰撞的概率增大,即振子在运动一个来回过程中与较近侧的碰撞壁b2发生碰撞而不与远处碰撞壁b1碰撞的概率增大.噪声强度继续增强,到D=1.2时,系统运动发生单侧碰撞的可能性继续增大,出现双侧碰撞的可能性也有明显的增加. 图2 幅值、总能量及位移的稳态概率密度Fig.2 Stationary probability densities of amplitude, total energy, displacement 图3 位移与速度的联合稳态概率密度Fig.3 Joint probability density of velocity and displacement 图4 幅值、总能量及位移的稳态概率密度Fig.4 Stationary probability densities of amplitude, total energy, displacement 采用广义Hertz接触模型,将碰撞振动系统的碰撞特性等效为非线性弹簧-阻尼器,建立了一类双边非对称约束的碰撞振动动力学模型.这种碰撞模型兼具刚性碰撞模型和Hertz接触模型的优点,比较符合实际的碰撞过程.利用基于广义谐和函数的随机平均法研究系统的稳态响应,并用蒙特卡罗模拟验证了该方法的有效性.对于这类强非线性碰撞振动系统,通常的线性化处理方法不再适用,而用该随机平均法仍可得到很好的结果.并且,由本文算例可见,随着激励强度的增强,碰撞系统的非线性效应增强,幅值的稳态概率密度出现较大的变化.此外,利用广义胞映射法得到系统的稳态响应,说明当系统的噪声激励为非白的时,如果广义胞映射的一步转移时长取的足够大,远大于噪声各分量的相关时间,利用广义胞映射方法也可以得到很好的结果.4 算例

5 结论

