移动车辆桥梁系统中的振动能量获取*

朱培 任兴民 秦卫阳 杨永锋 王元生 周志勇

(西北工业大学力学与土木建筑学院,西安 710072)

引言

车辆驶过桥梁时会引起桥梁的振动,这种振动有时很剧烈,可以将这种振动能量转化为电能,为一些传感器设备供电,这具有很重要的实际价值与意义,国内外已经开展了相关的探索性研究.Ju[1]建立了半车模型,采用有限元法分析其变速通过桥梁时系统的动力响应.彭献[2-3]研究了动质量模型加速或减速通过简支梁时对桥梁跨中挠度的影响.Raske[4]和Fryba[5]对移动荷载作用下各向同性板的动态响应进行了很好的研究,并且得到了经典的解决方案.Miha[6]研究了四边简支板在动质量块作用下的振动响应,并把质量块的荷载分布形式分简化为集中载荷、均布载荷和线性分布载荷,研究发现质量块移动速度、荷载分布形式和质量块的质量大小对板的振动响应影响较大.

压电类材料具有很高的能量密度,利用压电装置可产生较大功率的电能.随着物联网及微机电的发展,压电发电受到人们更多的关注,很多学者在压电俘能方面进行了研究[7-15],这将会使得越来越多的压电产品得以广泛应用.Han[16]对移动荷载作用下变截面梁的电磁式能量获取进行了分析,研究发现荷载的移动速度对俘能效率有较大影响,并对电磁式能量采集装置中的参数进行了优化.Green等[17]研究了在人体运动和桥梁振动激励下的能量获取,其激励源是根据统计资料分析得到的.Ali[18]等研究了移动点荷载通过二维梁模型时的动力响应,并以此作为激励研究了压电能量的获取.Kim[19]等以欧拉伯努利梁作为桥梁模型并将压电片附着在桥梁表面,研究了可变荷载通过桥梁时压电片获取的能量.实验结果和数值结果表明移动荷载的速度及大小对桥梁应变影响较大并且俘获的能量随着应变的增大而增大.Gatti等[20]研究了火车轨道轨枕的压电能量获取,通过测量得到火车轨枕的振动加速度,并将其作为振源激励对压电俘能装置进行了数值模拟和理论分析,研究发现电量输出与加速度幅值的平方成正比.Karmi等[21]研究桥梁振动的压电能量获取,通过将车辆简化为质量块和将桥梁简化为简支梁,研究了车速、俘能装置阻抗对能量输出的影响.

本文研究了车辆—桥梁系统中压电俘能装置的俘能特性.将车辆简化为移动车轮—弹簧—阻尼器—簧上车身质量模型,又将桥梁系统简化为对边简支对边自由板并建立了广义坐标下的车辆—桥梁系统运动微分方程.再以桥梁激励作为振源建立了压电俘能器压电动力学耦合微分方程,研究了车速、车身质量、压电装置位置、压电梁厚度对俘能特性的影响.

1 车辆动力作用下桥梁模型

车辆动力作用下的桥梁模型如图1所示,桥梁模型简化为均质材料的各向同性矩形薄板,x向长度为a,y向长度为b.车辆模型简化为车轮—弹簧—阻尼器—簧上车身质量体系,其中车轮质量为mw,弹簧刚度kv,阻尼为cv,簧上车身质量为mv,并以速度v沿x方向行进,偏离x轴的距离为e.EH为压电俘能器,内部采用结构简单性能较好的带末端质量块的压电悬臂梁结构,如图2所示.

图1 车辆动力作用下的桥梁模型图Fig.1 Bridge model with moving vehicle

图2 悬臂梁压电俘能器EH内部结构Fig.2 Internal structure for cantilever-beam piezoelectric energy harvester EH

移动荷载作用下各向同性矩形薄板的运动微分方程为：

(1)

其中：

(2)

(3)

式中(vt,e)表示车辆位置坐标;ρ,h,c分别为矩形薄板的密度,厚度和阻尼系数;fc(x,y,t)为车轮与板之间的接触力;w(x,y,t)为板在坐标(x,y)处t时刻的挠度;用δ函数描述车辆的位置且表示如下:

(4)

假定车辆模型通过桥梁时,车轮与板不发生分离,即车轮的竖向位移与其所在处板的挠度相同,即有：

w(x,y,t)|x=vt,y=e=zw(t)

(5)

其中zw(t)为车轮处的位移.

令车身在竖直方向的位移为z(t),其运动微分方程可表示如下：

(6)

车轮与板之间的接触力可表示为：

(7)

根据以上分析,采用模态叠加法,板的挠度可表示为如下形式：

(8)

式中Wmn(x,y)为对质量归一化的第(m,n)阶振型函数,Tmn(t)为相应的模态坐标函数.将式(8)代入式(1),并在方程两端同时乘Wηε(x,y),再对x从零到a积分,对y从零到b积分,假设阻尼在模态变换中可对角化,可得:

k(z(t)-w(vt,e,t))+mwg)

(9)

其中：

(10)

(11)

(12)

可将式(9)表示为如下矩形形式：

(13)

(14)

(15)

(16)

C(t)=Cd+Cu

(17)

其中：

Cd=

(18)

(19)

K(t)=Kd+Ku

(20)

(21)

(22)

(23)

(24)

(25)

(26)

因此车身的运动微分方程可进一步表示为：

(27)

上式可写为如下矩阵形式：

(28)

联立式(13)和式(28)可得车辆与矩形薄板的耦合运动方程：

(29)

桥梁模型可简化为对边简支对边自由矩形薄板,若平行于x轴两边为自由边,平行于y轴方向为固支边,则相应振型边界条件满足[18]：

(30)

(31)

板的第(m,n)阶固有频率ωmn可由下式得到：

sinβ1mnbshβ2mnb

=0

(32)

相应的振型函数为：

Wmn(x,y)=

(33)

式中：

(34)

β1m,β2m为满足振动微分方程的特征方程的特征根：

(35)

(36)

2 悬臂梁压电振子基本结构

目前应用比较普遍的压电俘能装置主要采用悬臂梁压电振子结构,如图2所示.这种俘能装置主要由压电晶体材料、负载阻抗、弹性基体材料和质量块组成.质量块M固定在悬臂梁的自由端,通过调节质量块质量大小可调节压电振子的共振频率大小.在车辆荷载作用下桥梁产生的位移激励引起悬臂梁压电振子振动,通过压电效应可实现振动能向电能的转化.根据欧拉伯努利梁振动理论和基尔霍夫第一定律可得压电俘能系统的耦合运动方程:

(37)

(38)

式中EI是压电梁的弯曲刚度,wb是基础横向位移,wrel是压电梁相对于基础的横向位移,mps为压电梁单位长度的质量,L是金属基层长度,Cs为内粘性阻尼,Ca是外部介质的粘性阻尼,V(t)是压电电压,ϑ是机电耦合系数,RL为电路阻抗,C为电路电容.弯曲刚度可表示为：

(39)

压电梁单位长度质量可表示为：

mps=bp(ρshs+2ρphp)

(40)

其中hs为金属基层高度,hp为压电层高度,Es为金属基层弹性模量,Ep为压电层弹性模量.

压电梁相对于基础的位移响应可用如下级数形式表示：

(41)

式中φr为压电梁的第r阶模态函数,η为相应的模态坐标.将式(41)代入式(37)和式(38)中,应用模态函数正交性可得模态坐标下的压电梁运动方程：

(42)

(43)

其中ωr为压电梁的第r阶振动频率,ζr为相对应的模态阻尼,a(t)为基础激励加速度.

(44)

(45)

v=-e31bhpc

(46)

其中b为压电层宽度,e31为压电常数,ε33为介电常数,hpc为压电层到金属基层中性轴的距离.

3 数值算例分析

板的参数如下：板的长度a=24 m,宽度b=8 m,板厚h=0.5 m,弹性模量E=50 GPa,密度ρ=2400 kg/m3,泊松比μ=0.3,车轮质量mw=0,车身质量mv=1200 kg,阻尼系数ζ=0.03.悬臂梁参数如下长度L=55 mm,宽度bs=6.2 mm,厚度hs=0.1 mm,密度ρs=1300 kg/m3,弹性模量Es=2.4 GPa,阻尼系数ζs=0.01.压电材料参数如下：长度Lp=55 mm,宽度bp=3.8 mm,厚度hp=0.25 mm,密度ρp=7000 kg/m3,末端质量块质量M=10 g,阻抗RL=1 M,介电常数ε33=1.06×10-10F/m,压电常数e31=-23×10-10C/N.

本文选取压电梁的前5阶频率进行求解,图3为压电梁前5阶模态.

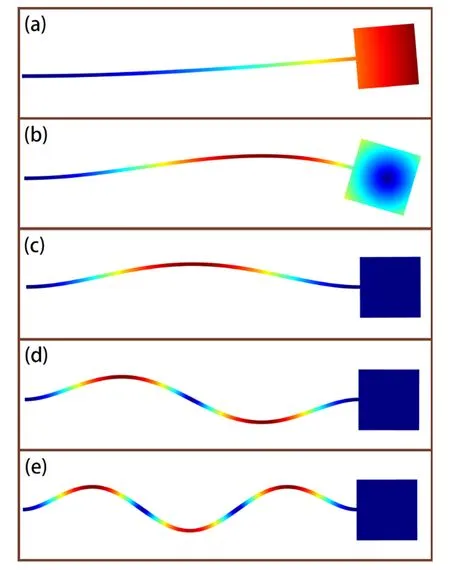
图3 压电梁1 - 5阶模态(a) 1阶0.83 Hz, (b) 2阶11.74 Hz, (c) 3阶148.63 Hz, (d) 4阶407.59 Hz, (e) 5阶797.87 HzFig.3 The first-fifth order modes of piezoelectric beam(a) first order 0.83 Hz,(b) second order 11.74 Hz,(c) third order 148.63 Hz,(d) fourth order 407.59 Hz,(e) fifth order 797.87 Hz

图4为不同车速下桥梁挠度与车辆位置关系曲线.vt/a表示车辆行驶的距离与桥梁跨度之比.当vt/a小于1时表示质量未离开桥梁,vt/a大于1表示车辆已经离开桥面,此时对应于桥梁的自由振动,为了全面的分析桥梁的振动全过程选取vt/a.从图中可以看出,当车辆以不同速度经过桥梁时,随着车速的增加,桥梁的最大挠度先变大后变小,由此可知车辆过桥时存在一临界速度使得桥梁产生的挠度最大.当车速相同时,桥梁跨中处的挠度最大,离跨中位置越远挠度越小.

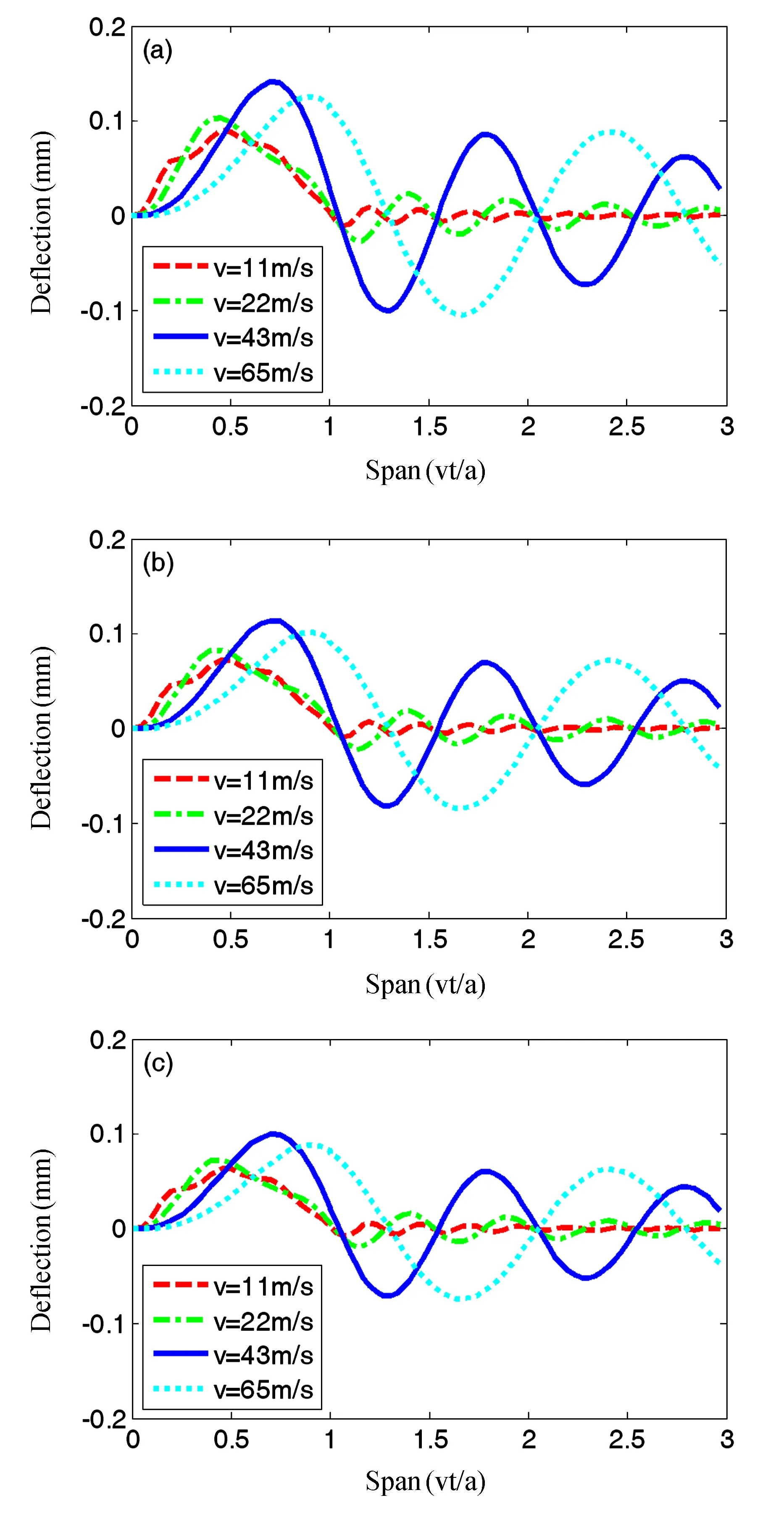
图4 不同车速下桥梁挠度与车辆位置关系曲线(a) EH在1/2跨度处, (b) EH在1/3跨度处, (c) EH在1/4跨度处Fig.4 Bridge displacement versus vehicle position curves for different moving speeds(a) EH at 1/2 span, (b) EH at 1/3 span, (c) EH at 1/4 span

从图5可以看出,电压输出的大小随着车速先增加后减小,而且当压电俘能器分布在1/2处跨度时可获取较大的电压,这与桥梁挠度值有相同的规律.这是由于当桥梁位移较大时,产生较大的振动能,压电俘能器可输出较大的电压值.

图6为车辆以不同速度经过桥梁时桥梁跨中挠度幅频曲线.从图中可知可以清晰的看出车速在43m/s时桥梁拥有最大挠度幅值,当偏离这一速度越远,挠度幅值越小.

图5 不同车速下输出电压与车辆位置曲线(a) EH在1/2跨度处, (b) EH在1/3跨度处, (c) EH在1/4跨度处Fig.5 Voltage versus vehicle position for different moving speeds(a) EH at 1/2 span, (b) EH at 1/3 span, (c) EH at 1/4 span

图6 不同车辆速度时桥梁跨中挠度幅频曲线Fig.6 Deflection-frequency curves in the middle of bridge for different moving speeds

图7为车辆以不同速度经过桥梁时,桥梁跨中的压电电压幅频曲线.从图中可以看出,电压幅频曲线与桥梁挠度幅频曲线有着相同的规律,即在车速为43m/s时压电俘能器拥有较大电压输出幅值.因此,可以看出随着桥梁挠度幅值的不断增加,压电俘能器获取的能量也不断增加,因此电压幅值也随之增大.

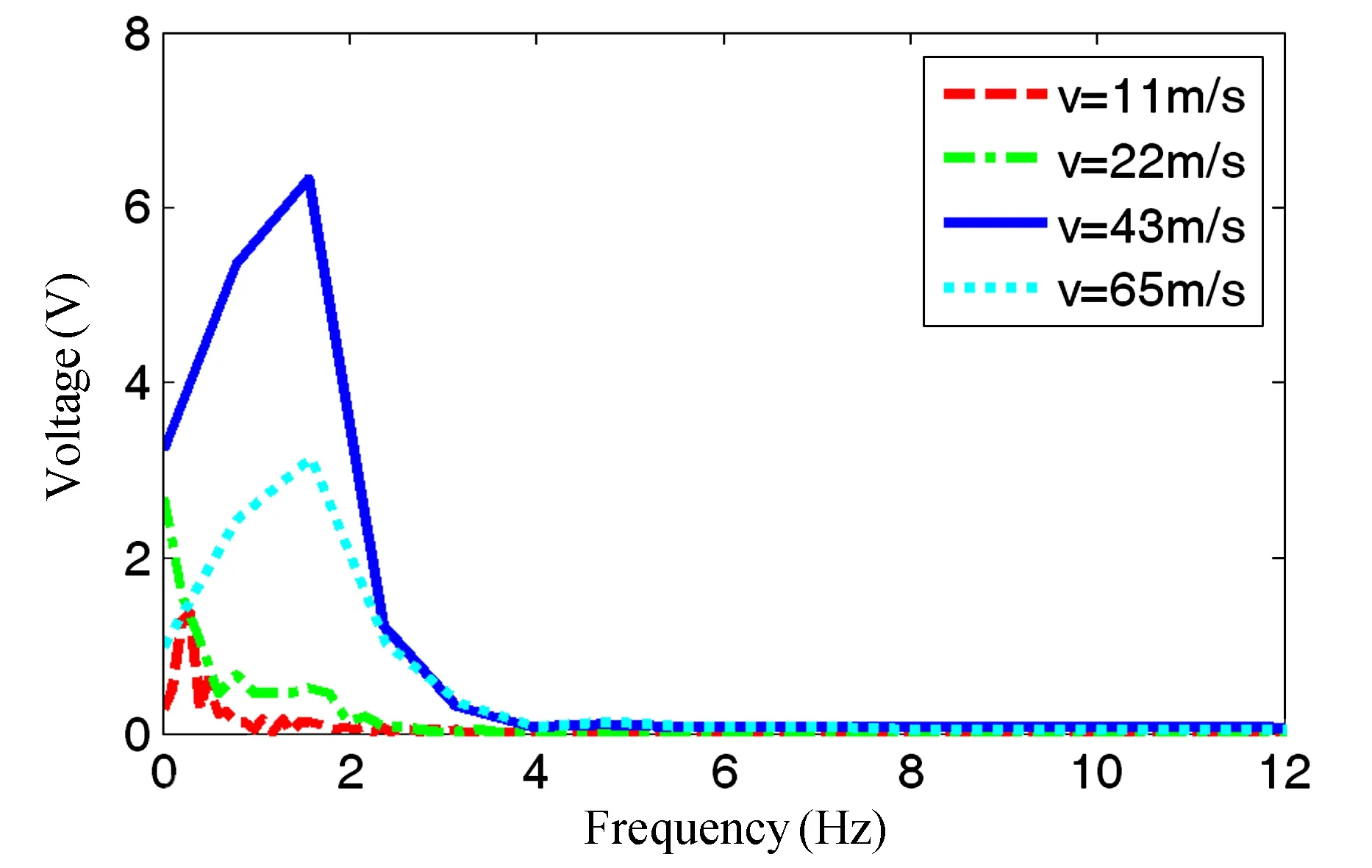
图7 车辆不同速度时桥梁跨中电压幅频曲线Fig.7 Voltage-frequency curves in the middle of bridge for different moving speeds

图8 压电俘能器分布在桥梁不同位置时车辆速度与输出能量曲线Fig.8 Energy versus vehicle speed curves for EH distributed at different positions of bridge

图9为不同车身质量时车速与输出能量曲线.从图中可以看出车身质量越大输出的能量也就越大,并且在临界车速附近时获取的能量最大.

图9 不同车身质量下车速与输出能量曲线Fig.9 Energy versus vehicle speed curves for different mass of vehicle

图10为当压电俘能器末端质量块质量不同时车辆位置与输出电压曲线.由计算可知,当质量块的质量分别为18 g,4 g,1 g,0.1 g时,压电俘能器的一阶频率分别为0.65 Hz,1.01 Hz,1.93 Hz,2.96 Hz.当质量块质量为1 g时,电压输出值最大.因此可以通过调整质量块大小使得电压输出最大化.

图10 不同质量块时车辆位置与输出电压曲线Fig.10 Vehicle position versus voltage curves for different mass of energy harvester

图11 不同梁厚度时车辆位置与电压关系图Fig.11 Vehicle position versus voltage curves for different value of cantilever beam

图11为不同梁厚度时车辆位置与电压关系图.从图中可知,在车辆行驶至3/4桥梁跨度附近时,电压输出达到最大值.并且随着梁厚度的增加,系统输出电压值是先增大后减小.当梁的厚度增加到0.4 mm时,压电输出达到最大值.因此可以通过调整压电梁的厚度对压电俘能器进行优化,从而提高电压输出的大小.

4 结论

本文通过建立单车过桥系统动力模型,分析了桥梁的振动响应,并以桥梁振动响应作为振源研究了压电俘能装置的俘能特性.研究发现车速、车身质量、压电俘能装置位置等参数对压电俘能特性的影响并得出了以下主要结论：

(1)车辆过桥梁时,存在一临界速度使得桥梁挠度最大,车速偏离临界速度越远,桥梁振动响应越小.

(2)压电俘能器分布在跨中位置时,压电俘能装置的电压输出值最大,偏离跨中位置越远,其俘获到的能量越小.

(3)车辆经过桥梁时引起的振动为低频振动,宜采用基础频率较低的结构.

(4)随着车身质量的增加,压电俘能器俘获的能量也随之增加.

(5)通过调整压电俘能装置中的末端质量块质量和压电梁厚度进行优化设计从而实现电能输出最大化.