基于智能诊断系统的精准反思*——以“分段函数”反思为例

●

(凤鸣高级中学,浙江 桐乡 314500)

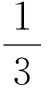
二十世纪六十年代，美国学者林斯利基于斯金纳的行为主义学习理论提出了一种教学方法，叫精准教学.他通过设计测量过程以追踪学生的学习表现，同时支持数据决策.林斯利在具体的实施过程中，又强调系统教育的评估和错误订正[3]，后来精准教学发展为可对任意指定的教学方法是否有效进行评估的一种框架.

受精准教学启发，基于记录学生学习表现的统计数据，可更精准地确定行为和评价，同时也可更精准地进行错误订正，故可借助智能诊断系统的精准分析促进学生进行精准反思.

1 “互联网+”智能诊断系统为精准反思提供了载体

本研究借助由某计算机公司开发的智能诊断系统，该系统的设计原理是：基于不同学习者知识结构以及学习水平和能力等的不同，通过知识点“合并门槛”的设置，在学习者的学习能力范围，将有关联的知识点合并为一个学习内容，使得系统自适应生成个性化的学习者学习诊断图.该系统的核心技术是将某一个数学内容分解成若干个相互有关联的知识节点，并据此设计出相应的数学测试题.这一工作是由该公司聘请的有着丰富数学教学经验的教师团队完成.

学生只要通过互联网上机，完成某个数学知识点的一些测试题，就会马上得到该生在这一学习内容上的学习诊断图，并揭示该生所犯的错误类型及原因.在此基础上还会给出相应的补救措施和途径.因此，学生可以根据这些个性化的诊断信息进行精准反思与决策.下面以“分段函数”为例进行说明.

2 基于智能诊断系统的精准反思实施过程

2.1 智能诊断系统下的精准诊断原理

人教A版普通高中课程标准实验教科书《数学(必修1)》第1.2.2节“函数的表示法”中的分段函数，是学生进入高中后遇到的第一个不同于初中所学的函数形式.它涉及函数的三要素与性质，综合性强，又是高考的热门知识点，可以很好地检验和评估学生学习后的效果.智能诊断系统将“分段函数”分解成了16个子知识节点:

1)知道分段函数;

2)会求分段函数的最值和值域;

3)会判断分段函数的单调性;

4)会求分段函数的零点;

5)会解含参的分段函数问题;

6)会建立以几何为背景分段函数关系式;

7)会解决纳税问题;

8)会建立以其他实际为背景的分段函数关系式;

9)知道取整符号含义;

10)知道含取整符号的恒等式;

11)知道含取整符号的不等式;

12)会研究取整函数的图像与性质;

13)会运用取整符号建立函数关系式;

14)能解决有关取整函数问题;

15)理解新定义sgn;

16)理解新定义min,max.

测试题围绕这16个子知识点进行设计，采用了“递归思想”.根据“短板效应”，学生在某个知识点的水平并不取决于该生最擅长的子知识，而是由最薄弱的那部分子知识所决定.比如生A在某一题上错了，并不表示生A对此知识点一无所知，很有可能是在某个更细的子知识点犯了错.为了精准找到这个“病灶”，需要生A再做下一个子知识点的题目，若做对了，就可排除该子知识点，然后去做另一个子知识点的题目；若还是错，则再做下一个子知识点的题，如此递归往复，直至找到真正的原因.因此，每个学生做的测试题量是不一样的.水平高的学生，做对了一题就表明该题包含的知识节点已掌握，接着智能系统就会给出其他知识节点的测试题，因此水平越高的学生做的题越少，水平越低的学生做的题越多.下面呈现部分不同知识节点的测试题.

例如“会判断分段函数的单调性”这个知识点，智能系统给出的测试题之一为：

( )

A.(-∞,-2)∪(2,+∞)

B.(-2,2)

C.(-2,0)和(0,2)

D.(-∞,-2)和(2,+∞)

再如“会解决有关取整函数问题”这个知识点，系统给出的其中一个测试题是：

例2用[x]表示不大于x的最大整数，例如[1.7]=1,[0.25]=0，[-3.4]=-4,则满足方程[3.8x]=[3.8]x+1的自然数x的个数为( )

A.4 B.3 C.2 D.1

再比如知识点“理解新定义”的测试题是：

( )

A.sgn[h(x)]=sgnx

B.sgn[h(x)]=-sgnx

C.sgn[h(x)]=sgn[f(x)]

D.sgn[h(x)]=-sgn[f(x)]

上述例子仅是举了3个知识点的测试题之一，因为同一知识点还有几个变式测试题，以诊断学生究竟错在哪一个子知识点上，从而精准找出学生知识点的短板.

2.2 精准诊断的结果

笔者所研究的实验班有42人参与测试，“分段函数”内容设有32道题，总分为100分.测试结果是平均72分，平均做题为13.57道，每生平均花时30分29秒，全班的诊断雷达图如图1.

图1

由图1可知，学生对分段函数各知识节点的掌握程度并不是均匀公布的，也不是按由易到难的规律分布.因为这16个知识节点从“知道分段函数”开始，按顺时针方向是简单到复杂、基础到高阶来排列的，所以从理论上讲，后面越复杂的知识节点学生应该掌握得越差，然而测试结果并非如此.图1表明，处于中间难度的知识节点，如“解含参的分段函数问题”“解决纳税问题”学生掌握得并不好，而处于后面较难的知识节点，如“知道含取整符号的不等式”“会研究取整函数的图像与性质”等则掌握得很不错.由此表明全班学生测试后掌握知识点的整体状况还是需要仔细分析的，也是值得教师反思的.比如，“会解决纳税问题”的知识节点，学生之所以掌握得不好，原因就是笔者既没有举例讲授涉及分段函数的应用题，也没有让学生练习这类题型，故凡涉及应用背景的测试题学生都没有做好，这显然与教师的“教”有直接关系.而关于“取整符号”和“新定义”这类新题型，教师没有讲过也没有练习，为何涉及前者的知识点学生都做得不错，而后者都做得不好呢？事后访谈得知，原来初中教师已经讲过取整符号这类题型，学生也练习过，因此知道怎么做.由此说明，教师的教学干预还是很有效果的.

下面进一步以接近平均分的某生B为例来呈现个体的诊断情况.

学生B上机测试得了69分，做了17道题，花时33分钟.生B在做完测试题后就可在电脑上直接看到自己的诊断结果，有一张类似图1的雷达图，告诉生B已掌握哪些知识点，哪些没有掌握，并给出了每个知识点班级的平均掌握程度，以清楚自己在班中的位置.随后诊断系统会给出生B的错误类型分析.生B犯了很多记忆方面的错误，有定义记错、性质记错等，同时指出了错误发生在哪类题型上，具体到哪个知识点的定义和性质.再如审题方面的错误，明确告之是分析和观察时出错，具体错误点是“单调区间用并集相连”，即把生B的错误点、错误原因、错误类型精准定位了.显然，智能诊断系统对生B的诊断和评价既客观又有针对性.

2.3 基于精准诊断的精准反思过程

1)学生通过自我反思报告实现精准决策.

每个学生得到自己的诊断图和错误类型分析后，还可进一步查看自己做错的那几道测试题和正确解答，以便学生更清楚地知道自己具体的错误点.另外，智能诊断系统还会给出每个学生的补习路径，明确告诉学生要从哪几个知识点去加强训练.在此基础上教师要求每个学生写出自己的反思报告，具体内容包含做测试题时出错的原因分析与错误类型、改进的实际措施与途径等.

2)教师通过变式训练协助反思落地.

教师事先准备了许多不同知识节点的变式题，有的来自测试系统，有的教师自己编制，而这些变式题的难易度是不同的，以适应不同程度的学生.教师收到每个学生的反思报告后开始介入，首先阅读该生的反思报告，分析该生是否充分借助诊断系统的结果来反思，改进措施是否具有针对性和可操作性；其次考虑学生的数学学习程度，若程度好就提供一些有针对性的较难变式题，相反则简单一些；最后让学生上交自己做的变式题，教师进行面批，使学生的反思决策得到落实.

2.4 精准反思后的二次诊断

学生经过自己写反思报告和做教师提供的针对性变式题之后，对“分段函数”的认识变得更加清晰和深刻，这在后面知识的学习中有所体现.笔者在《数学(必修1)》第一章结束后进行了第二次测试，测试内容是“函数的性质”，希望借助智能系统诊断学生对函数这一章知识的掌握情况.全班的测试结果说明，测试题中凡涉及分段函数的题，如“分段函数的单调性、奇偶性”等，错误率明显降低.

3 关于精准反思的若干思考

3.1 智能诊断为精准反思提供了基础

反思要精准，首先需要精准定位，精准定位源于智能诊断中信息的精准挖掘，而所有信息又来自学生通过上机测试某知识点后的数据收集，然后智能系统经过诊断分析才形成有价值的信息；接着学生根据这些属于自己的信息确定自己知识结构中的薄弱环节和瓶颈位置，最后进行精准决策.由此可见，智能系统的精准诊断为精准反思提供了扎实的基础.

3.2 教学中可采用程序化过程实施精准反思

显然，精准反思是学习者通过智能诊断系统的精准挖掘和分析，得到信息的精准定位后所形成的自我评价，接着作出反思内容与反思措施的精准决策，并在教师协助下通过变式训练使反思落地.因此教师可将整个反思过程进行程序化操作，其流程图如下:

3.3 精准反思能潜移默化地提升学习力

针对高中数学内容的部分核心概念与核心知识进行自我反思，不断地让学生对自己进行评价、监控和调节，并通过教师有针对性地协助，这样可以明显提高学生的反思能力.只要持之以恒，长期坚持，就能在潜移默化中提升学生的反思学习力，进而提高学生的学习力.