平面束定理的证明与教学注记

许海娟

（安庆师范大学 数学与计算科学学院，安徽安庆246133）

数学分析、高等代数以及解析几何是高等院校本科数学的专业基础课程，其中解析几何一般在一年级第一学期开设，它为数学分析中重积分、曲线积分、曲面积分以及高等代数中线性空间、二次型等知识的学习提供必不可少的基础知识，同时将分析、代数中的抽象概念具象化。它的基本思想就是把空间几何结构代数化、数量化，从而使空间中点、线、面具有代数形式，即点有了坐标、曲线及曲面有了方程。当曲线、曲面有了方程以后，就可以进行后续的研究与定量计算[1]，如曲线长度与曲面面积、空间不规则立体体积、非均匀平面薄片质量、非均匀物体的质心与转动惯量、变力沿曲线做功、流体流量的计算等等。

平面束是具有共同性质的平面的集合，其中有轴平面束是最为常用的一类平面束，它方程的建立是平面这一章最核心的内容[2]。平面束定理的证明本质就是建立有轴平面束的方程，在文献[3-5]中均给出了平面束定理的证明，它们的方法主要有向量法、矩阵法、待定系数法。本文主要从直线方程、平面方程本身出发，给出一种新颖的且更加清晰的证明方法，同时纠正文献[3]中平面束定理证明方法的不完备之处和证明过程中的一处错误，最后探讨平面束定理的教学注记，并指出文献[3]和文献[5]中运用平面束定理求异面直线距离存在的问题。

1 平面束定理

定义1[2]具有共同性质的平面的集合叫做平面族。

定义2[2]通过一条定直线的平面族叫做有轴平面束。

定理[2]设两平面：

相交于直线l，则通过l的平面束方程为

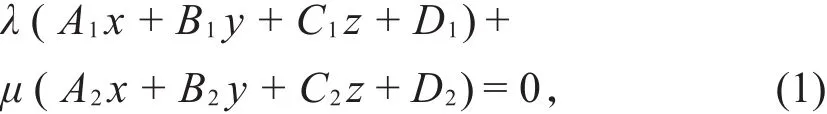
其中λ,μ为不全为零的任意实数。

分析 命题证明需要注意以下两点：(i)方程(1)表示的所有平面都能通过直线l；

(ii)经过直线l的任意平面的方程都能由(1)表示。

证明 (i)直线l的方程为

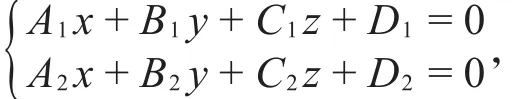
设P(x0,y0,z0)为直线l上任意一点，则

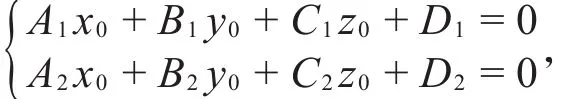
从而

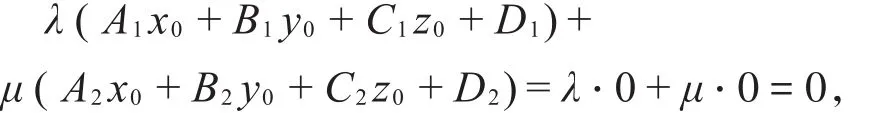
因此点P在(1)式表示的所有平面上，又由点P的任意性知，整条直线l都在(1)式表示的所有平面上。

(ii)设π:Ax+By+Cz+D=0是过直线l的任意平面，它的法向量为n={A,B,C}，平面π1,π2的法向量分别为n1={A1,B1,C1}，n2={A2,B2,C2}，由于向量 n,n1,n2共面，n1,n2不共线，因此根据向量分解定理知：存在唯一一组实数λ,μ，且λ,μ不同时为零，使得：

则

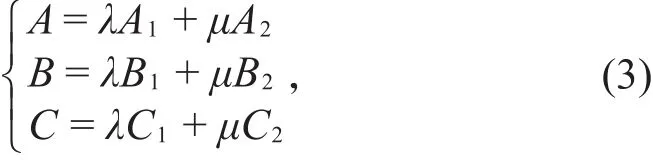
将(3)式代入(1)式中，则平面π的方程变为

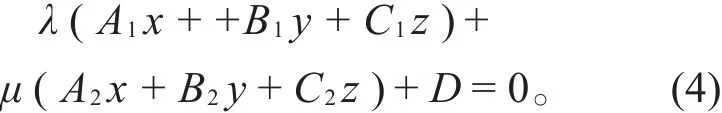
任取直线l上一点P(x0,y0,z0)，则P亦在平面π上，

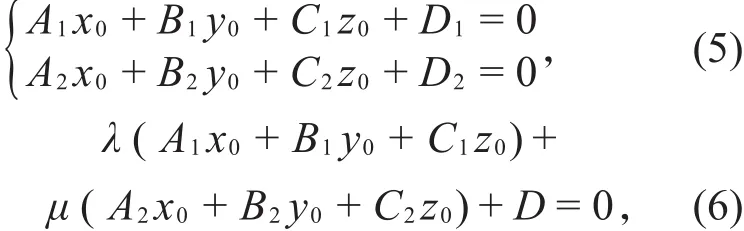
将(5)式代入(6)式中，则有

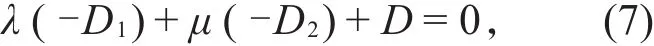
将(7)式代入(4)式中，可得：

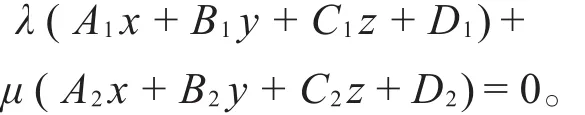
注1根据平面束的定义，平面束定理最本源的问题实际上是证明两个集合相等，而文献[3]中只证明其中一个包含关系，显然是不够完整的。本文采用了更加清晰、直接的方法证明了平面束定理，尤其是第二步（两个包含关系之一）的证明相较于其他方法更简单、易懂。

注2 文献[3]在证明(2)式时，给出λ,μ是不全为零的任意实数这个结论显然是错误的，尽管平面π是任意的，但是一旦平面π取定，根据向量分解唯一性定理，这里的参数λ,μ存在且唯一，并且被π1,π2的法向量唯一确定。

2 平面束定理的应用

平面作为最基本的曲面图形在分析计算中经常遇到，而平面束作为一类具有共同性质的平面的集合具有很多良好的性质，利用平面束的方程可以判定直线与平面的位置关系、计算点到直线距离、求直线在平面上的射影等等。同时，平面作为解析几何、数学分析课程中最常遇到的图形，它在其他方面的应用将在今后专业基础课程教学中不断呈现。这里通过3个例题来展示平面束定理在解析几何上的应用。

例1判定直线l:

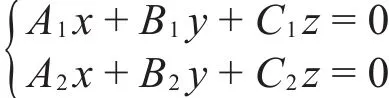
与 平 面 π:(A1+A2)x+(B1+B2)y+(C1+C2)z=0的位置关系。

解 设过l的平面束方程为λ(A1x+B1y+C1z)+μ(A2x+B2y+C2z)=0，即

(λA1+ μA2)x+(λB1+ μB2)y+(λC1+ μC2)z=0，这里，取λ=1，μ=1即是平面π的方程，因此直线l在平面π上。

例2 求直线l:

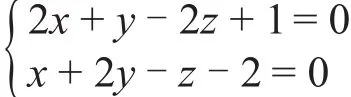
在平面π:x+y+z-1=0上的射影直线方程。

解 先求通过l且垂直于平面π的平面，设过l的平面束方程为

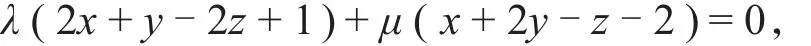
即

(2λ+μ)x+(λ+2μ)y-(2λ+ μ)z+(λ-2μ)=0，于 是 (2λ+μ)+(λ+2μ)-(2λ+μ)=0，所 以λ:μ=2:(-1)，因此所求射影直线方程为

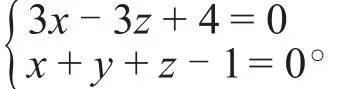
解 点P(3,0,1)到直线l的距离就是它与平面束：λ(x-z+1)+μ(y-2)=0距离的最大值，这里 p0=3,q0=-2,a0=3,b0=4，n1={1,0,-1}，n2={0,1,0}，则有

3 教学注记

在讲授有轴平面束定理过程中需要注意两点：(1)有轴平面束的方程是含有两个参数的，如果用含一个参数的方程，如(A1x+B1y+C1z+D1)+λ(A2x+B2y+C2z+D2)=0，在某些情况下会导致错误结果，因为不论λ取何值时，都将漏掉平面A2x+B2y+C2z+D2=0，而它恰恰应该在平面束中。(2)利用平面束定理去求点到直线的距离完全没有问题，但是如果忽视了异面直线距离与点到直线距离的区别，往往会错误地运用平面束定理去求异面直线的距离，在文献[3]中例2及文献[5]中例3均出现了这个错误，这两篇文献都是在其中一条直线上取一个特殊点再去计算异面直线距离的，正是由于他们忽视了这样取特殊点计算得到的距离是该点与第二条直线的距离，非这两条异面直线的距离。另外，文献[3]中给出的点到直线的距离公式也是错误的。因此在今后的教学过程中，须特别谨慎地处理这些问题，正确地运用好平面束定理。