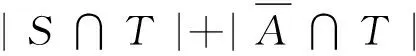不含某类子图的k-连通图中的一个结果
(1、2.安顺学院数理学院, 贵州 安顺561000)
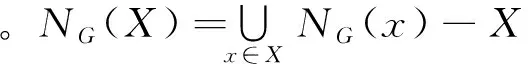
设G是一个k-连通图,T⊂V(G) 是V(G)的一个子集。如果G-T至少有两个连通分支,就称T为G的一个点割集,简称点割。进一步地,若|T|=k,则称T为G的一个k-点割或最小点割。
设G是一个k(≥2)-连通图,e=uv∈E(G)是G中的一条边。对边e进行如下操作:先去掉边e,再将e的两个端点u,v合并为一个顶点,然后将由此产生的所有的“二重边”用一条“单边”来替代,这样,得到一个新图G′。显然,由此得到的新图G′仍然是一个简单图。称e的这种运算为e的收缩(或者称为“收缩边e”)。如果收缩k(≥2)-连通图G中的边e后仍然得到一个k-连通图,那么称e为G的一条k-可收缩边,简称可收缩边。否则,称e为的一条不可收缩边。一个不含任何可收缩边的非完全k-连通图称为收缩临界k-连通图。设G是一个非完全k(≥2)-连通图。显然,若边e=uv∈E(G)是G的一条不可收缩边,当且仅当存在G中的一个最小点割T使得{u,v}⊆T。
设G是一个k-连通图,e是G中的一条不可收缩边,于是存在G中的一个k-点割T,使得e∈E(G[T])。此时若C是G-T的一个连通分支,则称C为G中一个关于e的连通分支。设Y⊂E(G)为E(G)的一个非空子集,T为G中的一个k-点割,若E(G[T]) 中含有Y中的某一条边,这时称G-T的任一个连通分支C为G中关于Y的连通分支。
若一个图G没有子图同构于图H,称G是一个“不含H的图”。同时称H为G的一个“禁用子图”。
1 一些相关结论
1981年,Thomassen[2]证明了下面的定理:
定理1 一个不含三角形的k-连通图含有一条k-可收缩边。



Ando等[5]证明了如下定理:




(i) 若δ(G)≥k+1,则G中每一个点都关联一条k-收缩边;
(ii) 若G中任意两个相邻的点x,y都满足dG(x)+dG(y)≥2k+1,则G中的每一个k度点都关联一条k-可收缩边。
由定理4(ii),我们立即可推出下面的结论:



这里需要说明的是,尽管Ando等[5]在证明过程中假定了k≥4为偶数,实际上当k>4为奇数时,该证明(对命题2)仍然有效,命题2的结论仍然正确。故在命题2中对k(≥4)不再限制其奇偶性。实际上,对命题 2,可以将整数考虑到k≥3。于是,进一步地,有下面的结论(在此不妨称其为定理 5)。

2 定理 5 的证明

断言1 若dG(x)=3,则|E(x)∩M|≥1。若|E(x)∩M|=1,设xy∈(E(x)∩M),则xy是G中的一条3-可收缩边。


定理 5 的证明。
令F=E(x)∩M。则当dG(x)≥4时,由题设条件总有|F|≥2。当dG(x)=3时, 若|F|=1,由断言1可知x关联一条可收缩边,这时,结论正确。于是,当dG(x)=3时,总假定|F|=3。这样,无论何种情形,总有|F|≥2。
证明E(x)中至少含有一条3-可收缩边:

|A∪S|≥|NG(a)∪NG(b)|=|NG(a)|+
|NG(b)|-|NG(a)∩NG(b)|≥3+3-1=5。即,



ASABTBA∩BS∩BA∩BA∩TS∩TA∩TA∩BS∩BA∩B
图1
首先证明A⊂T。