数学文化试题高考展望

黄昆耀

《考试大纲》强调数学试题需要展现数学的科学价值和人文价值.数学文化题主要取材于数学时事、数学名著、数学名人、数学游戏、数学命题、数学猜想、数学图形等.

一、数列问题

例1 《算法统宗》是明朝程大位所著数学名著，其中有这样一段表述：“远看巍巍塔七层，红光点点倍加增，共灯三百八十一.”其意大致为：有一座七层宝塔，每层悬挂的红灯数为上一层的两倍，共有381盏灯.该塔中间一层有（ ）盏灯.

A.24

B.48

C.12

D.60

小结本题以明朝程大位的《算法统宗》中的一首歌谣为背景，考查等比数列的概念及其求和公式，考查学生分析问题的能力与转化的能力.

练习1 我国古代数学名著《九章算术》中，有已知长方形面积求一边的算法，其方法的前两步为：

二、立体几何问题

例2《九章算术》是我国古代内容极为丰富的数学名著，系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”.若某“阳马”的三视图如图1所示（单位：cm），则该“阳马”的外接球的体积为

小结本题以《九章算术》中的问题为材料，试题背景新颖.解答本题的关键是通过补形，正确画出直观图，外接球的直径就是长方体的体对角线.

练习2 “牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中，构造的一个和谐优美的几何体.它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）.其直观图如图3，图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时，它的俯视图可能是

三、框图问题

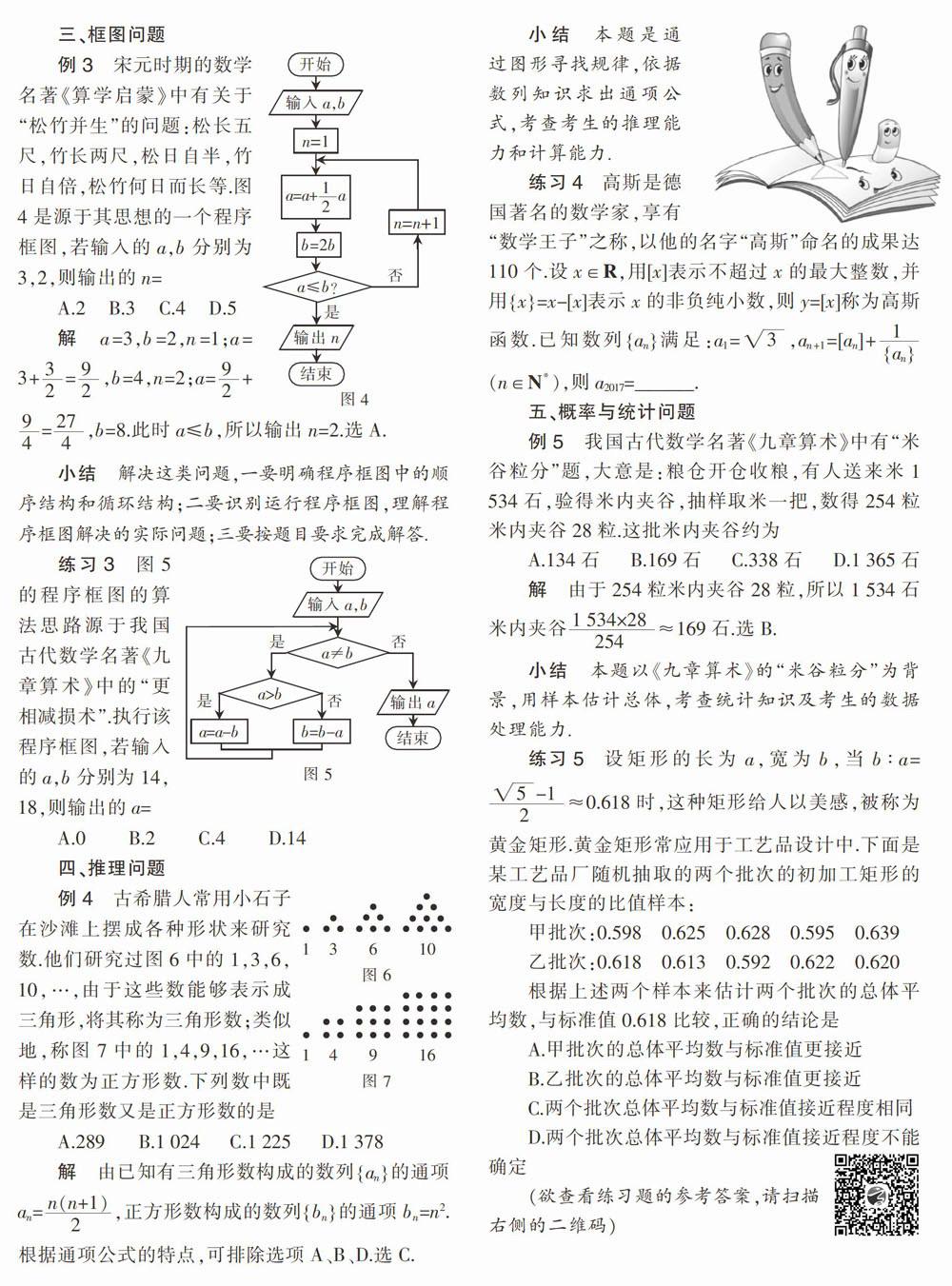
例3宋元时期的数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松目自半，竹日白倍，松竹何日而长等.图4是源于其思想的一个程序框图，若输入的a，b分别为3，2，則输出的n=

小结 解决这类问题，一要明确程序框图中的顺序结构和循环结构：二要识别运行程序框图，理解程序框图解决的实际问题：三要按题目要求完成解答.

练习3 图5的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图，若输入的a，b分别为14，18，则输出的a=

A.O

B.2

C.4

D.14

四、推理问题

例4古希腊人常用小石子在沙滩上摆成各种形状来研究数.他们研究过图6中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数：类似地，称图7中的1，4，9，16，…这样的数为正方形数.下列数中既是三角形数又是正方形数的是

A.289

B.1 024

C.1 225

D.1 378

小结 本题是通过图形寻找规律，依据数列知识求出通项公式，考查考生的推理能力和计算能力.

五、概率与统计问题

例5我国古代数学名著《九章算术》中有“米谷粒分”题，大意是：粮仓开仓收粮，有人送来米1534石，验得米内夹谷，抽样取米一把，数得254粒米内夹谷28粒.这批米内夹谷约为

A.134石 B.169石 C.338石 D.1 365石

小结 本题以《九章算术》的“米谷粒分”为背景，用样本估计总体，考查统计知识及考生的数据处理能力.

练习5设矩形的长为a，宽为b，当b：a=V 5—i。0.618时，这种矩形给人以美感，被称为

2黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取的两个批次的初加工矩形的宽度与长度的比值样本：

甲批次：0.598 0.625 0.628 0.595 0.639

乙批次：0.618 0.613 0.592 0.622 0.620

根据上述两个样本来估计两个批次的总体平均数，与标准值0.618比较，正确的结论是

A.甲批次的总体平均数与标准值更接近

B.乙批次的总体平均数与标准值更接近

C.两个批次总体平均数与标准值接近程度相同

D.两个批次总体平均数与标准值接近程度不能确定