基于比赛工况的巴哈赛车车架设计与优化

孔超，王正伟，杨国玮，陈淼



基于比赛工况的巴哈赛车车架设计与优化

孔超1，王正伟2，杨国玮1，陈淼1

（1.天津职业技术师范大学汽车与交通学院，天津 300222；2.寿光职教中心，山东 寿光 262700）

基于巴哈比赛规则利用Catia软件设计了用于巴哈大赛的赛车车架，将模型导入ANSYS Workbench进行分析，结合比赛工况进行力学分析发现，在满载弯曲、V字沟、乱石路况及牵引工况下，强度满足设计要求；但刚度分析中发现刚度较低；进行自由模态和约束模态分析发现，自由模态第四阶频率与发动机振动频率接近，容易发生共振。通过增加三角形稳定结构优化后侧向防撞构件和防滚环的方式提高车架扭转刚度和固有频率，再次分析满足设计要求。

赛车车架；比赛工况；强度；刚度；模态

前言

中国汽车工程学会巴哈大赛（以下简称巴哈大赛）是由中国汽车工程学会于2015年创办的主要面向职业院校和本科院校开展的小型越野汽车设计和制作赛事。大赛要求各参赛车队在规定时间内使用同一型号发动机设计制造一辆单座、中置后驱的小型越野车，参加多种静态与动态项目测试[1,2]。静态项目包括技术检查、赛车设计、成本与制造等，动态项目包括牵引力测试、爬坡测试、直线加速测试、耐力测试等。

车架作为赛车最重要的部分之一支承赛车所有簧上质量，在动态项目中，车架要承受各比赛工况下路面反馈的复杂载荷的同时受到外部激励，因此要确保车架有足够的强度和刚度的同时行驶中不产生共振。根据比赛规则和经验设计了巴哈赛车车架，利用有限元法对强度、车架扭转刚度及车架模态进行了分析和优化。

1 车架设计

通过合理设计和加工，车架可以在发生危险情况时防止驾驶员受伤。车架的设计首先要遵从《中国汽车工程学会巴哈大赛规则》，满足布局合理、有足够的强度与刚度、良好的人机工程性能及轻量化的要求，主要由防滚架、牵引悬挂点、各总成安装支架以及悬架安装吊耳等部分组成。近年来，巴哈赛车多数使用桁架式车架，该类车架主要用于竞赛汽车和特种汽车，兼有车架和车身的作用，一般由钢管组合焊接而成[3-5]。利用Catia软件设计的赛车车架如图1所示。

图1 赛车车架

2 比赛工况下力学分析

利用ANSYS Workbench软件对赛车车架进行有限元分析[6-8]，分析车架强度和刚度，检验是否能够承受疲劳载荷的同时变形量负荷要求。

2.1 车架模型的前处理

前处理包括对车架模型的简化、材料属性及单元横截面的设定、定义接触、网格划分，需要通过对车架模型的简化提高计算速度。设定车架材料为铬钼钢，其力学性能如表1所示。

表1 4130铬钼钢管力学性能

根据车架主要结构件和次要结构件受力情况设定构件壁厚，结构件间定义为绑定接触，采用网格全局控制、四面体网格，对集中受力的地方进行网格局部加密，部分网格划分加密如图2所示。

2.2 车架强度分析

车架强度分析主要针对赛车在比赛工况行驶时车架应力及变形情况，比赛工况四种：满载弯曲、扭转、紧急制动及牵引工况。

2.2.1满载弯曲分析

该工况分析车架在加载全部载荷下良好路面上行驶时车架应力、应变等。满载荷弯曲下车架所受载荷有：车架自重、驾驶员及座椅、发动机、变速器和传动机构及其他总成所产生的重力等。对车架与悬架连接点进行位移约束后分析，车架的应力状态图、变形状态图、应变状态图如图3所示。

图3 车架满载弯曲分析

可知：车架最大应力主要集中在座椅位置，应力为36.968MPa，远小于车架材料的许用应力；位移变形最大值为0.18295mm，位置为座椅安装处，位移量远远小于最大允许位移量，满足设计要求。

2.2.2扭转分析

巴哈赛车耐久赛赛道全地形道路包括乱石堆、轮胎阵、V字沟、飞坡、泥坑等，赛车在该赛道行驶时车架扭转变形较大。本处主要分析赛车在全地形道路下车架的受力和位移变形。

V字沟路况下的应力状态、变形状态、应变状态如图4所示。

图4 V字沟路况下的应力状态、变形状态、应变状态

可以看出V字沟路况下车架的最大应力主要集中在座椅位置及后部防滚环底部，最大应力值为64.785MPa，远小于车架材料的许用应力；车架的位移最大值为0.66354mm，最大位移位置为座椅安装处，位移量远远小于最大允许位移量，满足设计要求。

图5 乱石堆路况下的应力状态、变形状态、应变状态

乱石堆路况下，赛车在行驶过程中右后车轮会出现悬空情况，前轴载荷全部加载在右前车轮处，因此重新设定约束条件和加载情况进行计算。该路况下的应力状态、变形状态、应变状态如图5所示。

在乱石堆路况下车架的应力主要集中在车架的前部，应力集中处的应力为68.759MPa，远小于车架材料的许用应力；车架在乱石堆路况下的最大位移变形值为0.7389mm，位置为车架前部，位移量远远小于最大允许变形量，满足设计要求。

2.2.3紧急制动

赛车遇到危险情况时不可避免进行紧急制动，此时车架除了承受重力外还承受巨大的惯性力，车架上载荷分布迅速变化，因此分析车架在进行紧急制动时的应力、位移变形及应变是必要的。应将前后悬架和车架连接点位移进行约束。该路况下的应力状态、变形状态、应变状态如图6所示。

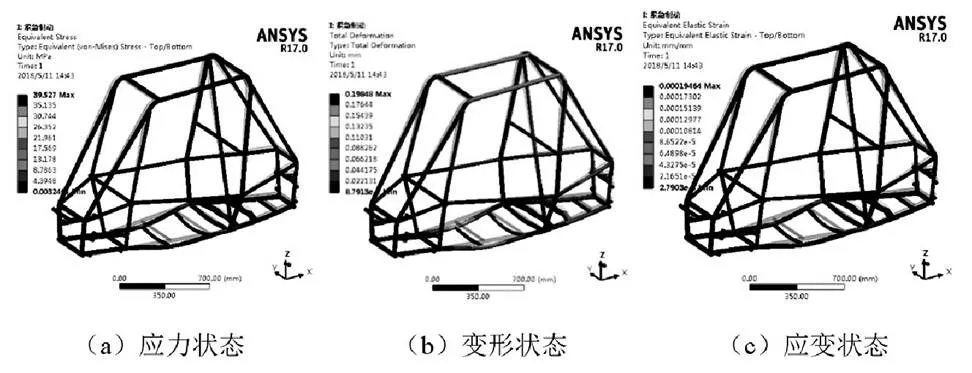
图6 紧急制动下的应力状态、变形状态、应变状态

紧急制动下车架的座椅位置应力最为集中，为39.527 Mpa，远小于车架材料的许用应力；车架在该分析下的最大位移值为0.19848mm，为座椅安装位置，远小于最大允许位移量，满足设计要求。

2.2.4牵引工况

赛车有爬坡或牵引赛事，爬坡被设计为测量车辆对路面传送额外（攀爬）力量的能力。如果当地形不支持爬坡，则可以采用牵引赛事进行替代，此时赛事设计为使车辆牵引一个大负荷。牵引工况下车架所受载荷为：牵引力、车架自重、驾驶员及赛车自身各总成所产生的重力等。设定边界约束和载荷后进行分析，该路况下的应力状态、变形状态、应变状态主要为车架尾部，分析结果如图7所示。

该工况下车架的后方牵引点应力最为集中，应力为96.175MPa，远小于车架材料的许用应力；车架在该分析下的最大位移为0.72641mm，为车架后部牵引点，位移量远远小于最大允许位移量，满足设计要求。

2.3 车架刚度分析

评价车架刚度的标准主要包括：弯曲刚度、扭转刚度等，大赛规则中规定采用车架的扭转刚度作为其刚度设计的评估标准。使用ANSYS计算车架的扭转刚度。设定边界约束和载荷后进行扭转刚度计算，结果如图8所示。

经计算，车架的扭转刚度约为5069 N·m/deg，根据经验赛车扭转刚度一般在5500 N•m/deg 到8000N•m/deg之间，因此车架扭转刚度需优化提高。

3 车架模态分析

赛车行驶中车架受到外界激励会发生振动，当激振频率与车架固有频率接近时车架会发生共振，严重时会使车架发生扭曲变形甚至使车架管件断裂，极大的影响行驶安全，因此设计过程中对车架进行模态分析是必要的[9,10]。针对车架进行了自由模态和激振模态分析，分析过程包括：模型导入、求解和结果后处理。分别求解自由状态下和约束状态下模态得到车架一至六阶固有频率。计算结果如表2所示。

表2 模态分析

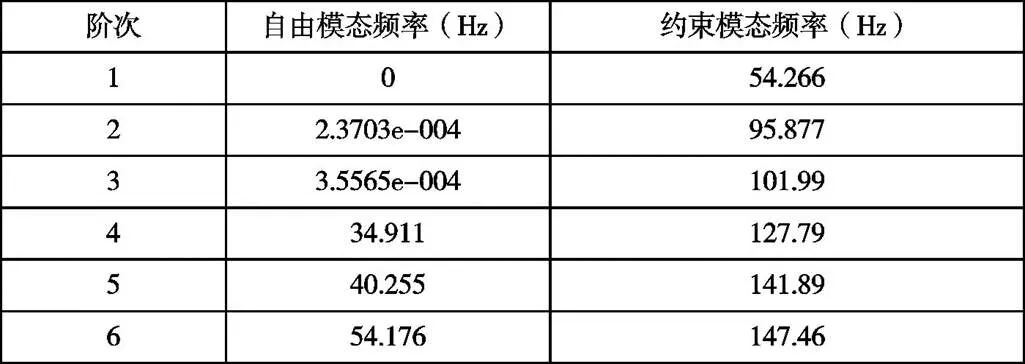
比赛过程中，外界对车架的激励主要来自于路面白噪声和发动机振动。路面白噪声对车架的激励频率取决于路面情况，巴哈赛车比赛时的道路为越野赛道，对车架的激励频率在5到20Hz之间；经计算，发动机工作时引起的激振频率介于17-32Hz之间。车架自由模态下第四阶振型频率接近发动机工作时激振频率，容易引起车架与发动机共振。车架自由状态下的其他振型频率均与32Hz相差较大，不会引起车架共振。车架约束模态的固有频率从第一阶到第六阶均在32Hz以上，也不会引起共振。因此，需车架提高自由模态下低阶频率。

4 车架优化

车架应从提高车架刚度和提高车架固有频率两方面入手。

4.1 提高车架扭转刚度

提高车架扭转刚度一般可采用提高材料的力学性能、减小车架宽度及采用更多的三角形稳定结构的方式。4130铬钼钢管的力学性能较优，更换材料势必带来成本提升；减小车架的宽度则牺牲了驾驶舱本就拥挤的空间，过窄的车架会影响驾驶员操作；采用三角形结构可以加强车架的结构，车架总体质量增加，但对比赛结果影响较小，因此采用更多的三角形稳定结构提高刚度。在防滚架侧向防撞构件位置增加三角形稳定结构，如图9所示。

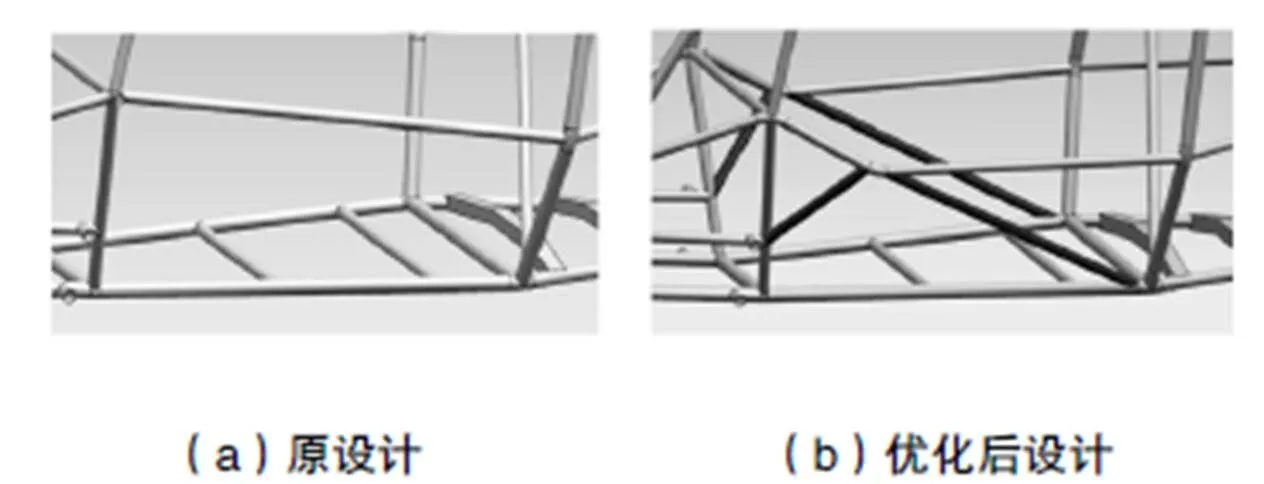
图9 防滚架侧向防撞构件位置增加三角形稳定结构

将优化后设计重新进行扭转刚度计算，结算结果如图10所示。

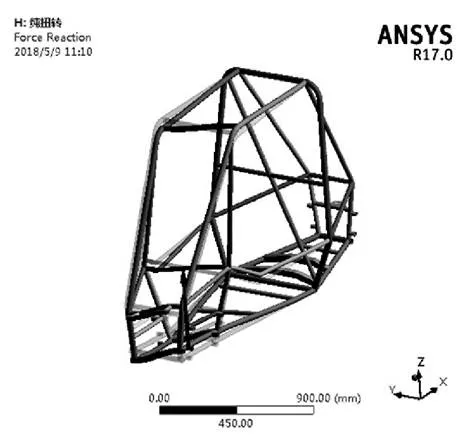
图10 优化后车架扭转变形

利用软件探针功能求出左右前悬架与车架连接点处的约束反力后进行计算，得到扭转刚度为7063.2 N•m/deg，满足要求且处于较高水平。

4.2 提高车架固有频率

通过改进防滚架侧向防撞构件，改进前部防滚环构件改变车辆固有频率。如图11所示。

图11 优化后侧向防撞构件和防滚环

进行自由和约束模态分析后，结果如表3所示。

表3 优化后模态分析

优化改进后车架自由状态下固有频率的低阶频率为46.079Hz，高于赛车工作频率32Hz以上，车架固有频率提高约35.3%。

优化后巴哈赛车车架的刚度及固有频率较之前都有了明显提高，将综合两种改进作为车架的最终设计方案，如图12所示。

图12 最终设计方案

5 结论

作为巴哈大赛赛车重要的部件，车架承载着所有的簧上质量，对于赛车性能有着重要的作用。

5.1利用Catia软件设计了符合比赛规则的巴哈赛车车架；

5.2利用ANSYS Workbench软件进行了比赛工况下车架力学性能分析，结果显示，扭转刚度不符合要求；进行自由模态和约束模态分析，发现第四阶自由模态和发动机激振频率接近；

5.3通过增加三角形稳定结构优化后侧向防撞构件和改进防滚环的方式提高车架扭转刚度和固有频率，再次分析满足设计要求。

[1] 柯怡达.2015中国汽车工程学会巴哈大赛完美落幕[J].汽车与配件,2015(40):77-81+76.

[2] 百力通为中国汽车工程学会首届巴哈大赛赞助发动机[J].汽车与配件,2015(36):19.

[3] 倪晓菊. 大学生方程式赛车车架研究[D].南京理工大学,2016.

[4] 乔邦.基于有限元分析的大学生方程式赛车车架结构强度优化[D].河南科技大学,2012.

[5] 周永光,阳林,吴发亮,邓仲卿.FSAE赛车车架结构优化和轻量化[J].农业装备与车辆工程,2012,50(11):37-41.

[6] 宁连旺.ANSYS有限元分析理论与发展[J].山西科技,2008(04): 65 -66+68.

[7] 陈宾.基于FSAE整车动力学仿真的车架CAE分析及优化[D].长安大学,2013.

[8] 牛华.基于有限元的FSAE车架刚度及强度分析[J].黑龙江科技信息,2016(33):79.

[9] 王新彦.基于ANSYS的越野赛车车架模态分析[J].拖拉机与农用运输车,2009,36(04):28-29+32.

[10] 高棱,潘锦强,谢楚森,蔡桂杰.基于ANSYS的FSAE车架模态分析与验证[J].煤矿机械,2016,37(05):172-174.

Design and Optimization of Baja Racing Car Framebased on Race Conditions

Kong Chao1, Wang Zhengwei2, Yang Guowei1, Chen Miao1

（1.Tianjin University of Technology and Education, Tianjin 300222; 2.Shouguang Vocational Education Center, Shandong Shouguang 262700）

Based on the rules of the Baja SAEChina, the car frame used in Baja competition was designed by using Catia. The model was introduced into the ANSYS Workbench, and the mechanical analysis was carried out to find out the strength under the full load bending, the V groove, the stoulding road condition and the traction condition. The free modal analysis and constrained modal analysis show that the fourth order frequency of the free mode is close to the engine vibration frequency and is easy to generate resonance. The torsion stiffness and natural frequency of the frame are improved by increasing the lateral anti collision member and anti roll ring after optimizing the triangle stability structure, and the design requirements are met again.

racing car frame; race conditions; strength; stiffness; modality

B

1671-7988(2018)16-146-04

U463.8

B

1671-7988(2018)16-146-04

CLC NO.: U463.8

孔超（1983.7-），男，现就职于天津职业技术师范大学，讲师，硕士研究生，主要研究方向：车辆工程，汽车职业教育。

10.16638/j.cnki.1671-7988.2018.16.052