例谈运用转化思想解析复杂几何图形面积问题——五年级上册“组合图形面积”的教学实践与思考

江苏扬州市梅岭小学西区校（225000）

学习了求组合图形面积的方法之后，学生都能按照常规思路用割补法和增补法求出面积，然而这些基本方法只适用于一些常见题型，一旦碰到棘手的难题，学生往往束手无策。对此，笔者给出了一些解题方法，以引导学生用转化的思想解答复杂的几何图形面积问题。

一、铺垫引入

师：下列图形可以分割成哪些基本的平面几何图形？

生1：图1可分割成梯形和长方形，图2可分割成三角形、长方形和梯形各一个。

图1

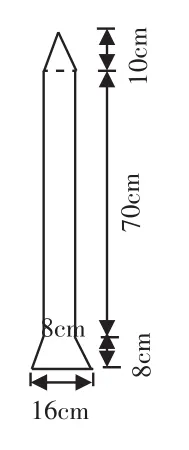
图2

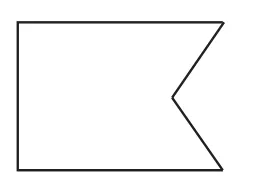
图3

生2：图3可以分割成两个梯形。

生3：还有一种分割方案，将图3分成一个长方形和两个三角形。

生4：图3补一块就能成为大长方形。

师：由几个简单的规则几何体有机组合构成一个较为完整的新图形，称为组合图。今天我们就来研究组合体的面积问题。

二、合作探究

师（出示问题）：小明家的客厅形状如图4所示。要在这间客厅上铺满地砖，地砖的总面积为多少？先估算再笔算。

师：小明家如果购进42平方米的地砖材料，浪费吗？请先独立帮小明做预算，然后在组内共同探究。

（学生独自解答，教师巡视指点）展示具有代表性的学生作业：

图4

图5

师（指着①）：请说说解题思路。

生1：我采用的是切分法。把组合体分成长方形和正方形两个单体，然后分别求出长方形和正方形的面积。观察对比图形中的各条线段可知，长方形长6m、宽4m，面积为6× 4=24（m2），正方形面积为3× 3=9（m2），所以24+9=33（m2）。

师（指着①）：凭什么判断右侧的矩形是正方形？

生2：右侧图形的长边为7m减去4m，等于3m，与邻边等长。

师（根据学生的口述内容板书：6×4+(7-4)×3=33（m2）；指着（7-4））：判断是长方形还是正方形关键就看这里！

师：①被切分成两个矩形，这种称为分解法，还有哪几幅图用到了分解法？

生3：②③④⑤⑥均是采用分解法。

（教师追问能否计算⑥的面积，学生说能，并迅速将该图形分拆成三个三角形；当教师等比例放大图形后，学生改口说不行，理由是放大后可以分辨出得不到三个三角形）

师：拆分⑥对切割线有着严格限制，这个姑且不论，继续看②③④⑤。

学生汇报展示：

图6

生4：这里都用了分割法，先求出各分图面积，再求出总图面积。

师：我们用五种方法成功帮助了小明，得到面积为33平方米。你觉得哪种方法更好？

生5：我觉得①②③最简便，因为只分成2个单图，而④和⑤分出了3个单图。

师：不错，分得的单图越少越好。

师（指着⑦）：这题有什么不同之处？

生6：计算的时候，可以先在⑦的右上角补一块，构成长方形，算了长方形的面积后再还原，6×7-3×3=33（m2）。

师：这种方法称为增补法。

师：如果综合应用分切法和增补法，可行吗？

生7（上台作图演示）：把上部凸出的一块剪切下来，拼接到左边，形成一个新的长方形，长为7+4=11（m），宽是3m，面积是11× 3=33（m2）。

图7

师：这种综合法称为割补法。

三、巩固延伸与总结

第一关：运用割补法或分割法，转化下列各图。

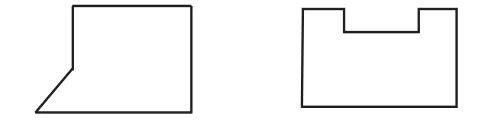
图8

第二关：计算一面队旗的面积。

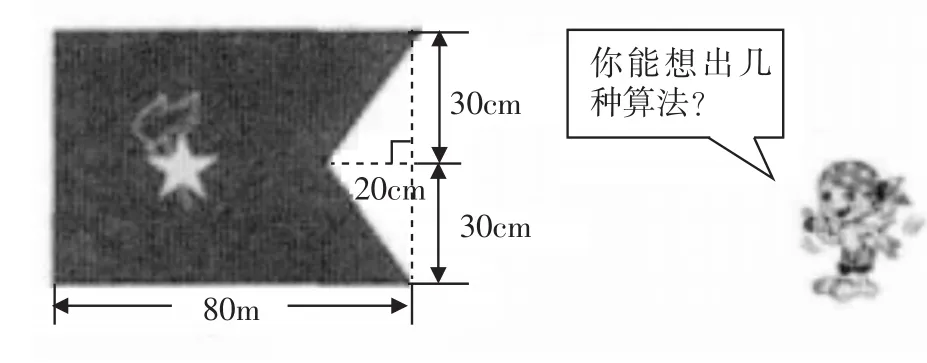
图9

第三关：求阴影部分的面积（单位：dm）

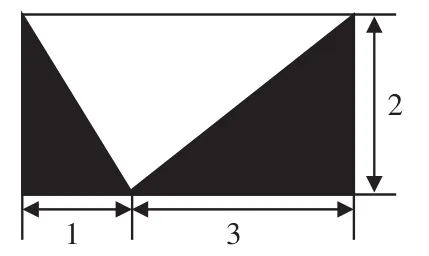
图10

四、小结

师：利用切分法或增补法，可把组合体分解成若干个单体，再用加减法求面积。要强调的是，解题时要因地制宜灵活选用分解方法。

数学思想是数学的灵魂，而转化思想更是灵魂中的精髓。在教学“组合图形面积”时，转化可以将复杂问题简单化，将不可能转化为可能，实现策略最优化，从而促进学生提升整合知识的能力，训练学生思维的灵活性。