细节浸润：让数学和声课堂鲜活起来——以三年级上册“周长”一课为例

重庆市渝中区人和街小学（400015）

老子曰：“天下大事必作于细,天下难事必作于易。”汪中求说：“大理不辞小让，细节决定成败。”由此可见细节的重要性。数学教学也不例外。下面结合人教版教材三年级上册“周长”一课的教学，探析如何在教学中浸润细节，让数学课堂鲜活起来，实现小学数学和声课堂。

一、细读教材，握准“四基”“四能”“四维”是数学和声课堂鲜活的基础

《义务教育数学课程标准（2011年版）》指出：“数学教材为学生的数学学习活动提供学习的主题、基本线索和知识结构，是实现数学课程目标、实施数学教学的重要资源。”细读教材是设计教学的根本。细读教材包括读懂教材的编排意图，读懂教材蕴含的“四基”“四能”“四维”。例如人教版教材三年级上册“周长”一课是这册内容的起始课，是学生认识了由直的边围成的封闭图形（如三角形、长方形和正方形等）的基础上学习“什么是周长”，从而为学习计算长方形和正方形的周长做铺垫,更为以后学习各种图形的周长及面积的计算方法做准备。为了让学生更好地理解“周长”的概念，教材呈现了一些规则或不规则的实物和图形（如树叶、三角尺、数学书封面、钟面等实物图和五角星、三角形、长方形、正方形等图形），旨在帮助学生直观理解周长的一般含义，即封闭图形一周的长度。最后，教材“小精灵”提出：“有办法知道上面这些图形的周长吗？”，并呈现学生探索图形周长的活动场景，目的是让学生动手探索一般图形的周长，进一步感悟周长的实际含义，为求规则图形的周长做准备。教材安排的“做一做”练习中有4道习题：判一判、描一描，算一算，辩一辩，量一量。从教材的编排不难看出，“周长”一课所承载的“四基”“四能”“四维”。

1.教材中承载的“四基”

《义务教育数学课程标准（2011年版）》指出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”基础知识就是周长的概念；基本技能就是通过比一比、指一指、摸一摸、描一描、判一判、算一算等步骤让学生理解、归纳、概括周长的意义；教材渗透了比较、化曲为直、等量变换、转化的数学思想；数学活动是学生通过实际操作测量规则图形（如三角形、长方形、正方形）和不规则图形（如树叶、巧克力、头围、胸围、腰围）的周长的过程中获得数学活动经验。

2.教材中承载的“四能”

《义务教育数学课程标准（2011年版）》指出：“增强发现和提出问题的能力、分析和解决问题的能力。”教材充分考虑了“四能”的培养，按照“发现问题—提出问题—分析问题—解决问题”的思路编排。教师在教学时可先设置情境让学生理解“一周”，然后呈现“小精灵”的问题：“有办法知道上面这些图形的周长吗？”学生通过操作解决问题，以及完成巩固概念的基本练习（“做一做”的习题和练习十八的1、2题）、辨析概念的相应题组（练习十八的第3题），加深了对周长概念的理解，体会了图形转化的方法，增强了对数学学习的兴趣。

3.教材中承载的“四维”

《义务教育数学课程标准（2011年版）》指出：“为使每个学生都受到良好的数学教育，数学教学不仅要使学生获得数学的知识技能，而且要把知识技能、数学思考、问题解决、情感态度四个维度的目标有机结合，整体实现课程目标。”“周长”这一课的“四维”可以概括如下：

（1）通过比一比、指一指、画一画等数学活动，学生初步理解周长的含义。

（2）通过测量（实测和估测）图形（物体面）的周长，培养测量技能，积累测量的操作经验，培养空间观念和抽象概括能力，让学生感受等量变换思想。

（3）让学生感受测量周长在现实生活中的应用，体验测量的价值，增强学生学习数学的积极性。

综上所述，以“什么是周长”为线索，将教学思路定格为“设置情境，理解‘一周’——自主探索，聚焦疑点，发现差异，理解周长的本质——寻求突破，达成共识，深化周长的概念课堂小结，总结学习收获”。

二、关注每个环节的设置是数学和声课堂鲜活的关键

所谓细节，就是教学中不易发觉的细微之处，它有时会成为教学的闪光点，成为学生思维的转折点，它有时会成为教学的突破点，成为学生学习习惯的开启点。

1.关注设置情境的细节,人人参与，让学生愉快地学

通过设置情境，可引发学生思考，让学生发出声音，提出见解，激发学生的学习欲望。

【教学片段1】理解“一周”的情境设置

【方案A】

师：一年一度的森林运动会又开始了，现在进行比赛。（课件出示：小动物在草地上准备比赛的场景）他俩谁会获得冠军呢？（课件出示：小动物赛跑的过程；兔子获得冠军）为什么是兔子？

生：因为小动物都是绕草地跑了一圈，兔子最先跑完，所以他获得冠军。

师：说得真好！小动物都是从起点出发又回到了这个起点，刚好绕草地跑了一周，一周的长就是这块草地的周长。（课件闪烁显示草地的周长部分）这节课，老师和大家一起来研究平面图形的周长。

【方案B】

师：小强要减肥，爸爸制订了一个锻炼计划，让他每天围着操场跑一圈，我们去看看他是怎么跑的。

（课件动态演示：第一次跑）

师：他跑对了吗？

师：应该沿着操场的哪里跑？

师：这条黑黑的线也就是操场的边线。

师：如果你是小强的爸爸，你会对小强说些什么？

（课件动态演示：第二次跑）

师：第二天，小强又开始出发了。

师：小强这回跑完一圈了吗？

师：你来指指应该跑到哪里？

（课件动态演示：第三次跑）

师：第三天让我们陪着小强一起跑，好吗？伸出小手，一起出发，一起喊停。出发！

（指出：围着操场跑一圈也可以说成围着操场跑一周）

【方案C】

师：小强是我们班的同学，他要减肥，爸爸给他制订了一个锻炼计划，让他每天围着操场跑一圈（出示400米标准操场图），我们去看看他是怎么跑的。

师：小强跑的方式和你想的一样吗？

生1：不一样。

师：谁来说一说怎么不一样。

生2：小强沿着边线跑但只跑了大半圈，没有跑完。

师：你觉得他应该跑到哪里呢？请给大家指一指。

生2（边指边说）：他应该跑到起跑的那个地方。

师：小强虽然是沿着边线跑的，但从起点开始跑后，最后还要回到这一点上，对吗？那我们拿出小手跟着小强一起跑好吗？（教师出示课件，学生边喊边用手比画，充分理解“封闭图形”和“一周”）

方案A虽然是由森林运动会引入课题，有利于激发学生的学习兴趣，使学生产生亲切感，符合学生的年龄特点，能自然地引出“周长”这个学习课题，并为下一步的学习做好铺垫，但是学生对“一周”的理解不够深刻。

方案B则是呈现学生在操场跑步的情景，既富有童趣又贴近学生的生活经验。通过三次动画演示，激发和调用学生“跑一圈”的生活经验，学生能够初步感知“边线”“封闭”(起点出发回到起点)，为学习“周长”奠定基础，为理解“封闭图形”“一周的长度”做好铺垫。

方案C设置的情境更具有目的性，由“大圈——一圈”，学生对“只要是封闭图形就有周长”的理解更为深刻，对“封闭图形”“一周”的认识就有直接突破，看似小小的变化，实际是教师对教材解读的又一次质的飞跃。

2.关注发现差异的细节，寻求共识，让学生会学

差异，指区别;不同。发现差异对于和声课堂而言,首要手段就是倾听，也就是要细心听取每一个人的意见，并从中发现其细微之处。如何在本课中关注差异，激活学生的思维，完成课堂教学目标呢？

【教学片段2】

师：公园里有两块不同形状的草坪，请指一指它们的周长。仔细观察，它们的周长一样吗？

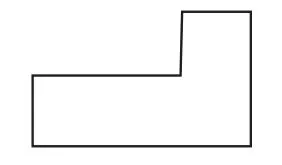
图1-1

图1-2

生1：不一样长，因为看起来图1-1要小一些。

生2：一样长。

师：为什么？能说说你的想法吗？

生2（指着图比画）：这两个图形的一条长边和一条宽边是相等的。将图1-1的这线段平移到这里，又将这条线段平移到这里，图1-1就变成了一个长方形，长方形的对边相等，所以它们的另一条长边和宽边和图1-2的长方形的长边和宽边也相等，因此两个图形的周长一样长。

师：就像这位同学说的，这两个图形的一条长边和一条宽边是相等的，通过平移这两条短的线段，图1-1就变成了一个长方形，因为长方形的对边相等，所以这两个图形的周长就一样长。

从这个教学片段不难看出，学生之间的差异是很明显的，生1直观感觉到第一个图形的周长要小一些，对周长概念的理解还不是很深刻，而生2真正理解了周长的本质含义，通过平移知道两个图形的周长一样长。显然，学生对转化思想（平移）的认识是肤浅的，教师应该让习题充分发挥出它的价值，让每个学生的思维得到提高。

3.关注聚焦疑点的细节，达成共识，让学生学会

疑点主要指差异背后实际存在的矛盾点和冲突点，是差异之所以存在的根本原因，疑点也是接近问题的关键点和突破点，是思维的聚焦点。对于教学片段2，我们做了以下改进。

【教学片段3】

（1）比一比，让学生理解概念的本质

师：这两个图形的周长一样吗？你是怎样想的？观察这两个图形，它们有什么相同的地方和不同的地方？

图2-2

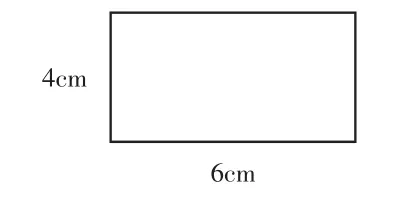
图2-1

生1：两个图形都是封闭图形。

生2：图2-1的长方形比图2-2的图形看起来要大一些。

师：同学们真会观察和思考，总结也非常精彩。这两个封闭图形的周长谁更长呢？

生3：图2-1的长方形的周长比图2-2的图形周长要长一些，因为看起来图2-1的长方形要大一些。

生4：因为封闭图形的周长是它一周的长度。将图2-2的图形的两条边分别向上和向左平移，就得到和图2-1一样的长方形，所以两个图形的周长一样。

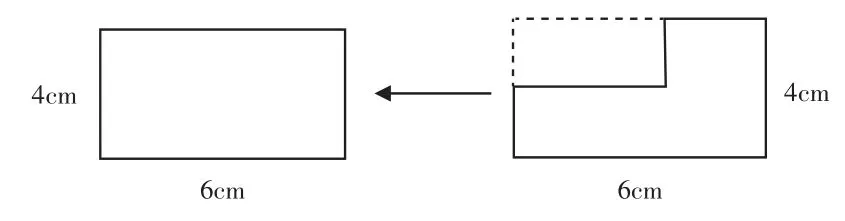
图3

师：看来，要弄清这两个图形的周长，不能被表面现象所迷惑，要从本质上去理解、分析。周长就是——

生（齐）：封闭图形一周的长度。

（2）变一变，培养学生的思维深刻性

A.下面每组图形的周长一样吗？你是怎么想的？

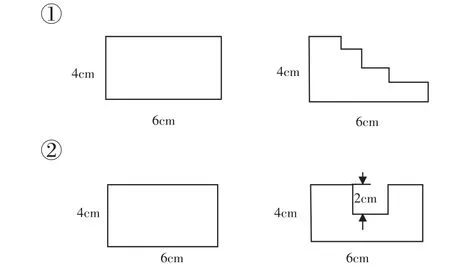
图4

师：同样是平移，为什么第①组的周长一样，第②组的周长不一样呢？

生5：因为通过平移后，第①组两个图形的周长都是长方形的周长，而第②组的第二个图形的周长比长方形的周长要多两个2cm。

B.下面图形中，甲和乙的周长谁更长？

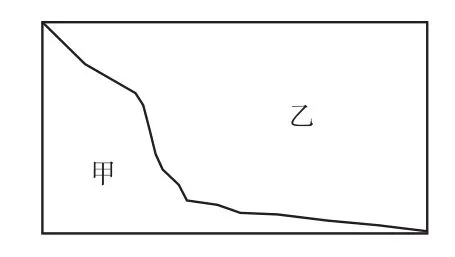
图5

师：你能找到甲和乙的周长吗？甲和乙的周长谁更长，你是怎么想的？

生6：甲和乙的周长完全一样，因为甲和乙的周长都是“长+宽+公共边”。

师：原来周长的长短与图形的大小无关，只与围成封闭图形的所有边的长度总和有关。因为封闭图形一周的长度就是周长。

C.有一块菜地，一面靠墙，其他面围上竹篱笆。竹篱笆长多少米？

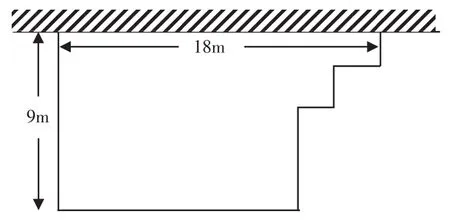
图6

相比教学片段2，教学片段3在细节上有如下变化：

教学从“单项思维”发展为“多向思维”。《论语》说：“举一隅不可以三隅反，则不复也。”长期以来，我们比较重视求同思维、归纳思维，但是现在的教学要求既要培养学生的求同思维，又要培养学生的求异思维、归纳思维、演绎思维、发散思维和逆向思维。只有这样，学生才能领会转化思想，从而对周长概念的理解更加深刻。

教学处理好了“过程”与“结果”的关系。课程改革十分重视“过程与方法”，并把它列为三维（知识与技能，过程与方法，情感态度与价值观）目标之一。在教学中，无论是探索新知，还是巩固练习，都应摆脱只传授“结果”和“结论”的弊端，处理好“结果”与“过程”的关系，这样的教学才是有价值的。教学片段2比较简单，重视了“结果”，忽略了“过程”，改进后的教学片段3的“过程”与“结果”和谐发展，既教给学生知识，培养学生能力，又渗透了数学思想，提高了学生的数学素养。

因此，教师的视界都可以开启学生的世界，唯有教师关注细节，教育的意义和人生的意义才能在师生视域融合中得以彰显。