车室声固耦合模态分析研究

， ，，

(1.许昌学院 电气机电工程学院，河南 许昌 461000;2.中国移动通信集团河南有限公司 许昌分公司，河南 许昌 461000)

我国汽车行业发展迅速，乘用车年销量在2000万辆以上，国产车在动力性和经济性提升显著，国内外品牌之间在此领域的差距逐渐缩小.但随着生活水平的提升，越来越多的消费者选车时考虑舒适性(NVH)的问题.而汽车的舒适性(NVH)恰恰是国内品牌与世界知名车企相比相对薄弱的.

车厢内噪声主要有结构的振动辐射传播噪声和空气传播噪声[1].车身振动对噪声影响很重要，车身的模态参数(模态频率和振型)反映车身的固有特性.车腔是以空气为介质，其同样具有模态频率和振型[2-5].声学模态频率是在某一频率声波下车腔空气产生共振，使声压突然增大；在某一频率声波在车室内传播时，声压不是由近及远的自然消减，而是入射波与入射波在室内壁板的反射波产生干涉，声波干涉造成了不同位置处声压叠加或消减.声学模态振型当车身的共振频率和车腔的共振频率相同时，车内共振位置处的声压会进一步提高[6-8].车内空腔声学模态频率和车身结构振动模频率多出现在20～200Hz范围内，故在低频区域内存在耦合的可能性较大，在随机激励下低频耦合模态响应过大将会对人体舒适性产生影响.因此，为了更好的控制汽车车室的噪声，分析车身、车室空腔的耦合模态是非常重要的[2].本文采用LMS公司的LMS Virtual Lab声学仿真软件，对国产某SUV进行声固耦合模态仿真分析.

1 模态分析基础

1.1 振动模态基本原理

白车身是一个多自由度系统，其动力学平衡方程表示.

(1)

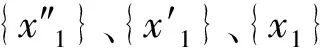
(2)

通过求解二阶线性齐次方程2，得到和模态参数有关的极值和留数.

1.2 声学模态分析基础

汽车乘坐室可以看做一个近似封闭的声学空腔，假设声腔内介质均匀，离散化处理后可得到空腔声学有限元模型，其微分方程同样可以用公式(2)改写.

[M2]{p″}+[C2]{p′}+[K2]{p}={F2}.

(3)

式中,{p}表示的是节点的声压矢量，{F2}为广义的力学矢量.通常情况下车身内饰壁板对于声腔模态参数的影响有限，在不考虑座椅的前提下，可忽略阻尼，3式同样可简化为

[M2]{p″}+[K2]{p}={F2}.

(4)

如果考虑车身振动对车腔声压的影响，车内空腔有限元方程为

[M2]{p″}+[K2]{p}+(ρ0c0)2[S]Tx2=0，

(5)

其中，ρ0为介质密度，c0是声波速度，[S]是结构—声学耦合矩阵，x是结构振动位移矢量.此时，白车身结构也会受到车腔介质振动的影响，通过耦合矩阵[S]作用在结构上.

白车身的有限元方程

(6)

式中{F}为施加在车身上的外力矢量.

2 汽车车身有限元分析

2.1 模型建立

首先建立车身的三维模型图，如图1所示.根据模态相似原则，在保持模型空间尺寸不变的前提下，对车身进行刚性化处理并同意车身板件厚度为4 mm(板件材料参数如表1所示)，忽略如结构中的倒角、螺栓等细节，最终建立了白车身整体简化模型，如图2所示.

图1 车身三维模型图

图2 车身整体简化有限元模型

具体参数如下.

表1 材料参数

2.2 有限元分析

利用LMS Virtual.lab中的Acoustics模块对整车有限元模型进行仿真分析，对汽车地板四个角施加全约束，对其在20～200 Hz频率范围内的模态参数进行仿真分析，表2列举了前十阶模态频率，图3和图4为一阶和二阶模态振型.

表2 车身前十阶模态频率(单位/Hz)

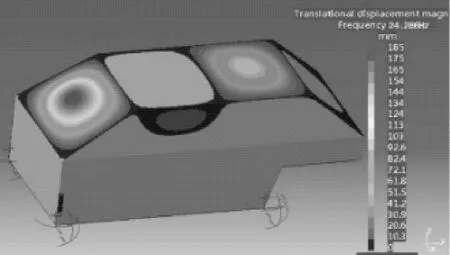
图3 一阶模态24.286 Hz

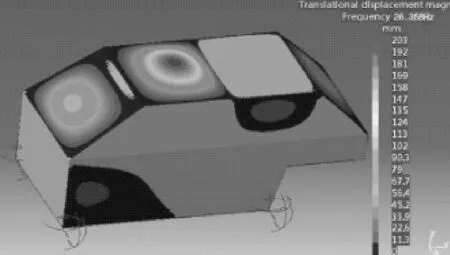
图4 二阶模态26.358 Hz

3 汽车声腔有限元分析

在简化的车身结构基础上，建立声腔模型，并假设声腔边缘的壁板为刚性壁板.考虑到座椅可能会对声腔模态产生影响，为了研究准确，分别建立的无座椅和有座椅两种声腔有限元模型.利用LMS Virtual Lab软件将模型进行网格划分，无座椅模型共包含10 688个节点，46 726个单元如图5所示；有座椅模型共包含12 788 个节点，47 126 个单元，如图6所示.

图5 无座椅车室空腔网格模型

图6 有座椅车室空腔网格模型

通过表3中对无座椅和有座椅模型的数据对比，两种模态皆沿纵向有一个节面，节面的位置略有不同，无座椅模型的模态频率比有座椅模态频率低20 Hz左右，模态振型整体趋势类似，但第三、四、六、七阶的模态振型也有不同，图7和8分别为有无座椅时第一阶模态振型，图9和10分别为无座和有座时的第三阶和第四阶模态振型.由此可见，座椅对车室空腔的模态参数有不可忽略的影响，因此后期的研究中，需要建立带有座椅的模型.

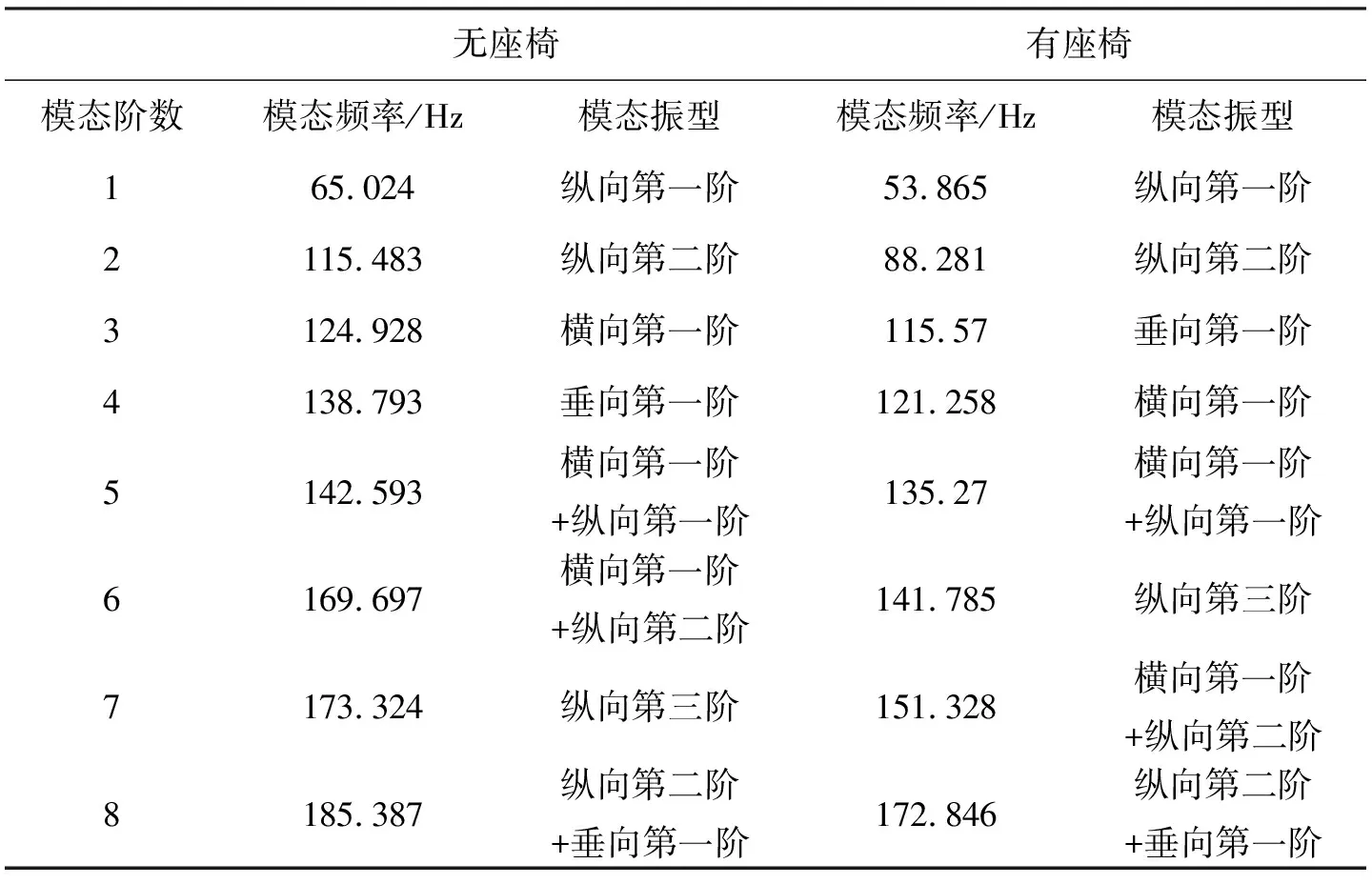
表3 有座椅与无座椅前八阶模态振型对比

图7 无座椅第一阶模态振型

图8 有座椅第一阶模态振型

图9 无座椅第三阶模态振型

图10 有座椅第四阶模态振型

4 声固耦合有限元分析

在LMS Virtual.Lab Acoustics模块中分别导入车身及声腔有限元模型，设置单元属性和网格类型，选定其边界条件，得到声固耦合的有限元模型，如图11所示.

图11 声固耦合模型

声固耦合模型是由结构模型和声腔模型组合而成，如图11所示，声固耦合模态由与车身的模态变形和与声腔模态的声压变形组成.这两个模态之间互有影响，空腔内的声压波动作用在车身壁板上可能引起局部变形，反过来，壁板的振动变形同样会引起车室空腔内介质的振动，进而引起声压的局部变化，声-固耦合系统的模态既与车身结构模态息息相关又受乘坐室空腔的声学模态的影响，通过模态分析和对比，如表4所示，声-固耦合模态一部分以车身的模态为主，也有一部分以车室的声学模态为主.下图12～15列举了声固耦合第一、二、五、六阶振型.

表4 声固耦合系统与车身结构的前六阶模态频率对比(单位/Hz)

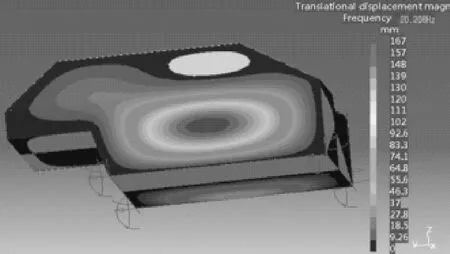
图12 第一阶声-固耦合模态振型

图13 第二阶声-固耦合模态振型

图14 第五阶声-固耦合模态振型

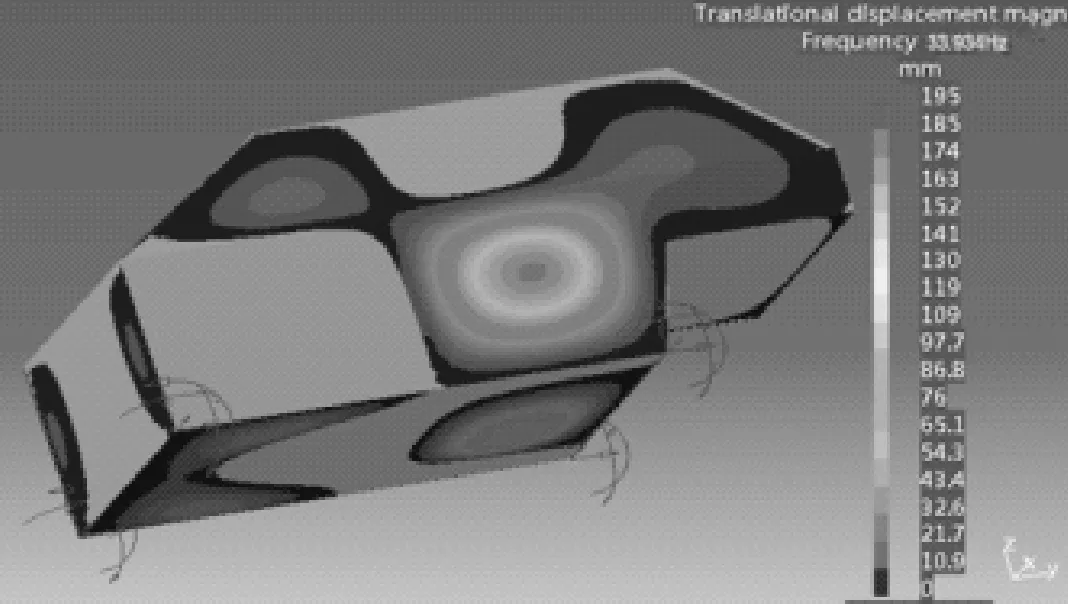
图15 第六阶声-固耦合模态振型

将车身与耦合系统的模态参数比较，低阶耦合模态以结构振动为主，其振型与车身的前十阶模态振型基本一致，而模态频率在声压波动的影响下有一定变化，但声腔内空气的阻抗较小，所以声学模态对耦合系统模态频率的影响较小.

车身结构模态与耦合模态类似的区域，其模态频率分布比较密集，到第69阶时耦合系统才出现以声学模态为主的情况，如图16所示.但是声-固耦合系统的模态还是以车身的结构振动模态为主，如图17所示，以声学模态为主的耦合模态振型与单独声学模态振型并不完全相同，节线的位置发生了一些改变，但模态频率相差较大.

图16 耦合模态第69阶模态振型

图17 声腔第一阶模态振型

5 结语

本文以某SUV为研究对象，通过建立车身模型并进行有限元分析，获取车身结构的模态参数；建立车身声腔模型并进行有限元分析，获得声腔的模态参数，并得出车内座椅对声腔模态的影响不可忽略的结论；在此基础上，通过声固耦合模型的建立，获得耦合状态下的模态参数，并使之与车身模态进行对比，由于耦合系统中车身与声腔的相互作用，使车身的模态参数发生了略微的变化，以车身形态为主的耦合模态在响应中占比较大.在车身及声腔设计过程中,调整车身结构以车室空腔形状将响应点位置移至远离人耳的位置或改变车身相应结构的刚度可以起到改善乘客体验的目的.