基于反向策略和柯西分布的粒子群优化算法
(内江师范学院 数学与信息科学学院,四川 内江 641112)
粒子群优化[1](PSO)是模拟鸟类捕食行为的仿生算法.该算法具有容易实现、收敛速度快等优点,在组合优化、聚类分析、神经网络训练等方面应用广泛.但该算法易陷入局部最优,所以诸多学者利用余弦函数的对称性对学习因子进行改进[2],或采用递减指数和迭代阈值[3]、自适应方法[4]、柯西分布[5]等对惯性权重进行改进,均促进了算法的发展.为加快算法的收敛速度和提高全局搜索性能,本文提出基于混沌和反向策略产生初始解,利用柯西密度函数和柯西分布函数对算法进行改进,通过4个经典函数进行测试,并与文献[2]、文献[6]进行对比,仿真结果表明:改进算法的收敛速度更快,搜索结果更有效.
1 粒子群优化算法
在D维搜索空间中,由m个粒子组成,第i个粒子表示空间向量xi=(xi1,xi2, …,xiD)(i=1,2, …,m),即第i个粒子在D维搜索空间中的位置是xi,其速度为vi=(vi1,vi2, …,viD).记第i个粒子搜索到最好的位置为Pi=(pi1,pi2, …,piD),整个群体搜索到最好的位置为Pg=(pg1,pg2, …,pgD).粒子的速度-位置方程描述为
(1)
(2)
其中,w是惯性权重,c1和c2为学习因子,c1是“自身认知”,是对自身信息的利用;c2是“社会认知”,是群体间信息共享;r1,r2为[0,1]中服从均匀分布的随机数.
2 基于反向策略和柯西分布的粒子群优化算法
2.1 基于混沌的反向策略机制
利用混沌运动的特点(初值的高度敏感性、遍历性、随机性)[7]进行初始化,可以使种群多样化,避免过于早熟.文章采取Logistic映射进行混沌初始化,其表达式为
Xn+1=μ·Xn·(1-Xn),n=0,1,2,…,N,
其中,0 反向学习[8]指在搜索过程中,同时考虑当前解和它的反向解,当前解有一半的概率比它的反向解更远离最优解,因此,采用基于当前解与反向解的精英选择策略来进行初始化. 综合以上改进,对改进办法进行实验:方法一,混沌与反向学习策略进行初始化;方法二,采用式(3)进行调整;方法三,采用式(4)对进行调整;改进算法,综合方法一、二、三进行调整. 对于上述方法,通过4个典型测试函数来测试: 采用MatlabR2010b,环境:CPU为Intel(R)Xeon(R) E5,2.6 Ghz,内存为8GB,操作系统为Windows7SP1. 分别对方法一、方法二、方法三以及标准PSO进行测试,各运行1 000次后取平均值及标准差,规定:惯性权重为0.5,学习因子都为2,粒子数为30,空间维数为30,结果见表1、2.由表1可知,方法一对单峰函数的寻优效果较好,对多峰函数表现一般;方法二对4个函数的寻优效果都有一定的提高;方法三在Sphere、Griewank的寻优中表现良好.由表2可知,三种方法对解的稳定性均有改进,说明该算法有效. 表1 各方法的最优平均值 表2 各方法下的最优值的方差 参数设置为:文献[6]中,c1,c2:1.5~2.5,w=1;文献[2]中采用余弦公式进行参数更新;本文的改进算法采用之前的设置值.实验结论如下:(1)针对单峰函数Sphere,改进算法每次都能找到最优值,但求解Rosenbrock时的改进算法弱于文献[6],优于文献[2];(2)针对多峰函数Rastrigin和Griewank,改进算法能够找到最优值(表3),优于文献[2]和文献[6];最优值的方差优于文献[2]和文献[6](表4),这说明算法更加稳定.综上所述,改进算法在收敛精度上有明显提高,能够避免陷入局部最优. 表3 不同粒子群优化算法的搜索结果比较 表4 测试函数的最优值的方差比较 针对算法易陷入局部最优的缺点,采用混沌和反向策略产生初始解,能使算法更好地覆盖解空间,产生较好的初始解;利用柯西密度函数对惯性权重进行调整,利用柯西分布函数对位置更新公式进行调整,通过实验来验证三种调整方法的有效性.改进算法在寻优中表现更好,特别是在多峰函数中.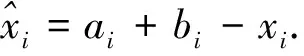
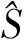
2.2 基于柯西密度函数的惯性权重调整
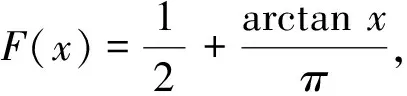
2.3 基于柯西分布函数的粒子位置更新
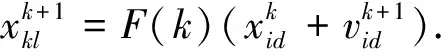
3 实验结果与分析
3.1 测试函数与配置
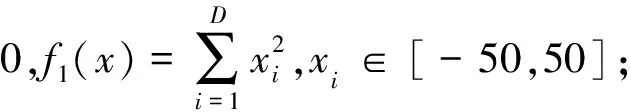

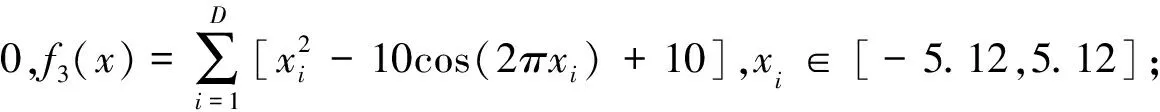
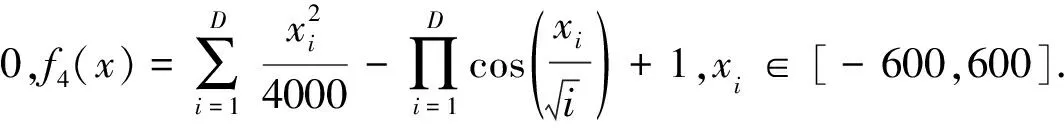
3.2 改进方法的有效性测试


3.3 改进算法的比较实验


4 结语

