为什么圆锥的体积是Sh

◇邱月亮

如图1，我们把一个底面半径为R、高为H的圆锥，以平行于底面的截面，按高度把它平均分成n份。我们分的份数越多，其中的每一份就越能近似地看成一个小圆柱。我们不妨从上往下数，讨论第i个小圆柱，显然它的高为，并设其底面半径为r，则它的体积为。从图1中可以看出，其中的r与R、h和H存在着这样的关系：即而所以因此，第 i个小圆柱的体积为

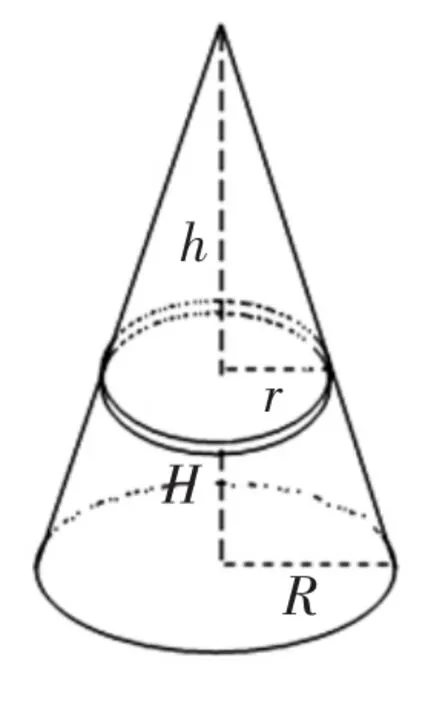
图1

把这n个小圆柱的体积全部相加，并设它们的和为V，即

不难发现，当分的份数越多，即n越大时，V越接近圆锥的体积。也就是当n→∞时从而，即就是圆锥的体积。

仔细分析上述过程，它实质上是一个“先细分，再求和”的过程，即先把圆锥分成若干个细小的部分，然后对这些细小部分的体积进行求和。其实这是定积分思想的雏形，这种思想对于小学高年级的学生来说，不但能发现，而且能掌握和运用 （可参看贵刊2016年第6期笔者的 《先细分，再求和》一文）。

现代小学数学教学，已经不再完全用静态的观点来让学生认识几何形体，而是以变化的、联系的观点来认识其中的点、线、面和体。圆柱可以认为是以长方形某条边所在的直线为轴旋转而得，同样地，圆锥也可以认为是以直角三角形某直角边所在的直线为轴旋转而得。显然，这种以某个平面图形为母体旋转所得到的旋转体，其体积的大小与母体面积的大小有关。但是，为什么面积关系是1∶2的等底等高直角三角形和长方形，它们分别旋转后所得到的圆锥和圆柱的体积关系却是1∶3呢？如图2。

图2

其实，我们不难发现，在“制造”旋转体的过程中，母体平面图形中的每一点，处在与中心轴垂直的平面上，作与中心轴之间保持距离不变的运动，从而“繁衍”出一些新的点，而这些新生成的点，构成了一个个新的圆。由母体中的全部点所生成的这无数多个大小不一的圆，也就构成了旋转体。显然，这些新圆的大小影响着旋转体体积的大小。如图2中，直角三角形右下锐角的顶点，在旋转的过程中，它处于与中心轴垂直的平面上，并始终与中心轴保持着r的距离，从而“制造”了圆锥底面的边界；同样地，其另一个锐角的顶点，在某个位置与中心轴始终保持着0距离，所以也就“制造”了圆锥的顶点。

在母体那么多的点中，由于它们与中心轴之间的距离各不相同，所以我们很难当然也不可能把它们的大小都表示出来，只能选择其中的一个作为代表来反映其与旋转体体积的关系。根据物理学中的有关知识，最能体现一个平面的本质属性的点，即为其重心所在的点。因此，从图2可以看出，长方形重心所在的点为两对角线的交点，它在旋转过程中距中心轴的距离为r；三角形重心为三条中线的交点，它在旋转过程中距中心轴的距离为

根据古尔丁定理，旋转体的体积等于母体平面图形的面积与其重心所在的点旋转时所形成的圆的周长的积。由此我们可以得出：由长方形旋转所得圆柱的体积是由与长方形等底等高的直角三角形旋转所得圆锥的体积是