自回归模型参数和的置信区间估计
彭毳鑫,殷珍妮,赵志文
(吉林师范大学a.大学外语部;b.数学学院,吉林 四平 136000)
0 引言
考虑自回归模型:

其 中 Yr(t-1)= (Yt-1, Yt-2,…,Yt-p)τ, α(r)=(α1,…,αr)τ为未知参数向量,{εt}为独立同分布的随机变量序列,满足E(εt)=0,E)=σ2。
自回归模型是一个重要的时间序列模型,在实际中被广泛应用于各种时间序列观测数据的建模分析[1-3]。对于自回归模型的统计推断,陈敏与吴国富在延迟参数、门限以及模型阶数给定的情况下,讨论了门限自回归模型残差方差以及模型参数的最小二乘估计的强收敛速度[4];林正华和冯仁忠利用约束规划及计算数学理论,讨论了自回归模型参数的精确估计方法[5];王黎明分别讨论了模型白噪声序列的方差已知和未知情形下一阶自回归模型参数的AbruptChange-Point和GradualChange-Point的检测问题[6];金阳和安鸿志讨论了非线性自回归模型的平稳解边际尾概率与扰动项尾概率之间的关系,在模型满足平稳遍历性的条件下,证明了一维平稳解边际分布的重尾概率指标与扰动项指标相同[7];赵志文和王德辉研究了广义随机系数自回归模型中参数的估计问题,获得了一个估计类中的最小渐近方差估计[8]。Chambers研究了平稳自回归模型的Jackknife估计问题,证明了当误差非正态时Jackknife估计优于普通的最小二乘估计[9]。Chambers和Kyriacou研究了单位根自回归模型的Jackknife估计,证明了Jackknife估计没有充分地估计一阶偏差[10];Chen和Yu则进一步讨论了单位根模型的最优Jackknife估计问题[11]。
本文在上述研究基础上,进一步讨论模型参数的估计问题。给出了模型参数和的估计,证明了该估计量的极限分布为正态分布,同时对极限分布的渐近方差进行估计。也给出了模型参数和的置信区间估计,该结果可以用于检验观测数据为白噪声序列还是自回归序列。
1 方法和主要结果
给出模型(1)中未知参数和的估计方法。
参数 β 的估计。基于观测数据 (Y1-γ, Y2-γ,…,Yn),利用最小二乘法,考虑最小化关于α(r)的函数:

对Q关于α(γ)求导,建立关于α(γ)的估计方程:

进而可以获得α(r)的估计:

由α(r)的估计进一步可以获得β的估计:


定理1:若假设条件A1和A2成立,则:
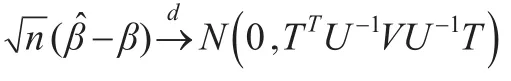
考虑定理1中渐近方差V的估计。为了估计V,首先考虑未知参数α(r)的估计。本文仍采用α(r)的最小二乘估计̂(r)作为 α(r)的估计。在此基础上,进一步考虑 V的估计̂。令:

定理2:若假定条件A1-A2成立,则:

定理3:若假定条件A1-A2成立,则:

定理4:若假定条件A1-A2成立,则:
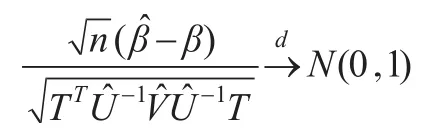
基于定理4,可以构造未知参数β的置信区间。对于给定的置信水平0<δ<1,令ξδ满足
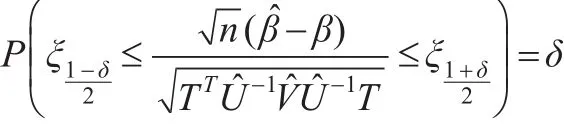
dx=δ,可知:进而可知未知参数β的置信区间为:

2 模拟
对于模型(1),在不同的模型阶数、模型参数、样本量以及置信水平下计算模型参数和的置信区间的覆盖率。对于模型阶数r,分别模拟了r=1、r=2、r=3以及r=4四种情形,对于每一种情形,本文选取不同的模型参数真值。样本量n分别取为50、100与300,置信水平取为0.90以及0.95。模拟结果由表1给出。
由表1中的模拟结果可以看出,无论置信水平取为0.90还是0.95,随着样本量的增加,本文所构造的置信区间的覆盖率更接近真实的置信水平。并且对于不同的模型阶数和模型参数以及不同的样本量,本文所构造出来的置信区间同样具有较好的覆盖率,这说明本文的方法具有一定的稳健性。
3 定理的证明
3.1 定理1的证明:
注意到:

表1 置信区间的覆盖率

由条件A1和遍历性定理知:

接下来证明:
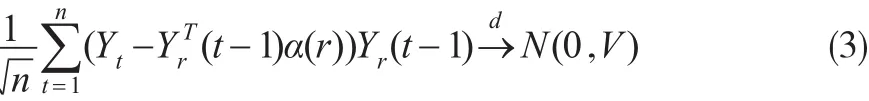

令:
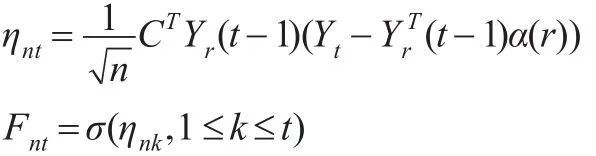

显然式(8)成立,下面证明式(5)。对于∀ε>0,
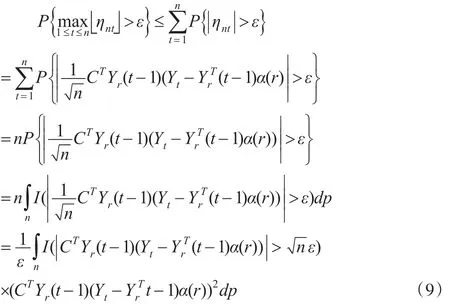
对于式(6),由遍历性定理可知:

最后证明式(7)。注意到:
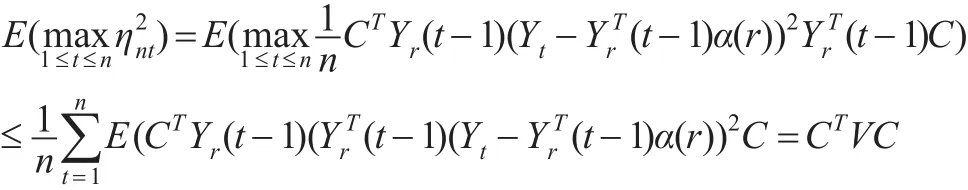
由此证明了定理1。
3.2 定理2的证明
注意到:

由遍历性定理易知:

下面考虑Hn2。注意到:
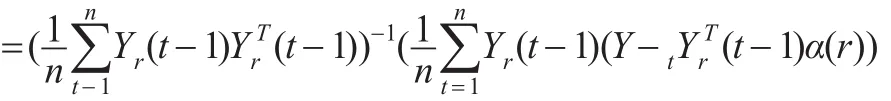
由遍历性定理易知:

此外,注意到:

由此可知:

进而有:

由遍历性定理知以及式(10)易知:
同理可证:

综合式(10)、式(12)以及式(13)可知定理2成立。
4 总结
本文给出了自回归模型参数和的估计方法,同时讨论了估计量的极限性质,证明了该估计量具有相合性,并且其极限分布为正态分布。基于该估计,可以构造自回归模型参数和的渐近置信区间,给出参数和的区间估计。本文也对上述的理论研究结果给出了数值模拟分析,模拟结果表明本文所提出的的方法在实际中具有可行性。此外,该方法也可以用于检验模型的参数是否为0,进而对模型定阶,这在实际的建模分析中具有重要的统计意义。

