三参数Weibull分布有限混合模型及应用

刘福香

（哈尔滨商业大学 经济学院，哈尔滨 150028）

0 引言

有限混合模型（Finite mixture models,FMM）是利用有限个已知分布的混合去拟合数据分布的参数方法。主要用于表现数据的分布及变异程度，特别擅长拟合数据是多峰、有偏和结尾等数据类型。FMM也可以用于频数数据或分组数据的分布结构探索，即也可以用于分类研究，并估计每一类别的比例。本文通过介绍FMM的原理及实际应用，并与现在通用的研究方法比较，为研究者提供借鉴。

1 有限混合分布模型介绍

有限混合模型（FMM）又称为有限混合分布模型，它是有限个已知分布的混合。现在主要应用于经济、渔业、生物、医药等领域[1-3]。FMM可以估计每个已知分布函数的参数，还能估计出每个组成部分的比例[4]。FMM模型可以拟合不同分布函数的混合，例如Γ分布、正态分布、β分布、logistic分布、正态分布、Weibull分布[5]。参数估计方法有矩估计[6]、极大似然估计、Bayes估计[7]等。

1.1FMM模型原理

假设有k个分布函数混合（j=1,2,…,k），x是目标随机变量，例如本文中的树的胸径。fj（x）是对应第j个组成分布的概率密度函数，f（x,p）就是对应的有限混合模型，有限混合函数表示为:

其中 p=（p1，p2，…，pk-1）是 k-1 个组成部分的比例向量。每个独立成分必须满足下面的限制条件：0＜pj＜1和其中，f（x,p）可以是同一分布函数，也可以是不同分布函数的混合。

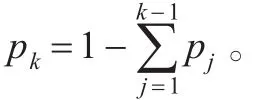
在本文中，以3个参数的Weibull函数的混合为例，fj（x）:

其中aj，bj和cj分别是对应第j个组成成分的位置参数、尺度参数和形状参数。

第j个组成成分的累计概率密度函数为：

因此，有限混合对应的累计概率密度函数为：

1.2FMM模型参数的估计

在本文中，模型的参数估计采用极大似然估计，因为极大似然估计具有均方误差较小及相合性等比较好的统计特性。

FMM对应的似然密度函数为：

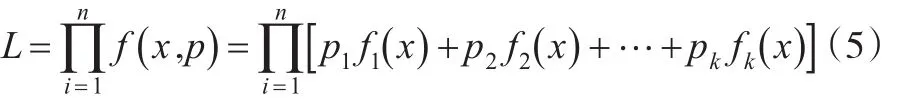
对似然函数取对数，如下：

然后对式（6）的对数似然函数求偏导，找到使得函数取得最大值的对应参数值，即偏导数为0，最后可以利用迭代法求出参数的值。

FMM模型是基于数据分类的比较有效的方法，但是对于数据中具体分成多少个成分，目前是研究界的问题之一，本文也涉及这一问题的讨论。本文在以天然的混交林中已知树种组成的前提下，利用FMM模型拟合实际林分的直径分布，与普通的方法比较。探讨FMM模型应用优势及劣势。

2 数据来源及模型应用

本文以两个三参数的参数Weibull分布函数进行混合，来拟合天然混交林分中各个树种的径阶分布,分别与全林分用一个Weibull分布函数的拟合，与每个树种分别用一个Weibull分布函数的拟合，并于FMM模型相比较。利用统计软件SAS9.3中的FMM Procedure过程进行数据整理和处理。

2.1 数据来源及整理

本文数据用的是大兴安岭地区，位于西林吉林业局、图强林业局和阿木尔林业局的天然混交林的四块样地的直径分布数据，分别记为1号样地、2号样地、3号样地和4号样地。其中1号样地是落叶松-白桦两个树种的混交林，3号样地和4号样地是落叶松-白桦-蒙古栎3个树种的混交林。分别对这四块样地进行径阶整理分组，以2为径阶矩，再对每个径阶的株数进行汇总，并对树种进行分类。表1是对数据的描述性汇总。4直径分布柱态图如图1所示。

表1 描述性统计

图1 4直径分布柱状图

2.2 模型应用

对应的分布函数如下：

其中i表示第i径阶，其中共s个径阶，xi是第i个径阶对应的中值。p1对应第一个树种的比例，即p1=N1/N，也就是这一树种占整个树种的比例，N1，N2林分中两树种对应的株树，p2同上。

因此，式（7）可以被改写为：

拟合林分直径采用以下三种方法并进行比较：

方法1：FMM模型方法，即三参数Weibull分布的混合；

方法2：用一个三参数Weibull分布函数模拟整个样地的直径分布形态，不分树种。

方法3：分树种进行分别拟合，然后再加总，得到整个样地的拟合情况。

最后比较三种方法拟合优劣。

2.3 模型评价指标

模型评价指标包括AIC信息准则 （AIC）、偏差（Bias）、均方 根 误差 （RMSE）和似然 比 χ2检 验 （likelihood-ratio χ2test），如下：

其中logL是对应模型的对数似然函数，m是有效的参数数量，AIC越小越好。

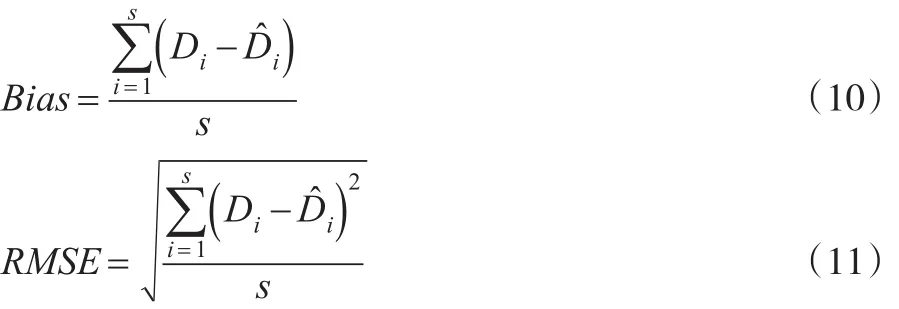
其中s是径级的数，Di是第i个径级的直径的和，̂是模型估计的第i个径级的直径的和。第i个径级的直径的和其中Ni是第i个径级的株数，di是第i个径级中值。

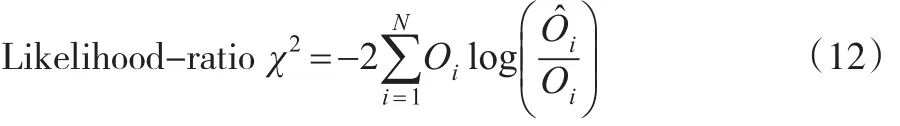
其中Oi是第i个径级观察株数是第i个径级有模型预测的株数。 χ2检验的自由度是（N-m-1），m被估计参数的数量。

本文中，模型的残差是：

这个残差的优势是可以给较大径阶的树木有较大的权重，因为在实际的林业经营中较大径阶的树木有较大的经济效益。给它赋予较大的权重，有利于林业经营管理。

3 模拟结果及讨论

对整块样地的拟合看出方法1（FMM）明显优于方法2和方法3，方法1的平均偏差、均方根误差和似然比卡方值都明显优于方法2和方法3（见表2）。而且方法1考虑了每个树种的组成比例。样地1和样地2直径分布属于反J型分布，样地3和样地4属于双峰分布，方法1都体现了很好的拟合效果，方法2对于拟合样地1和样地2也体现了较好的形式，只有方法3效果不佳，说明不考虑树种分别拟合是不符合实际的。在预测方面方法2和方法3都高估了实际株树。特别是在18cm径级和26cm径阶有小幅的波动，方法2和方法3都没有表现出来。对于三个树种的混合（样地3和样地4），模型1（FMM）也表现了比较好的拟合效果。

对于树种比例的预测，只有方法1（FMM）和方法3能对比例进行预测，方法2是对整块样地直径分布进行拟合，所以表3比较了方法1（FMM）和方法3对树种比例的预测结果。样地1和样地2，方法1（FMM）也优于方法3，样地3和样地4，方法1（FMM）与方法3各有优劣（见表3）。由于样地3和样地4是三个树种的混合，其中蒙古栎在林分中的比例较少，也影响了比例的估计，如果对于样本数量增加会提高估计的效果。3种方法对4块样的拟合结果见图2，其株数预测残差图见图3。

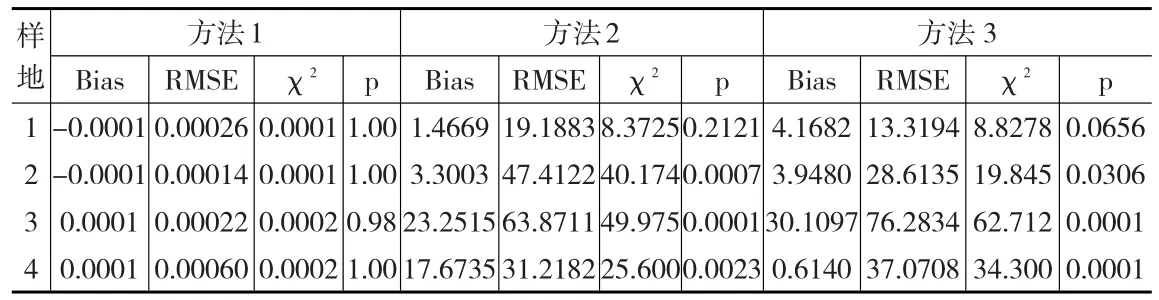
表2 三种方法的Bias、RMSE和χ2检验结果

表3 方法1和方法3对树种比例的估计

图3 3种方法对4块样地的株数预测残差图

4 结论

本文研究了三参数Weibull分布函数的FMM模型的应用，拟合了混交林直径的分布，拟合结果表明三参数Weibull分布函数的FMM模型能够灵活地表现数据的特征，并能对每个组成部分的比例进行估计，并与传统的方法进行比较，得到了理想的结果。核密度估计方法也可以用于描述数据的分布形态，但是它对未知分布的描述也不是最准确的，相比FMM模型有一定的优势，在以后的研究中可以进行比较。FMM模型也可以用于聚类分析，并且能够估计每一类的比例，且考虑数据中未被考虑到的异质性。