公转速度对冷滚打成形制件回弹影响研究

崔莅沐 肖继明

(西安理工大学机械与精密仪器工程学院，西安 710048)

0 引言

冷滚打成形是一种利用金属材料自身塑性，通过滚打作用的累积效应，成形高性能齿形制件的无模无约束自由塑性成形技术[1-2]。与传统基于模具的成形工艺相比较，冷滚打成形技术不仅可以提高效率、降低成本、节约材料、降低污染，也展现出了能耗低、载荷小、柔性高等特点，逐渐引起了国内外诸多学者的关注[3-4]。

在冷滚打成形过程中，随着滚打轮对工件的高速击打和滚压，成形区域金属材料的非线性变形会使得工件的变形区域储存了很大的弹性应变能。滚打成形结束后，随着工件成形区域所受的接触压力的消除，储存的弹性应变能逐渐释放，会使已变形区域出现逆向变形，产生回弹现象[5]。回弹量的大小对最终制件的几何精度有着显著影响，因此控制回弹从而获得高精度的成形工件成为冷滚打成形中的关键因素。

起初的回弹研究主要是在一些简单零件纯弯曲或者拉弯成形中，大多数采用解析法[6]；70年代之后有限元数值分析的方法在回弹的研究中得到越来越广泛的应用，W. JOHNSON[7]使用有限元仿真的方法模拟了梁的回弹，F.MICARI[8]研究了三维板料成形中的回弹现象等；M.HUANG[9]等总结了关于回弹模拟的研究进展，近些年来通过数值模拟很好地解决了回弹研究中的诸多问题，但是对于冷滚打成形中的回弹现象，目前还尚未进行系统的研究。

在冷滚打成形过程中，影响弹性应变能的主要因素有打入量、滚打密度和公转速度等，这些因素相互作用使得冷滚打成形中的回弹变得很复杂[10]。传统的有限元动力显式算法计算回弹问题[11]，由于计算结果不够准确，而需要与隐式算法模拟相结合进行计算[12]。本文对冷滚打成形工件中变形部分的回弹量进行数值模拟，研究了公转速度对回弹的影响规律，在冷滚打成形设备上进行了实验验证，为冷滚打的精密成形提供了参考。

1 冷滚打成形原理

冷滚打成形是一个高速、瞬态、强冲击、大变形的复杂成形过程。是利用金属固有的塑性，使用特定廓形、高速旋转的滚打轮对工件进行逐点断续滚压和打击，使工件表层金属产生塑性流动，利用滚打轮与工件之间的相对运动关系产生累积效应，最终形成预定形状要求的一种无模无约束自由塑性成形技术[13]。块体材料冷滚打成形原理如图1所示，滚打轴上偏心安装具有特定廓形的滚打；滚打轴旋转时带动滚打轮绕滚打轴中心公转，随着滚打轮与工件位置的变化，滚打轮对工件表面产生击打、滚压而产生了塑性变形[14]， 同时在摩擦力作用下滚打轮产生了自转，减小了摩擦。

图1 块体材料高速冷滚打成形原理Fig.1 Principle diagram of cold roll-beating forming

2 动态仿真

冷滚打成形过程是一个非线性程度极强的复杂问题，若采用隐式算法模拟冷滚打成形过程，在迭代计算过程中，程序需要判断滚打轮和工件直接的接触关系，会造成计算效率低，且容易导致计算结果的不收敛。而动态显示算法的稳定性较好，且计算速度较快，一般不存在收敛性问题[15]。

2.1 动态显式仿真模型建立

2.1.1几何模型和材料模型

冷滚打成形过程中是一个动态冲击、局部加载和卸载的周期变化过程，同时涉及高应变率和大应变问题，所以选择比较适合的J-C模型进行仿真，模型参数如表1所示。为了减小计算时间，将冷滚打成形时的复杂模型进行适当简化，其几何模型和装配的参数如表2所示。在ABAQUS/CAE中建立仿真模型如图2所示，其中滚打轮材料为解析性刚体。

表1 J-C模型参数Tab.1 J-C model parameters

表2 几何模型参数Tab.2 Parameters of geometric model mm

图2 冷滚打成形有限元模型图Fig. 2 Finite element model of cold roll-beating forming

2.1.2单元选择及网格划分

本次仿真中工件采用的是三维实体单元，在仿真中网格会扭曲变形，但线性减缩积分比完全积分积分点要少，减少了计算时间，且扭曲变形时对精度影响不大，所以网格单元类型选择C3D8R。对工件进行分块划分网格，单元个数为478 080个，具体如图3所示，细化部分网格单元边长为0.1 mm，粗化网格边长为0.5 mm，滚打轮材料为解析刚体。

图3 划分网格后的工件Fig.3 Gridding model of blank

2.2 动态仿真结果分析

2.2.1成形过程变形力仿真分析

选用40Cr 作为工件材料，给定滚打深度为0.3 mm，对不同公转速度下的滚打成形进行数值模拟，获得Mises力分布如图4所示。可以看出，随公转速度增加，材料变形速度增加，Mises力的最大值先增大后减小。当公转速度从1 200 r/min增加到1 800 r/min时，Mises力的最大值从1.282 GPa增加到1.423 GPa，公转速度继续增加到2 200 r/min时，Mises力的最大值逐渐减小到1.390 GPa。

图4 不同公转速度下Mises力的动态仿真云图Fig.4 Dynamic simulation of mises stress distribution in different rotational speed

冷滚打成形过程中，金属材料在高应变速率下产生变形，其中流动应力增大产生硬化，塑性变形能转化成的热量引起软化，因此在变形部分的材料存在软化和硬化交互作用。当公转速度从1 200～1 800 r/min时，加工硬化作用大于软化作用，变形抗力增加，Mises力增加；当公转速度超过1 800 r/min时，软化作用大于硬化作用，变形抗力减小，Mises力减小。

2.2.2成形工件变形仿真分析

选取打入量最大时的截面为参考面，建立分析路径如图5所示，分析不同公转速度下成形工件在x(切向)、y(轴向)和z(径向)三个方向的变形规律。根据截面齿槽各部分不同的变形情况划分四个变形区域，如图6中所示，其中I为齿槽底部区域；II为齿槽倒角区域；III为齿壁区域，IV为齿顶区域。

图5 路径选取 Fig.5 Path selection

成形工件上材料在径向(z向)变形最终形成齿槽，同一路径下不同公转速时的成形齿槽截面如图7所示，齿槽轮廓形状基本相近，个别区域的变形趋势存在一定的差异，为了更清楚了解z方向变形随公转速度的变化规律，对图7中局部区域进行放大，如图8所示，公转速度为1 200～1 600 r/min时径向深度变化比较小，公转速度从1 800～2 200 r/min时z方向变形量逐渐增加；从齿槽底中心到倒角之间，差异逐渐减小，最终在倒角处(II区域)廓形基本重合；从倒角开始到齿顶之间(III区域)，z方向变形先增大后减小，公转速度为1 800 r/min时廓形齿壁最靠近滚打轮截面；从齿顶(IV区域)到边界处的变形，随公转速度增加而变小。

图6 齿槽截面变形区域划分Fig.6 Deformation area of tooth slot section

图7 不同公转速度下z方向变形Fig.7 Deformation under different rotational speeds in the z direction

图8 z方向变形局部放大图Fig.8 Local enlarging graphs in the z direction

齿底部分沿z方向的变形主要由滚打轮的滚压产生，齿壁部分主要由滚打轮侧壁的挤压和摩擦产生，齿顶到制件边界之间的变形主要齿顶变形部分影响产生。当公转速度增加时，与滚打轮接触的各部分的变形不但受材料的软化和硬化交互作用，同时也受到惯性力的影响。滚打速度在1 200～1 600 r/min时，滚打轮对工件的反复击打产生加工硬化，槽底部的材料变形困难，因此该阶段变形量变化不大；当滚打轮转速达到1 800 r/min时，变形部分材料由于温度升高软化起主要作用，所以变形相对容易，变形抗力减小，此时惯性力主要体现在卸载后材料继续产生少许变形，公转速度越高，齿槽底部变形深度越大；齿壁距离齿顶比较近，齿壁金属在滚打轮侧壁挤压和摩擦下可以向齿顶流动，形成凸起，当公转速度从1 200 r/min增加到1 800 r/min时，齿壁路径上材料变形速度增加，金属温度将升高，降低了变形抗力，塑性增加了，变形增加，当公转速度超过1 800 r/min时金属变形抗力增加，塑性降低，所以变形减小；当公转速度1 200 r/min增加到2 200 r/min时，齿顶到边界路径上材料受已变形区域的影响逐渐减小，当公转速度增加时，滚打轮与制件接触时间变短，变形区域对附近材料的影响减小，所以制件齿顶到边界之间在z方向的变形减小。

随公转速度增加，路径中间部分(I区域)点在x方向的变形先增加后减小，且变形方向与滚打轮公转方向一致(x正方向)，在该方向的变形力主要是滚打轮与工件之间的摩擦力。如图9(a)所示，冷滚打成形中，当公转速度增加时，x方向材料变形速度增加，金属温度将升高，降低了变形抗力，塑性增加，变形增加，当公转速度超过1 800 r/min时，金属变形抗力增加，塑性降低，所以变形又减小了。

公转速度增加时，路径上材料在y方向的变形增加，在y方向呈近似正弦曲线变化，且有逐渐减小趋势，中心点在2.5 mm处，如图9(b)所示，在冷滚打成形过程中，齿槽底部金属主要沿着滚打轮截面向两边流动，滚打轮两侧y方向的变形力在中心点处相互抵消，因此该位置沿y方向的变形量为零；从中心点向外，发生变形时受到的约束力逐渐减小，金属材料越容易变形，y方向变形量的最大值出现在倒角处；倒角处到齿顶部位，金属主要是形成轮截面的凸起，y方向的金属变形又逐渐减小。对照图6可以看出， I区域到II区域的变形量随着公转速度的增加逐渐增大，峰值出现在公转速度为1 800 r/min时，当公转速度超过1 800 r/min时，y方向的变形量逐渐减小，原因与路径上材料在x方向变形类似。

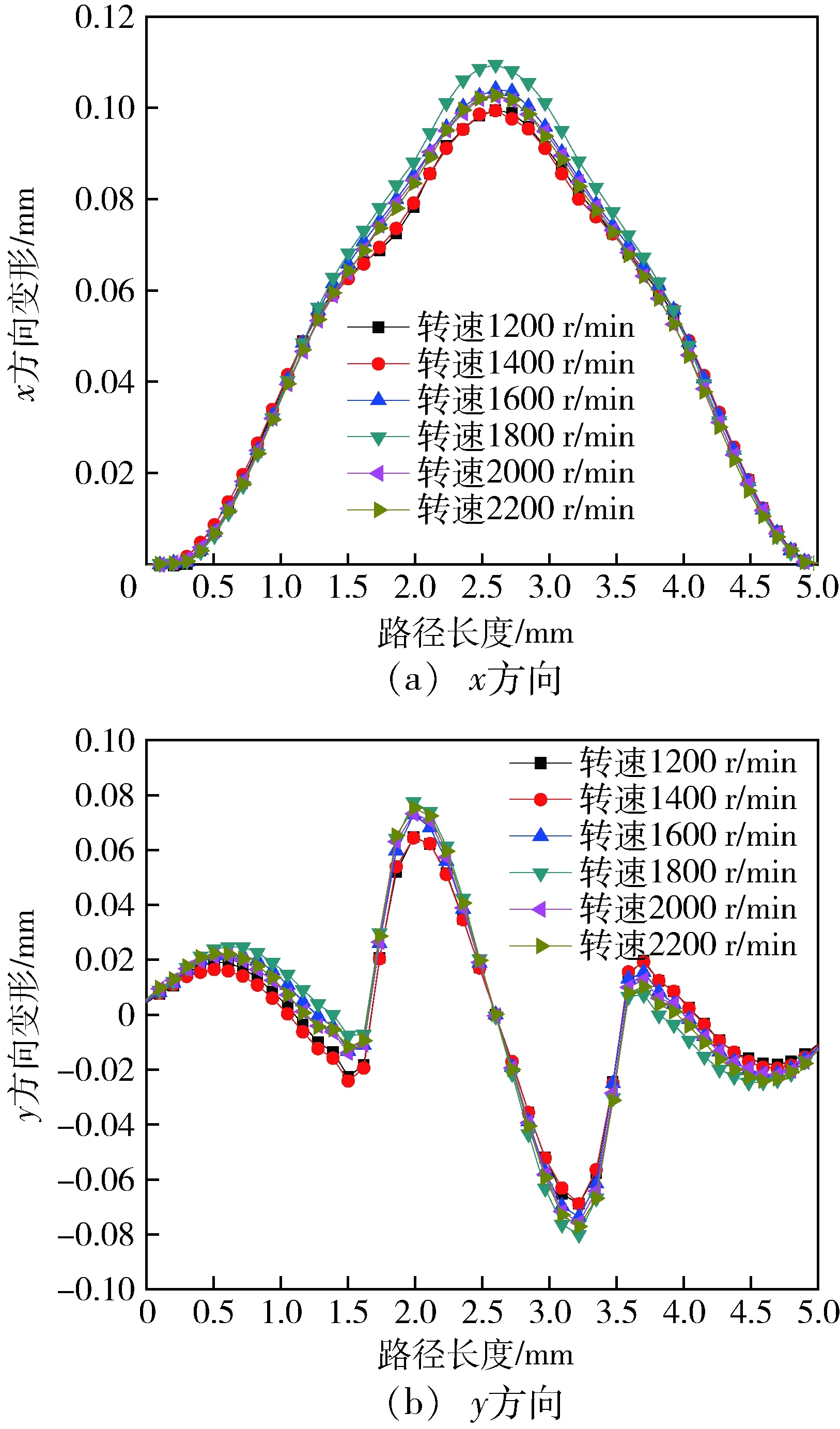
图9 不同公转速度下x，y方向的变形Fig.9 Deformation under different rotational speeds in the x and y direction

为进一步研究不同公转速度下滚打成形工件的回弹规律，并获得到较为准确的计算结果，把冷滚打动态仿真的结果导入到静态分析的有限元模型中继续分析。

3 动态结果的静态仿真与分析

3.1 建立静态隐式仿真模型

将在ABAQUS/EXplicit中计算完毕的结果导入到ABAQUS/Standard中，建立静态求解模型，从而来求解回弹。静态求解的源程序中设置：STATE=YES，输入模型的应力状态；UPDATE=YES，输入模型的应变状态；nlgeom=YES，增量步数inc=10 000，静态仿真模型如图10所示。

图10 静态处理工件模型Fig.10 Static model

3.2 静态隐式仿真结果分析

通过静态处理获得处于平衡状态的工件内部力Mises力云图，如图11所示，随着公转速度增加，Mises力由975.1 MPa先减小至972.9 MPa后增大993.6 MPa，转折点在1 800 r/min附近， Mises力的最大值基本都分布在齿槽底部。

图11 不同公转速度静态处理后Mises力云图Fig.11 Dynamic simulation of Mises stress distribution in different rotational speed

在静态仿真中材料发生的变形即为回弹，不同公转速度下各方向的回弹量见图12。z向的回弹如图12(a)所示，从齿底中间部位到齿顶之间，路径上点在z方向变形回弹逐渐减小，且齿底与齿顶回弹方向不同；回弹量随着公转速度的增加先减小后增大，最小值出现在公转速度为1 800 r/min时，此时主要是变形区域的温度升高出现软化现象，使得金属材料塑性提高，因此成形工件内部储存的能量较少，回弹变形量也最小。

路径上材料在x方向的回弹与变形方向相反(x正方向)，随着公转速度的增加，从齿顶到制件边界之间路径上材料的回弹规律基本相同，回弹量减小。齿槽底部中点到齿顶之间路径上材料的回弹量有减小趋势，但规律性并不明显，且波动比较大，如图12(b)所示。齿槽底部中点到齿顶之间路径上材料在滚打轮摩擦作用下产生切向变形，随公转速度增加，变形部分材料温度快速升高，当滚打轮离开时，高温材料降温较快，回弹量随之降低。

静态分析过程中，随着公转速度的增大，路径上材料在y方向的变形增加，但回弹现象不明显，具体如图12(c)所示。在冷滚打成形过程中，y方向的变形主要出现在齿槽底部的倒角部位，且在变形的同时累积了较多弹性应变能，当载荷卸除时，成形时储存的弹性应变能逐渐释放，因此回弹现象较为显著；且由于倒角处特殊的结构，能量只能沿着齿壁向外释放，所以成形后的工件会继续变形，因此冷滚打成形的齿槽廓形会大于滚打轮截面形状。

4 实验验证

在由卧式铣床改造的冷滚打机床进行实验，如图13所示，滚打轮安装在自主设计的滚打头的偏心夹具上，工件装夹在水平工作台上，主轴的带动滚打轮击打、滚压工件实现冷滚打成形运动。制件材料选用40 Cr，工件尺寸为120 mm60 mm20 mm，进给速度为1 mm/s，打入深度设置为0.5 mm，选取公转速度为1 200 、1 800 r/min进行滚打实验，成形工件如图14所示。

图13 冷滚打机床 Fig.13 Rack cold roll-beating machine

图14 工件廓形图Fig.14 Photo of workpiece

通过VHX-2000C超景深三维显微系统对成形工件的廓形进行测量，如图15所示。将实验所得的廓形与仿真结果以及滚打轮的廓形进行对比[图16(a)(b)]，与滚打轮截面对比，整体齿廓基本一致；对比可以发现，公转速度为1 800 r/min时成形材料的塑性较好，且回弹量较小。在齿壁和齿顶部分，实验所得廓形略大仿真结果，这是因为仿真所得廓形为完全回弹后的形状，而实验所测的工件廓形是弹性应变能未完全释放情况下的形状，所以实验得到的廓形略大于仿真结果。

图15 齿廓测量装置Fig.15 Tooth profile measurement device

图16 廓形截面图Fig.16 Profile section

5 结论

(1)动态仿真了冷滚打成形工件廓形随滚打轮公转速度增大时的变化规律：在x、y和z方向变形量均增加，其中y方向的变形呈近正弦变化，z方向齿槽两边的凸起增加。

(2)通过静态分析获得路径上不同方向随公转速度增加时的回弹规律：路径上点在x方向的回弹量增加，与变形方向相反，在y方向的变形增加时，回弹现象不明显；随着公转速度增加，z方向的回弹量逐渐减小，且从齿底中间部位到齿顶之间，呈现先减小后增大的趋势。在公转速度1 800 r/min时，材料软化作用起主导作用，路径上材料的塑性最好，变形后制件内部储存的能量最少，回弹变形量最小。

(3)在改装的冷滚打成形设备进行了实验，获得了齿槽的廓形截面，与相同工艺条件下的仿真结果进行比较，廓形基本吻合，验证了有限元仿真的正确性，为冷滚打成形高精密工件提供了参考。